大家好,欢迎来到IT知识分享网。
漫谈Fermat小定理
费尔马(Pierre de Fermat,公元1601年—公元1665年)是个多产的数学家,本职工作是公务员,被称为最伟大的业余数学,但一般认为,即使是顶尖的职业数学家,也未必比得上他.

他最伟大的贡献就是那个迷惑人类358年的大问题:
著名的费尔马-怀尔斯定理是说:
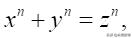
当 n 大于 2 时没有正整数解。
这个问题的解决是相当相当的困难(参见《费马大定理―一个困惑了世间智者 358 年的谜》
作者:西蒙·辛格)。

由费尔马大定理的一个简单的应用:
我们用直尺和圆规在平面上不能画出
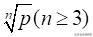
,p为质数。
除此以外,费尔马的贡献多而杂,几乎涉猎当时数学的所有领域,比如:导数与切线,最小极值点,方程与曲线,概率与统计。对了,还有著名的费尔马小定理:
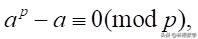
其中p是一个素数,a是正整数。
也可以用整除的形式来写:
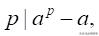
事实上它是Euler定理的一个特殊情况,Euler定理是说:
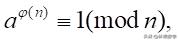
a,n都是正整数,φ(n)是Euler函数,表示和n互素的小于n的正整数的个数。
大家可能不爱Euler函数,但爱Euler复数啊!
不只是小伙子爱它,姑娘也爱它!
费尔马小定理为什么在数论中比较重要,这是因为它是数论中仅有的两个素性判定定理之一,另一个是威尔逊定理(Wilson’s Theorem),即:
当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p ),
实际上这个定理最早出现在莱布尼兹( Leibuitz) 的研究中,它给出了判定一个自然数是否为素数的充分必要条件。但是由于阶乘是呈爆炸增长的,这个计算量不是一般的大,甚至比古老的筛法计算量还要大,那么谁还会用这个方法去判素呢?
现在一个最为古老也是最为困难的问题是表质公式,如果不计时间的话,下面的“表质公式”就可以求出所有的质数:
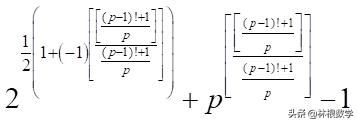
其中的[ ]表示高斯函数,这样计算出的结果全部是质数,不信你试试?
费尔马小定理难证吗?如果要用同余理论的话,也不是太难,只是需要一些七七八八的引理,比如二次剩余什么的,为简单易懂,说一下大意喽!
比如:
任意取一个质数,比如11。考虑从1到10的一系列整数1,2,3,4,5,6,7,8,9,10,给这些数都乘上一个与11互质的数,比如3,得到3,6,9,12,15,18,21,24,27,30。对于模11来说,这些数同余于3,6,9,1,4,7,10,2,5,8。这些余数实际上就是原来的1,2,3,4,5,6,7,8,9,10,只是顺序不同而已。
把1,2,3,…,10连乘,乘积就是10的阶乘10!。把3,6,9,…,30也统统乘起来,并且提取公因子3,乘积就是
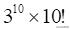
对于模11来说,这两个乘积都同余于1,2,3,…,10系列,尽管顺序不是一一对应,即312×10!≡10!(mod 11)。
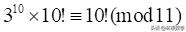
两边同时除以10!得
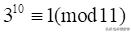
如果用p代替11,用a代替3,就得到费马小定理
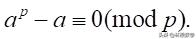
怎么样,这个证明还算简单吧?
如果不认识同余呢,也没有关系啦,总知道数归吧,就是那个多米诺骨牌效应的数学归纳法

,以下用数归的方法证之(这里对a进行数归,无法对p数归,因为p不具有连续性),但需要注意,用数归的第一步是验证a=1,2时成立,然后假设a=k成立,最后再推出a=k+1时也成立,有时会说a=1时显然成立,这里是a=1显然成立,但a=2也是显然的吗?有一点重要的是,这里的a=1成立,有它的特殊性(值为0),那么a=1到a=2的递推,与a=2到a=3的递推便有本质的不同,
既然a=2,并不显然,那就证一下呗:
a=2时,
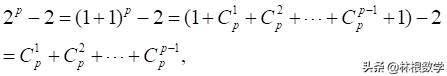
由于P是质数,显然
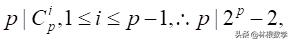
则知a=2命题成立;
假设a=k时,命题成立,即
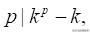
则有
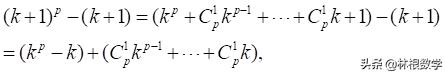
由上述假设
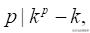
且易见
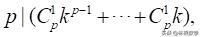
则知
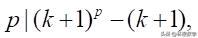
此表明,当a=k+1时命题也成立,由归纳原理知,命题对所有的自然数a都成立.
应用组合论,Fermat小定理还有如下的证法,这种证法可以想象为项链证法:

设有n种不色的珠子,每种珠子的数量充分,我们先将这些珠子串连成由p顆珠子组成的一切可能的直串.然后把这些直串两头联结起来成为项链,用这种方法得到的项链中,有多不同的.也有许多是一模一样的.现在计算各种不項链的条数。
首先把一条直串围成一条項链.从上向下围和从下向上围.珠子的循环次序恰好相反(如图1)
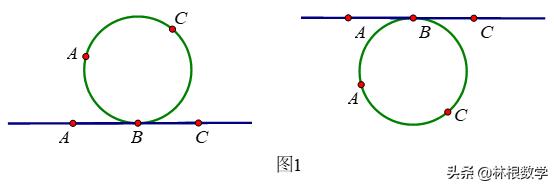
如一条项链经过旋转得到时另一项链,么这两条项链显然是一样的。但是,如果一条項链一定翻过身才能旋转成另一条,那么项链(如2),就不算是一样的·
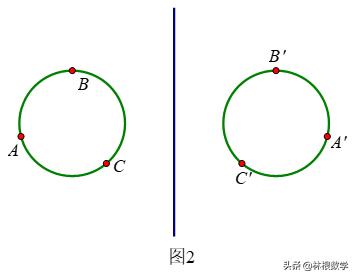
由于直串围成項链的方式不,所得到的項链也不同,所以我们规定所有的直串围成項链必须采取同样的方式,比如,一律从下往上围或从上往下围。因为一条直串的p颗珠子中的每一颗都可以选择n种不同的颜色。所以总共有
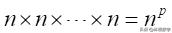
条不同的直串,p顆珠子组成的单色項链共有n条,每条这样的項链经过旋转不会产生变化,除去这n条单色的。还剩下
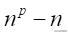
条多色直串.只有它到围成項链才有可能出现同样的.
任取一項链N,如果把这項链依次在相邻两珠之间的p个位置处切断,那么我们就得到直串
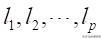
(如图3,弧上的短线表录切口)
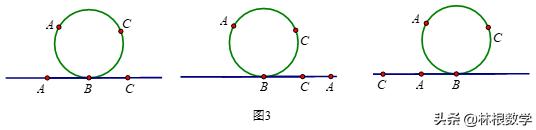
現在,我们明这些串是互不相同的,如若不然,有两条
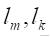
是相同的.与这些直串应的切口
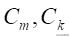
之间的个数为d(如图4)
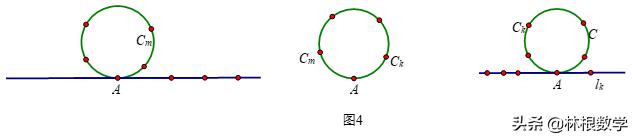
如果把一条N式項链重在另一条N式項链上,使上下珠子的颜色完全一致.再让上面的項链转过d颗珠子,使上方的切口与下方的切口重合
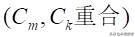
那么由于
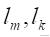
完全一样.所以上下的珠子仍然完全相同。
由此可見,在N項链上,转过d颗珠子不会改变其上珠子颜色的搭配.因比,在項链N上,每顆珠子都一定和自它开始转过d颗珠子后的那珠子相同,如果d=1,所有珠子都有相同的颜色,这种单色項链不在考虑之列。所以d>1,又由于d是两个切口之间的珠子的个数,故d
由于p是素数,1
因此項链N上每隔r-1颗珠子的色必定一样.由于N不是单色項链.所以r≠1,即1
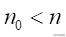
具有相同的的性质,重复这种论证就会推出:有无多个整介于1与p之间,这走不可能的.于是们证明了p个直串
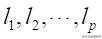
是互不相同的.
这样一来,在直串与项链之间存在着p对1的对应,就是说p条不同的直围成的P条项链实际上是同样的项链,因此,不同的项链是
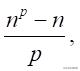
这个既然是整数,所以
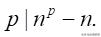
证毕.
说明:本文的最后一种证法引自《Fermat定理的若干再证明(续)》(陈艳凌,祝微,长春师范学院学报,自然科学版,2006,10)
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/144054.html

