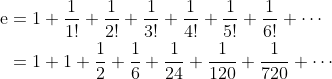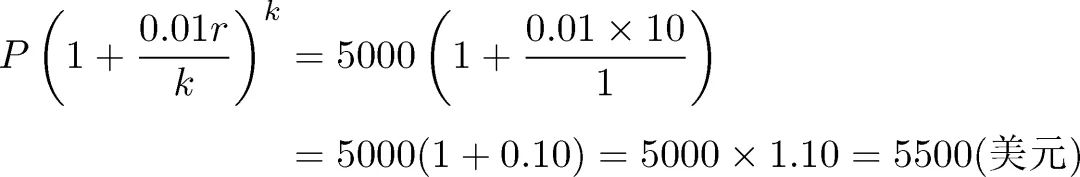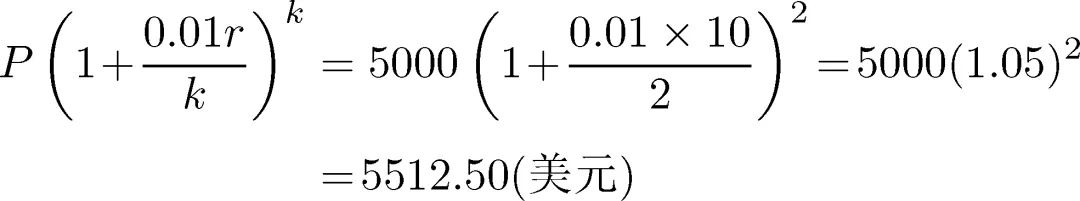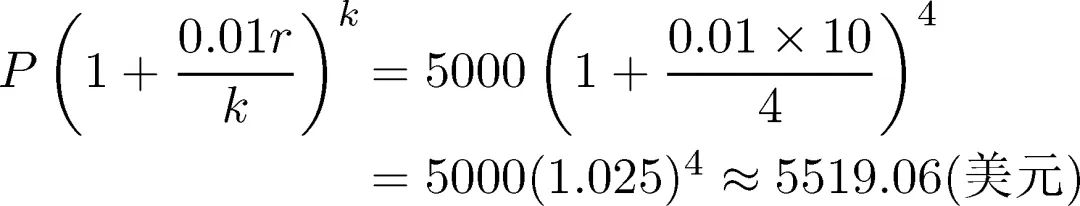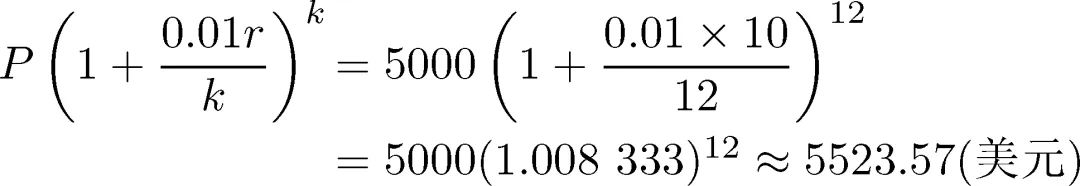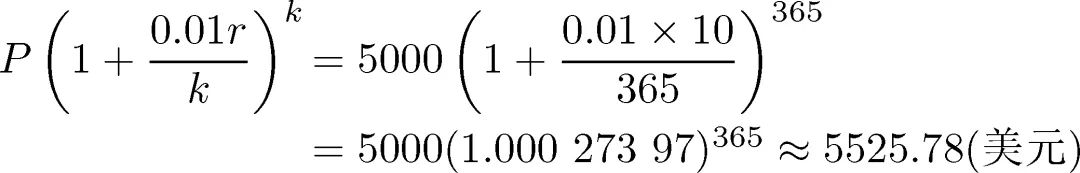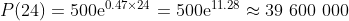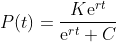大家好,欢迎来到IT知识分享网。
我们要讲一个特殊的数, 这个数记作e, 以及它永恒的伴侣自然对数的故事。乍看起来, 它们既不特殊也不自然。相反, 直觉告诉我们它们似乎没有什么意义。我们的目标是解释其中的原因, 而此时直觉是错误的。
来源 | 《数学那些事:伟大的问题与非凡的人》
作者 | [美] 威廉·邓纳姆(William Dunham)
译者 | 冯速
我们先从e开始。当然, “e”是英语字母表中的第五个字母, 但是数学家的e是一个实数, 其十进制表示为


在回答这个问题之前, 我们必须解释e是如何定义和计算的, 也就是它是从哪里来的。它有两个来源, 但它们是逻辑等价的, 一个是极限, 一个是无穷级数。首先我们讨论极限定义模式。
考虑下面的表达式
其中

如果
如果
等等。数学家总是准备着把某些事情推到极限, 设
用语言表述就是, e是表达式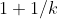

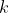
显然, 
再稍稍做一些工作就可以证明更一般的结果:
公式A
在上面的公式中, 当我们取
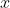

生成e的第二个方法是求下面无穷级数的和
其中, 分母是我们在第B章中介绍过的阶乘。在这个级数中加入越多的项, 我们就越靠近e的值。
当然, 这两个生成e的公式看起来差异很大。然而, 可以证明
因此, 估测下面式子的值是很有启发意义的
这个和是2.718 281 83,这是由上面的极限定义的e的一个相当精确的近似值。
于是, 使用这种级数的方法, 我们可以求e的任意次幂, 换句话说, 对于任意的

公式B
例如, 为了估测


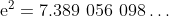
在数学史中, 与这个e关系最密切的人就是莱昂哈德 • 欧拉, 我们已经在第E章中遇到过他, 在本书的其他地方我们还会遇到他。正是欧拉为这个常量选择了这个符号, 也是他领会到了这个常量的重要性。图N-1重现了他在1748年发表的论文《无穷分析引论》中的一段, 我们看到欧拉引入了我们刚才所说的公式B, 但他写的是

我们已经描述了定义和计算这个特殊数的两种方法。但是为什么还要烦恼呢?它为什么重要呢?它为什么又是自然的呢?正如我们将看到的那样, 它的用途几乎无穷无尽。
一个应用就是银行存款利息增长问题(这是一个与我们所有人都有关系的话题, 大家都希望存款利息变多)。确定复利的公式说的是, 如果我们在年利率为
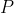


这就是银行家知道并喜爱的结果。
举一个例子, 假设我们在投资回报利率为


好的。但是, 假设这家银行决定如下分段分配利息:不是一年只给

在上面的利息公式中, 除了现在

这个投资回报稍微好些。
一个想法慢慢浮现。如果这家银行更频繁地支付利息, 比如一个季度、一个月或者每天, 那么我们也许会得到更多的好处。为了做一下研究, 在各种利息方案下, 计算一下我们的钱数总额:
按季度复利, 我们设
这个结果相当好。下面是按月复利计算, 此时
这个结果更好。下面再按天复利计算(
流着贪婪的口水, 我们设想着这家银行不是按日复利计算而是按小时、按分钟, 甚至是按秒。事实上, 为什么不设想所有可能的利息计算中最好的情况, 即连续地计算复利利息?这样我们就不必为下一次利息支付哪怕等待一毫秒。我们设想着把
形式上, 说复利计算是连续的, 意思是我们设复利周期数

其中

对于我们的例子来说, 在一年按

这是在年利率为
在确定银行存款的连续增长中e非常有用, 无须惊讶, 在其他连续增长类问题中它也会出现。例如, 种群增长(可以是人口数量或者是细菌数量)可以看成连续增长, 人口出生率与现有人口成正比。这样的理论是英国经济学家托马斯 • 马尔萨斯于1798年提出来的, 用来解释人口增长。半个世纪后他的著作被另一位科学家引用, 这个人就是杰出的查尔斯 • 达尔文。[2]
在这样简单的人口模型下, 时间
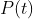
其中, 

举一个例子, 我们从有盖培养皿里的



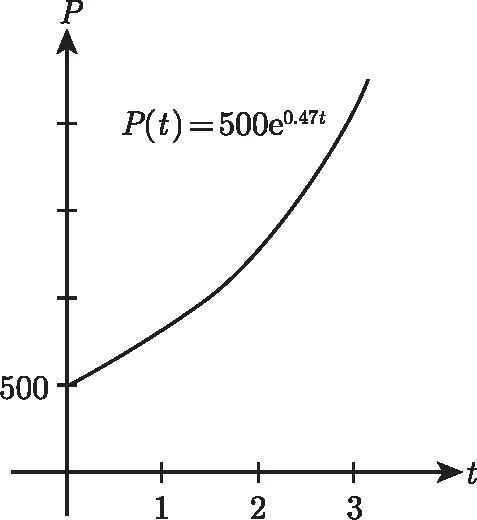
图N-2给出了它的图像。注意, 对于小的时间值

图 N-2
更具体地说, 在

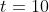

如果这个过程不受限制, 持续一周, 此时将有的细菌数是
这肯定会导致一场流行病。这些数字和它们陡峭上升的图像显然说明细菌数呈“指数增长”。
然而, 在这一推理过程中很容易发现一个不足之处, 因为无论是人口数量还是细菌数量都必须有一个上限。最终细菌会用尽食物、水或空间。因此, 没有限制的增长是不切实际的增长。
因此, 数学家们改进了他们的方法, 考虑了在人口增长过程中固有的限制条件。其中有一个改进后的模式称为逻辑斯谛(logistic)模型, 它导致这样的一个方程:
其中, 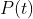
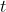

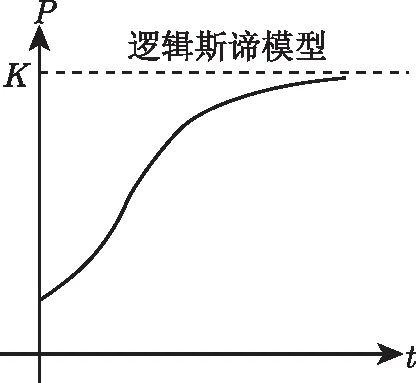
图N-3给出了一条逻辑斯谛增长曲线。对于较小的时间

图 N-3
当然, 我们掩盖了关于这些方程的起源的诸多技术点。另外, 生物学家甚至设计了更玄妙的模型来反映自然状态中的人口行为。(例如, 如果抗生素进一步限制了细菌的增长, 将会发生什么?)然而, 对于我们的目标, 其中重要的一点是人口增长依赖于数e。它很自然地描述了我们周围的生物世界。
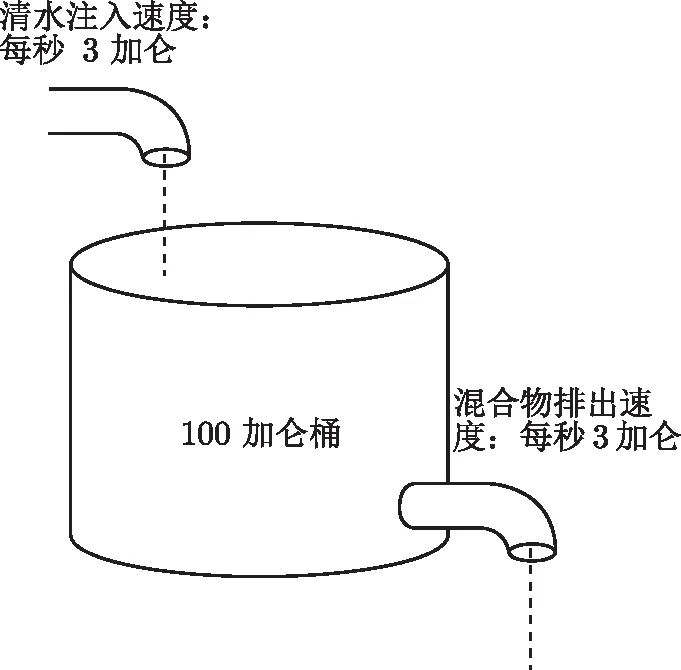
很多其他现实生活的情况也与这个数e不期而遇。考虑下面这样一个事例:一位硫酸制造商有一个100加仑的大桶, 其中装满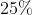

图 N-4
显然, 这个过程将不断地稀释大桶中的混合物。而且显然这种情况的精确动态远不是这样简单。注入的水并不会单纯地取代酸。相反, 被注入桶内的一些清水正作为混合物的一部分被排出桶外, 而同时一些酸却保留在溶液中。制造商所面临的问题是如何确定在冲洗过程进行了
这个问题的分析要借用积分技术, 它产生了下面的

在这个方程中e的重要性再一次充分地显示出来。
我们再具体看一下这个方程。开始时, 这只大桶里装有

过了1分钟, 酸浓度变成
如果这位制造商继续这个过程15分钟, 即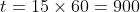
总之, 15分钟后这只大桶基本已经被冲洗干净了。
如果我们回想一下第B章中讲述的雅各布 • 伯努利的工作, 就会明白我们是在不同的环境下遇到了e。在那里, 我们看到投掷一枚均匀的硬币500次后正好得到247个正面的概率是由下面这个令人恐惧的公式给出的:
这种概率计算是不可能直接进行的。但是, 利用一点数理统计的知识, 就可以知道这个概率的近似值可以由下面的式子给出
上式中的e因某种看似无法解释的原因再一次起着重要的作用(

因此, 在数学中e的意义极其重大, 在理论与实践中都起着重要作用。当我们冲洗大桶或者投掷硬币时它存在, 当我们赚取利息或者观察细菌繁殖时它也存在。颇像狄更斯小说中的人物, e一直在最意想不到的地方出现。但是, 狄更斯笔下人物的出现或再现都要求读者接受这样的假设, 即无论多么不可能的事都在情理之中, 而e的出现和再现只要求我们对数学稍稍有些了解。
然而, 这只是这个故事的一半。发现e的威力很重要, 但是把这个过程反过来同样很重要。考虑下面的例子。在把




但是, 如果我们知道



我们的“援救”是“逆指数”过程, 它撤销

它的一个重要性质是下面的反演公式:
在符号形式下, 它说明了我们上面用语言所表达的意思:自然对数撤销指数运算, 即如果我们开始用








但上面的关系告诉我们

概括起来:数学家经常要另辟路径, 不是从



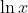
午夜时分, 警察被召集到一个血迹斑斑的谋杀现场, 在那里他们发现埃迪(绰号“黄鼠狼”)的尸体, 他是个惯犯, 跟黑社会有关系。到达现场之后, 警员们注意到当时气温是适中的


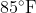

根据一条秘密消息, 警察抓获了克莱尔, 她是埃迪的梦中情人。克莱尔在路易斯酒吧里度过了一个晚上, 喝得多了点, 可能威胁过埃迪的生命。晚上11:15, 她怒气冲冲地离开了。这似乎是一个很清楚的案件。
幸运的是, 克莱尔知道自然对数。她还知道牛顿的物体冷却法则, 这是热量消耗理论的基础。牛顿法则说的是一个物体的冷却速度与它的温度和它周围的温度之差成正比。用我们日常的话来说就是, 一个物体比空气温度高得越多, 它的冷却速度就越大, 所以它会迅速变冷;当它比周围环境热得不多时, 它的冷却速度就小, 因此它就慢慢地变冷。
牛顿法则适用于任何正在变冷的物体, 无论是刚出烤箱的热乎乎的土豆, 还是躺在人行道上的尸体。活人是不会变冷的。新陈代谢确保人类的体温维持在98.
把上面的语言描述转化成简练的数学公式并利用微积分, 克莱尔导出了下面的方程
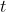
再一次注意到e的出现。利用计算器, 你可以验证在午夜, 即
这正是警察刚到达时确定的体温。同样在凌晨2:00时, 即当
这个数字再一次验证了警察的观察。换句话说, 这个公式在我们实际拥有的这两个数据上都运作得很好。
但是, 克莱尔要面对的最关键的挑战是确定最后遇到埃迪的时间。她必须利用这个公式反推这个冷却过程, 从而计算当埃迪的体温是正常体温

所以, 我们把人类正常体温的
把上面方程两边减去


我们的目标是求
此时, 因为

因此在时间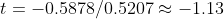

这里的

在审判时, 克莱尔的律师一一介绍了上面的证据, 非常有说服力地引用了“自然法则和自然对数”, 在由数学方面十分老到的人们组成的陪审团面前赢得了无罪的宣判。要感谢自然对数, 它维护了正义。
法医一定知道自然对数。遗传学家、地质学家以及那些研究动态现实世界现象的每一个人都知道自然对数。撇开直觉, 它是一个非常重要、非常普遍的有用思想。我们相信, 在考虑了上面证据的基础上, 本书的读者陪审团将裁决数e和它的另一半, 即自然对数, 虽被人们严重忽略, 但其自身并无过失。
推荐阅读
《数学那些事:伟大的问题与非凡的人》
作者:[美] 威廉·邓纳姆(William Dunham)
译者:冯速
看完顿感舒爽,让数学课堂上的知识变得更好懂、更通透;无需动用纸笔,纵览数学世界不可不谈的伟大定理、难题和争论;好奇心大满足,纵览数学的核心知识和历史八卦。
本书是一部短文集,文章以各自英文标题的首字母按照A到Z的顺序排列,每一篇短文都讲述了一个特定的数学主题,介绍了数学世界不可不谈的伟大定理、难题、争论和不解之谜。作者以简单清晰的笔触,带领读者跨越历史,探索算术的起源、圆的奥秘、无穷级数的难题、无理数的怪异特征等话题,讲述了数学大师们的生活轶事和神秘经历,勾勒出数学的概貌。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/144205.html