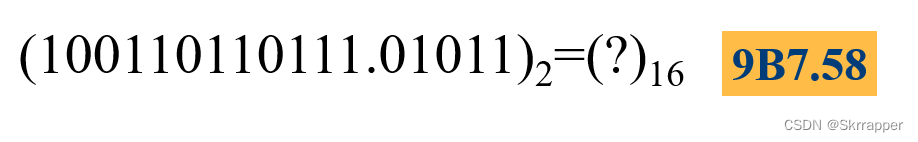进制的基本介绍以及进制转换和计算

大家好，欢迎来到IT知识分享网。

我们知道，计算机使用的是二进制来存储信息。而在我们现实生活中，一般是用十进制来表示一系列数值。同时在更加精细的领域还存在着像八进制，十六进制等等一些进制。那么进制究竟是什么？不同的进制之间又是如何实现转换的？接下来我来详细介绍一下。

一、进制是什么？

进制即是进位计数制。是用一组固定的符号和统一的规则来表示数值的方法。生活中常见的进制有十进制、二进制、八进制、十六进制。
在计算机中，数据都是以二进制形式存储的。
进制主要包括三个部分：数位、基数、位权

数位

指数字符号在一个数中所处的位置。

我们平常说的个位数十位数等等，就是数位的概念。

基数

是一种进位计数制允许使用的基本数字符号的个数。

位权（简称“权”）

是指数制中每个固定位置对应的单位值（常数）。

例如十进制的123，1的位权是100，2的位权是10，3的位权是1。
二进制的110，从右往左，0的位权是2的零次方，第一个1的位权是2的一次方，第二个1的位权是2的二次方。
所以从二进制中可以看出，位权其实是以数字符号所处位置的序号为指数的整数次幂。
在十进制中，位权是10^n
在二进制中，位权是2^n
…

二、常见进制介绍以及之间的转换

1.表示

一般情况下，在数字后面用特点的字母（下标）表示该数的进制
二进制；B
十进制：D（可以省略O）
八进制：O
十六进制：H
同时也可以用数字后面加进制来表示。

2.限制

十进制的每位数字的范围：0~9
二进制的每位数字的范围：0~1
八进制的每位数字的范围：0~7
十六进制的每位数字的范围：0~F（f）

3.转换

其他进制数转十进制数

十进制数转其他进制数

整数部分：除二取余法
原理：任何一个数除以2得到的余数都是0或1
例如（十转二）：

小数部分：乘二取整法
原理：当小数与2相乘时不可能大于1。
例如：

二进制数转八进制数（十六同理）

以小数点为中心，整数部分自右向左每3位一组，最后一组不满3位时补0；小数部分自左向右每3位一组，最后1组不满3位时补0。
举例：

注意这个例子中小数部分最后是不满3位的，所以要补0成为110。

转十六进制数即是将每3位改为每4位。
举例：

同理小数部分不满4位，所以要补0成为1000。

八进制数转二进制数（十六同理）

即：将二转八反过来，将1位八进制数转换为3位二进制数即可。
举例：

各种进制数码对照表

实际上只要对照表格即可知道对应的关系，就相当于数学中的乘法口诀表一样，熟记于心即可快速转换。

4.基本运算

加法：

举例

减法：

举例：

乘法：

举例：

除法：

举例：