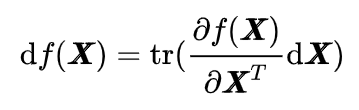大家好，欢迎来到IT知识分享网。
目录
本篇博客总结自知乎文章：矩阵求导公式的数学推导（矩阵求导——进阶篇），需要详细推导过程可以查看原文学习。
文章主要介绍了矩阵迹的性质，并将矩阵微分引入到矩阵求导中。虽然在法则和公式中涉及到了矩阵变元的实矩阵函数，但是并不介绍如何求导实矩阵函数，只介绍矩阵变元的实值标量函数利用微分求导的过程（实矩阵函数的求导过程远比实值标量函数的求导过程复杂）。
一、矩阵的迹
1. 迹的定义
对于一个 
的方阵 ：
它的主对角线元素之和就叫做矩阵 的迹(trace)，记作：
2. 迹的性质
2.1 标量的迹
因为标量可以视为 的矩阵，所以对于一个标量 ，它的迹等于它本身：
2.2 转置的迹
因为转置并不改变主对角线元素位置，所以对于一个矩阵 的转置 ，它的迹与原矩阵相等：
2.3 乘积的迹
矩阵 与矩阵 的乘积的迹，等于两个矩阵对应位置的元素相乘再相加，类似于向量内积的延伸：
2.4 迹的交换律
由上一性质可知，在两矩阵交换位置后，乘积的迹不会受到影响，仍然是对应位置元素相乘再相加，即满足交换律：
对于多个矩阵相乘，可以将其中一部分矩阵视为整体，然后使用交换律：
不仅如此，迹的矩阵交换不变性还可以和迹的矩阵转置不变性结合，得到如下转换过程：
2.5 迹的线性法则
矩阵先相加再求迹，等于先求迹再相加：
二、微分与全微分
1. （全）微分的表达式
高等数学中的一元函数的微分表达式与多元函数全微分表达式如下：
|
函数类型 |
参数说明 | 表达式 |
|---|---|---|
|
普通一元函数 |
|
|
|
复合一元函数 |
|
|
|
||
|
普通多元函数 |
|
|
|
复合多元函数 |
|
|
|
2. （全）微分的法则
无论是一元函数的微分还是多元函数的全微分，都遵循以下四个法则：
| 法则 | 参数说明 | 表达式 |
|---|---|---|
| 常数的微分 | 为常数 |
|
|
||
| 线性（加减）法则 | |
|
|
||
| 乘积法则 | |
|
|
||
| 商法则 | |
|
|
|
三、 矩阵的微分
1. 矩阵微分的实质
对于一个矩阵变元的实矩阵函数，其内部的每一个元素就是一个矩阵变元的实值标量函数：
|
|
|
|---|---|---|
 |
||
| 对其求微分就是对每个位置上的元素求全微分，排列布局不变； | ||
 |
||
2. 矩阵微分的意义
对矩阵变元的实值标量函数，其全微分可以转化为如下迹的形式：
- 其中左边的矩阵就是对
的分子布局形式求导：
- 而右边的矩阵就是 的全微分：
所以矩阵变元的实值标量函数的全微分可以表示为：
3. 矩阵微分的法则
因此，我们想要求解一个矩阵变元的实值标量函数的导数，我们只需要把该函数转化成上面的形式。而转化的过程可以通过下面矩阵微分的四个法则实现：
| 法则 | 参数说明 | 表达式 |
|---|---|---|
| 常数矩阵的微分 | 常数矩阵 |
|
| 线性法则 | 常数 |
|
| 乘积法则 | |
|
|
||
| 转置法则 | |
|
4. 矩阵微分的常用公式
对于转化过程中经常出现的矩阵形式，我们可以记住下面三类常用公式来简化推导步骤，这些公式也是由矩阵的微分四法则结合矩阵的迹的性质得来：
| 公式名称 | 参数说明 | 表达式 |
|---|---|---|
| 夹饼层 | 常数矩阵 |
|
| 将 替换为矩阵函数 |
|
|
| 行列式 | |
|
| 将 替换为矩阵函数 |
|
|
| 逆矩阵 | |
|
|
将 |
|
四、矩阵求导实例
1. 迹在微分中的应用
对实值标量函数 ，由于它的结果是标量，所以有：
上式结合微分的线性法则（相加再微分=微分再相加）：
若把实值标量函数 视为实矩阵函数 的迹：
则有：
2. 利用微分求导
举例说明如何利用矩阵微分，推导出矩阵求导的表达式：
结合矩阵的迹的性质、矩阵微分的四个法则和六个常用公式，推导过程如下：
| 迹在微分的应用 | |
|
|
| 夹饼层公式 | |
|
|
| 微分乘积法则 | |
|
|
| 迹的线性法则 | |
|
|
| 微分转置法则 | |
|
|
| 迹的交换与转置 |
|
|
|
|
| 迹的线性法则 | |
|
|
最终得到该式的微分：
结合公式：
可得导数：
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/147303.html
