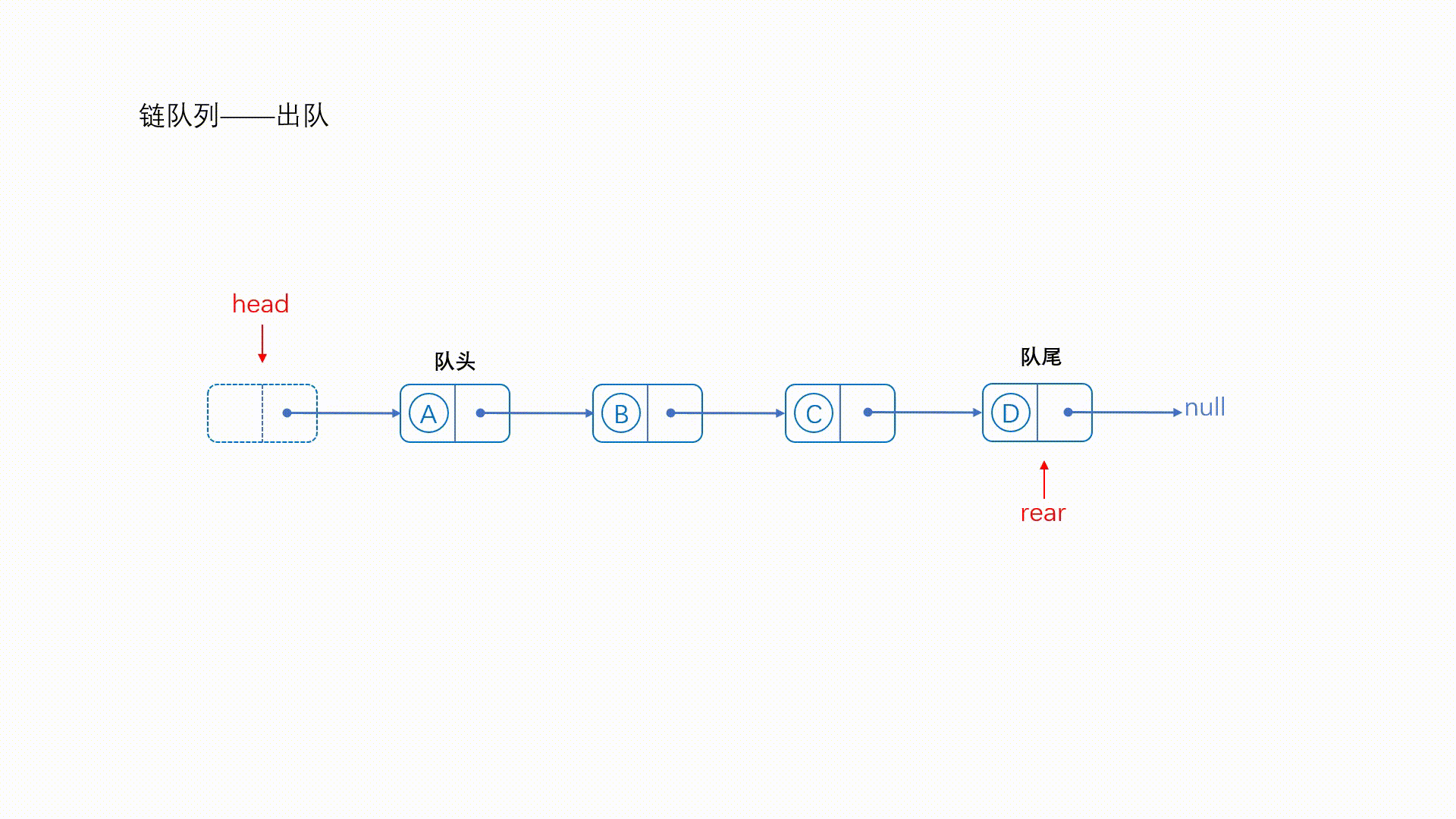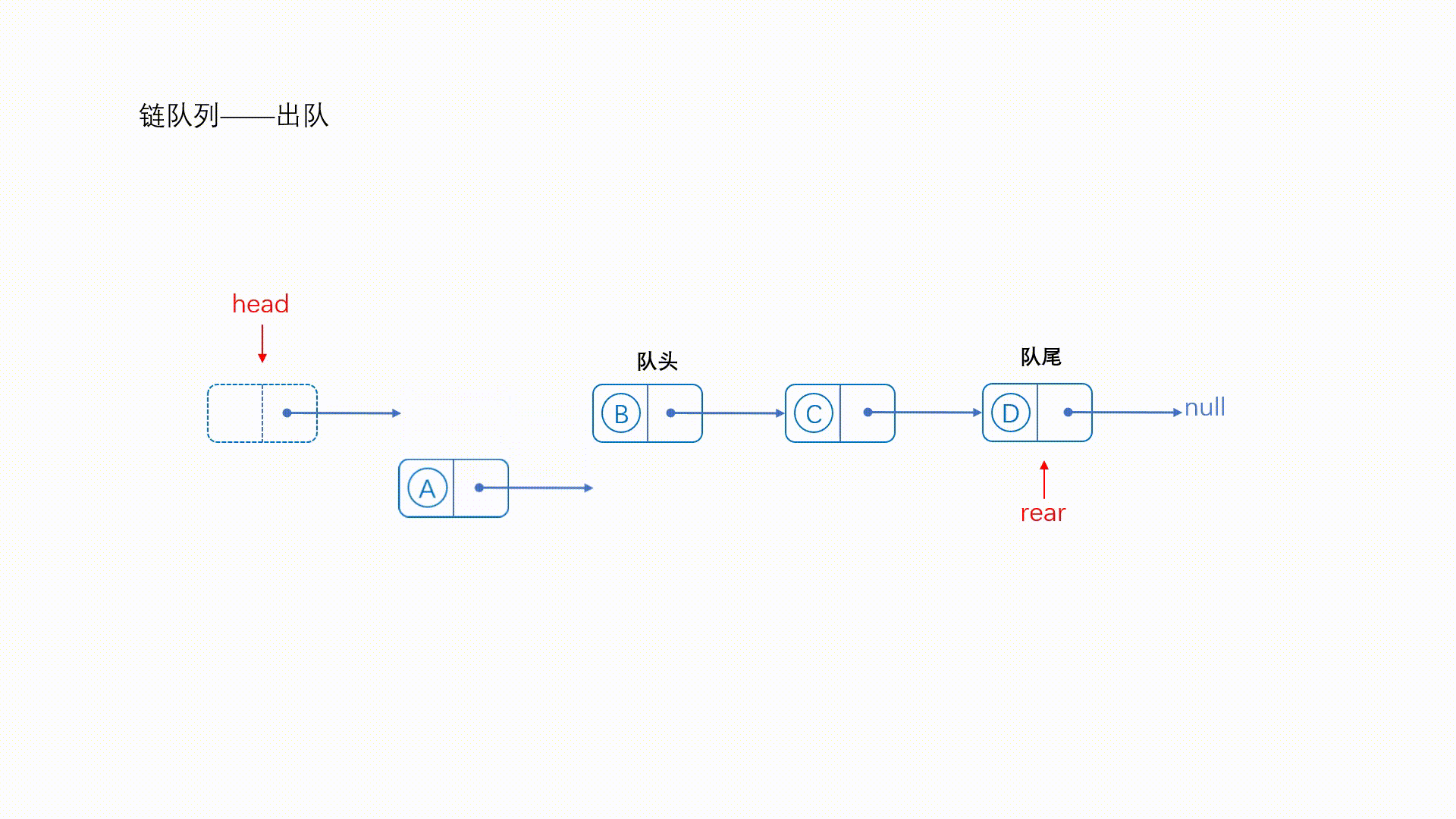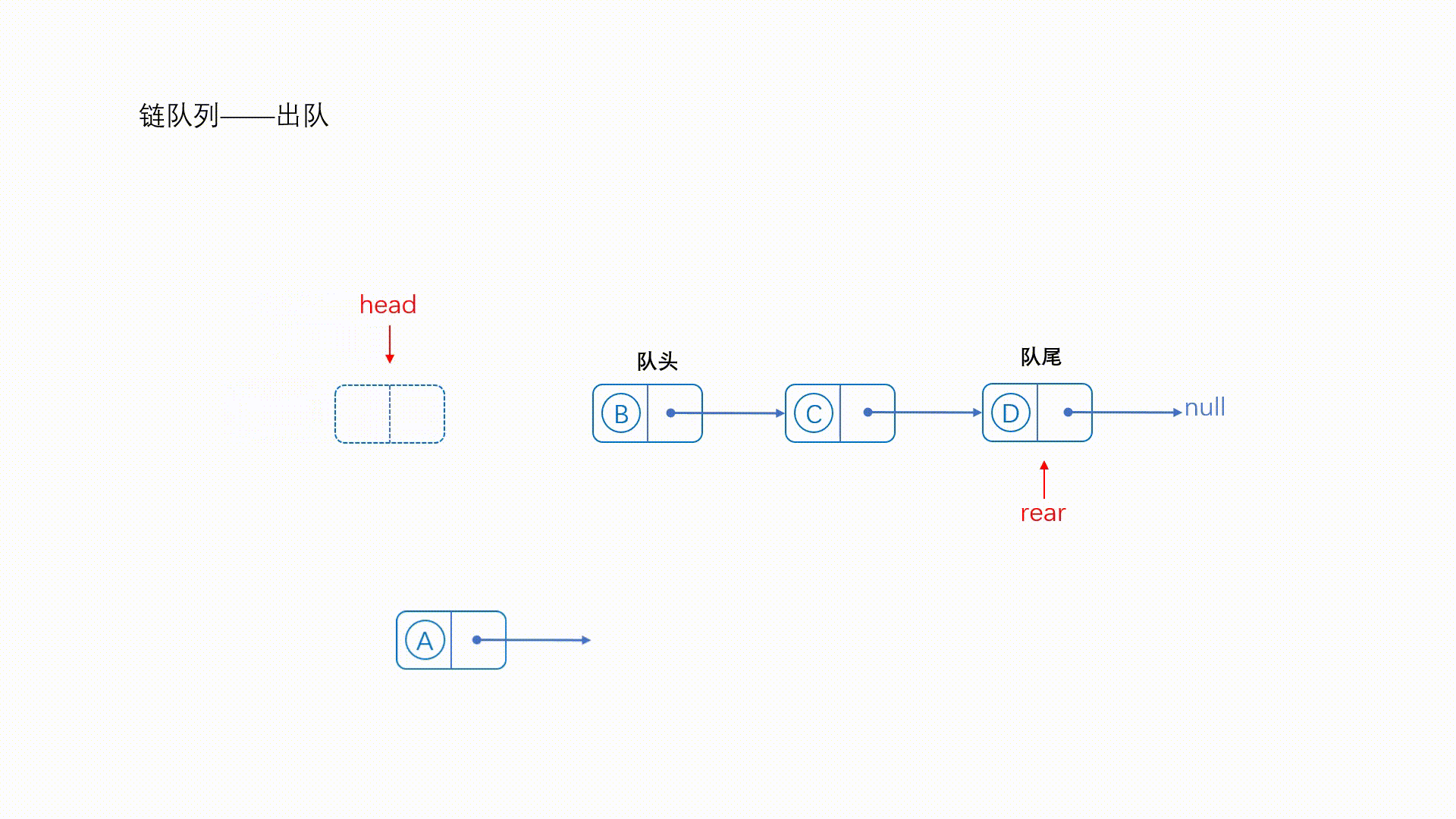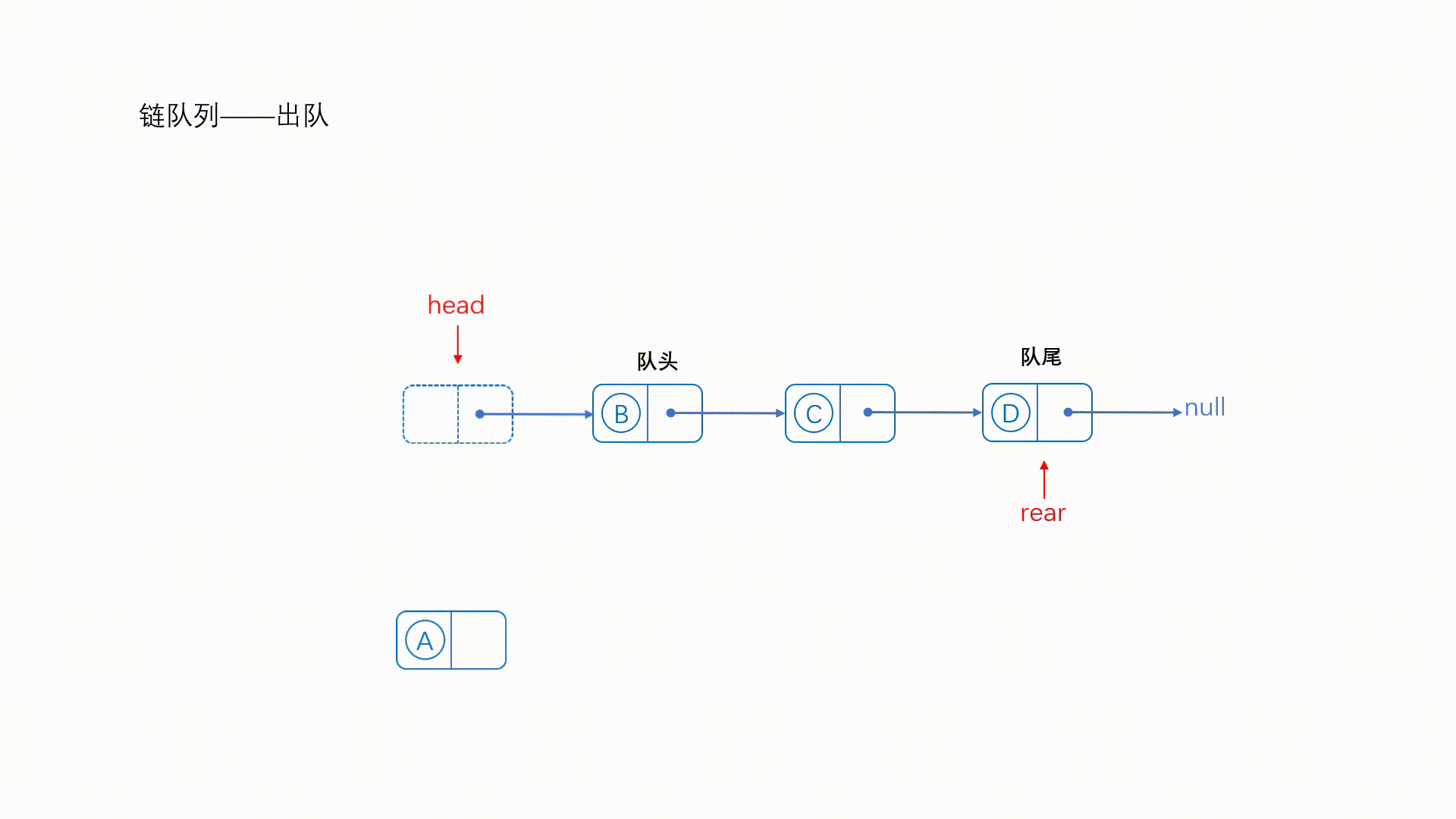【数据结构】栈与队列：后进先出与先进先出到底是啥？

大家好，欢迎来到IT知识分享网。

• 👑专栏内容：数据结构
• ⛪个人主页：子夜的星的主页
• 💕座右铭：日拱一卒，功不唐捐

一、前言

栈和队列是两种常见且重要的线性数据结构，它们在解决各种实际问题和算法实现中发挥着关键作用。本文将详细介绍栈和队列的概念、特点以及各自的应用场景。我们将从生活中的例子出发，形象地解释栈和队列的工作原理，也会使用不同的数据结构实现栈和队列，以及它们的优缺点。

二、栈的概念

1、定义

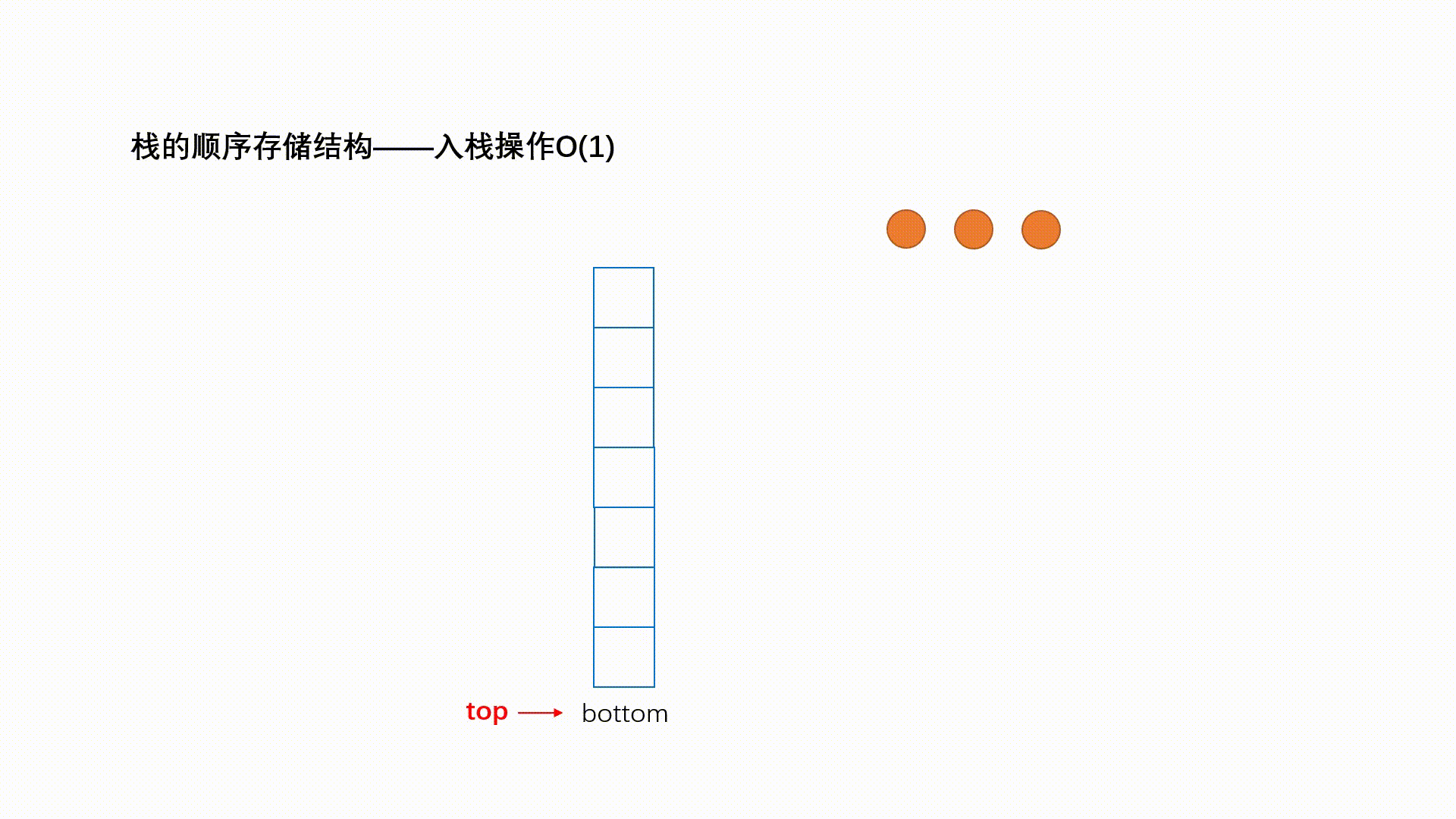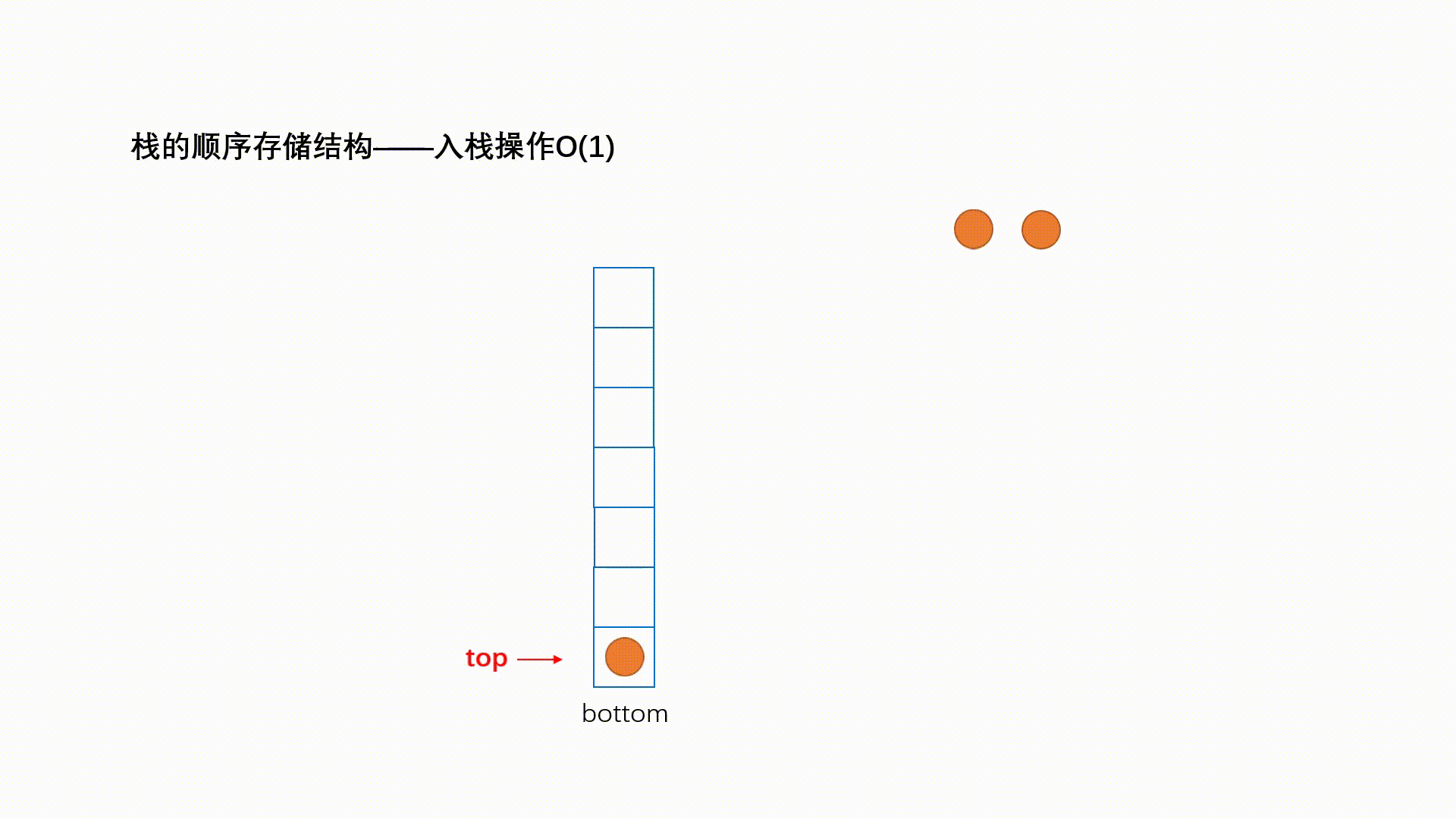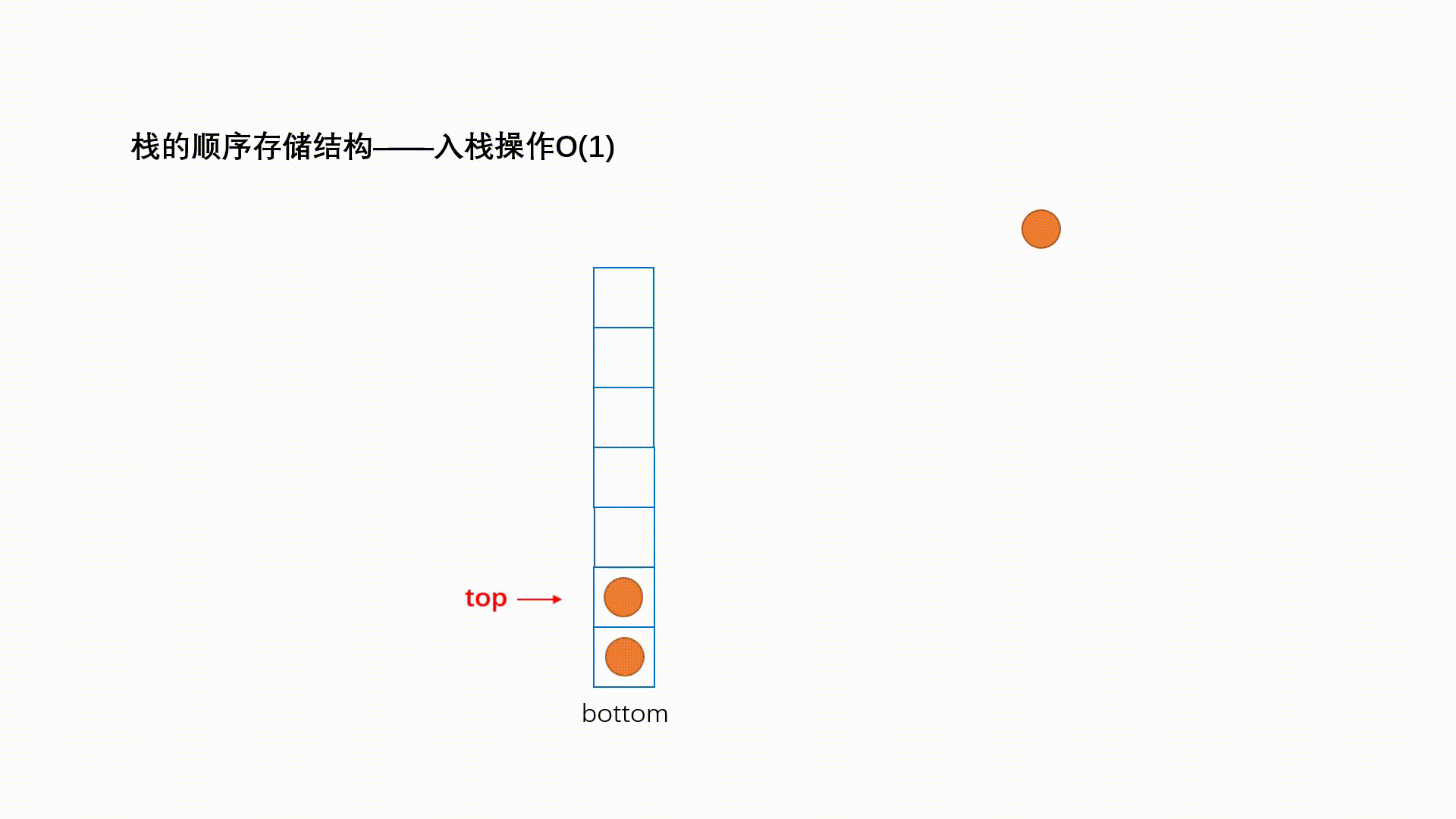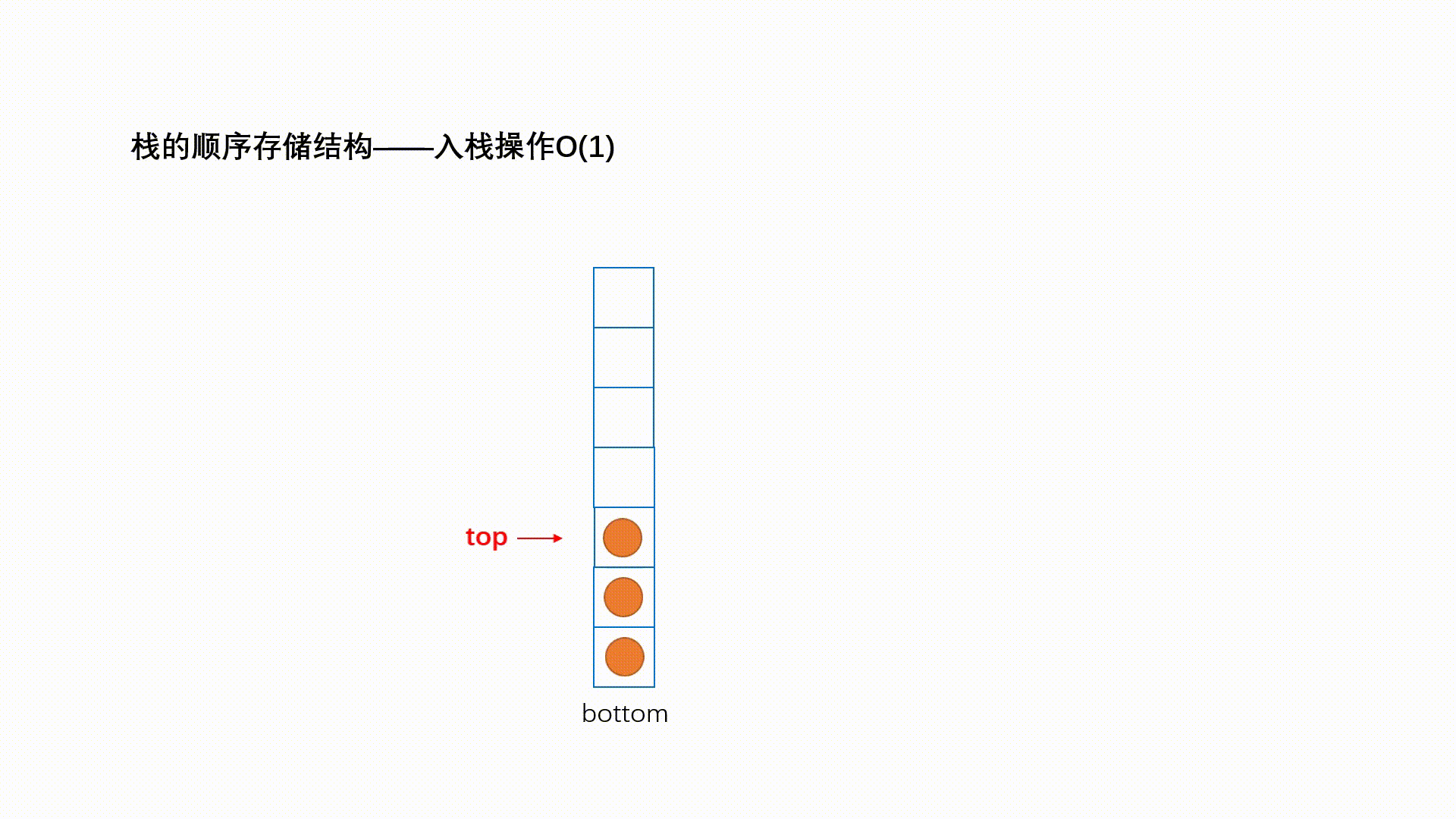
栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

我们可以简单的把栈形象地看成一筒羽毛球，当往筒里放球时，球从筒底排到筒口，当从筒里拿球的时候，球从筒口往下依次被拿出来，直到筒底的最后一个球被拿出来。

2、操作

通常对栈执行以下两种操作：
向栈中添加元素，此过程被称为”进栈”（入栈或压栈）；
从栈中提取出指定元素，此过程被称为”出栈”（或弹栈）；

三、栈的实现

1、定义

typedef struct Stack { 
    int *data; //（1） int size; //（2） int top; //(2) }Stack; 

（1）用来存储数据的数组
（2）用来表示线性表的最大存储容量的值
（3）用来标识栈顶元素的栈顶下标

2、栈的初始化

Stack *initStack(int n) { 
    Stack *s = (Stack *)malloc(sizeof(Stack)); s->data = (int *)malloc (sizeof(int)*n); s->size = n; s->top = -1; return s; } 

为什么栈顶的下表要初始化为-1 呢？

3、栈的销毁

void clearStack(Stack *s) { 
    if(s ==NULL) return ; //（1） free(s->data); //（2） free(s); //（3） return ; } 

（1）如果栈为空，直接返回
（2）销毁存储的数据
（3）销毁栈

4、栈的判空

int empty (Stack *s) { 
    return s->top == -1; } 

5、查看栈顶元素

int top(Stack *s) { 
    if(empty(s)) return 0; return s->data[s->top]; } 

6、入栈与出栈

Ⅰ、入栈

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

int push(Stack *s,int val) { 
    if(s->top + 1==s->size )//（1） return 0; s->top = s->top+1; //（2） s->data[s->top] = val; //（3） return 1; } 

（1）如果栈已满

（2）栈顶指针向上移动

（3）将数据让如栈中

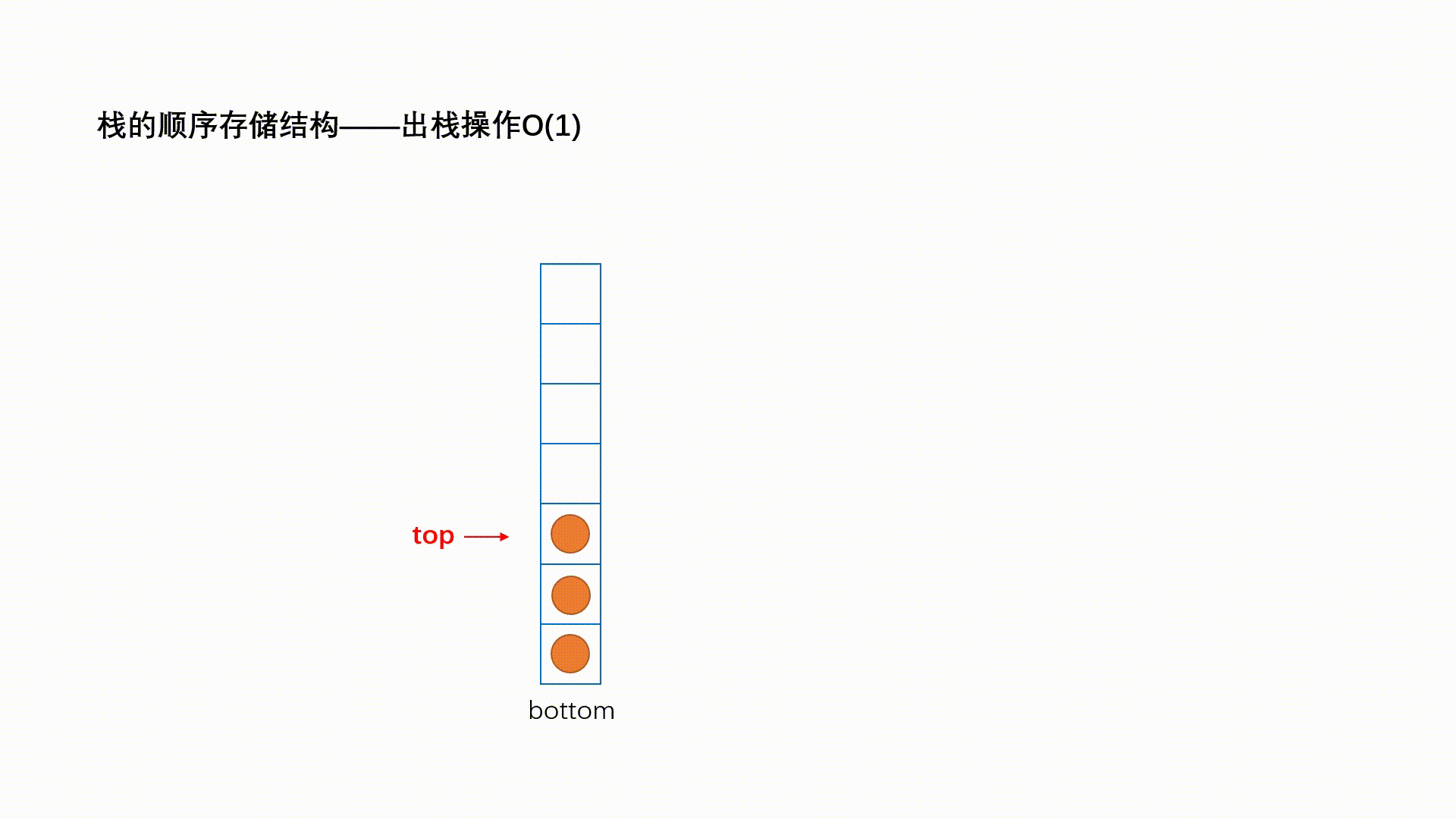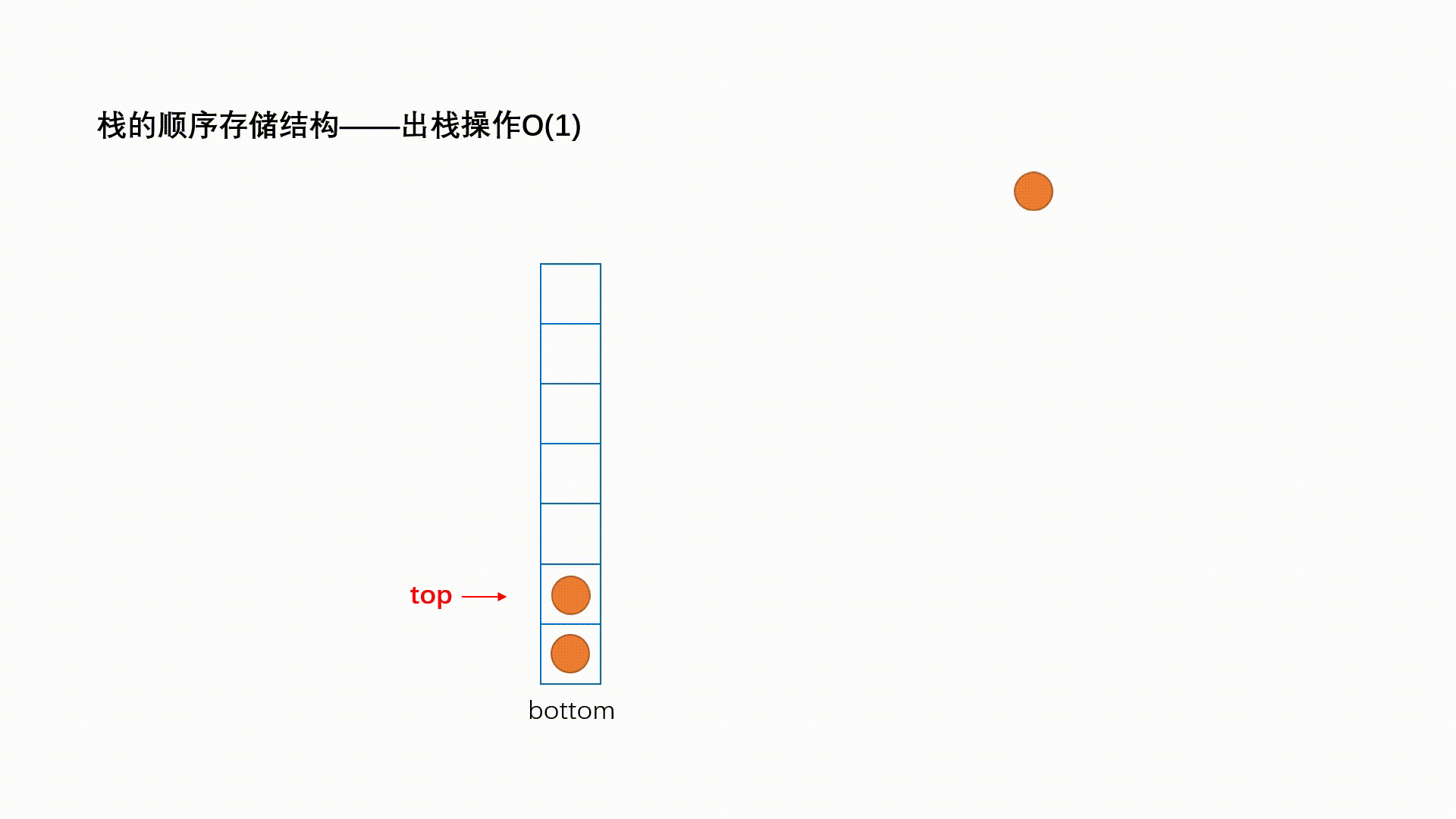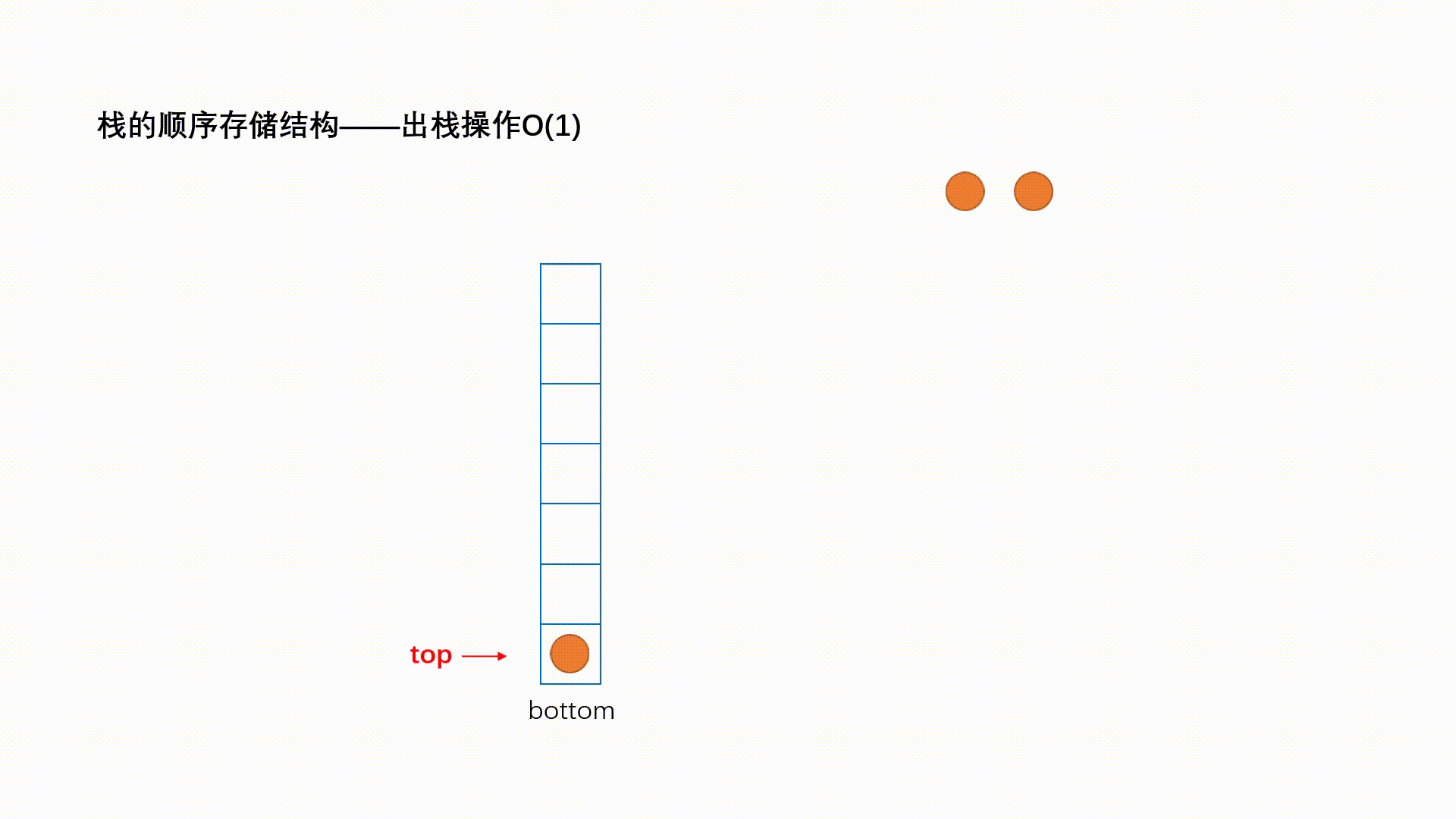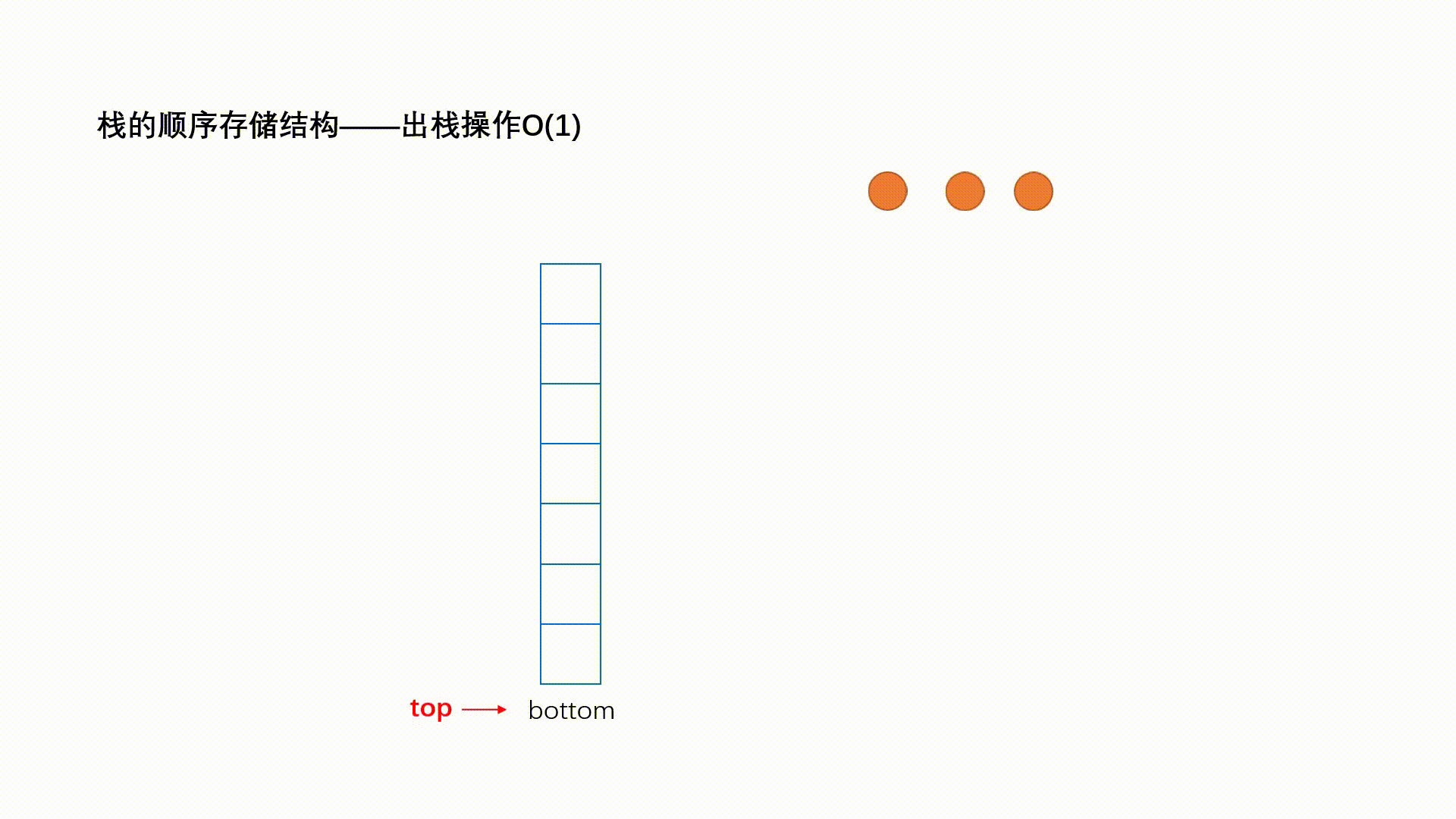
Ⅱ、出栈

出栈：栈的删除操作叫做出栈。出数据在栈顶。

int pop(Stack *s) { 
    if(empty(s)) return 0; //（1） s->top = s->top -1; //（2） return 1; } 

（1）如果栈为空，直接结束

（2）出栈 ：将栈顶 减一 即可

四、队列的概念

1、定义

只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 。

想象一下排队买票的场景。每个人都会排在队伍的尾部，而排在队伍最前面的人会最先买到票并离开队伍。这个过程类似于队列的入队和出队操作。最先进入队伍的人会最先离开队伍，而最后进入队伍的人则会最后离开队伍。

2、操作

通常对队列执行以下两种操作：
向队列中添加元素，此过程被称为”入队”；
从队列中提取出指定元素，此过程被称为”出队”；

五、队列的实现

1、顺序表实现

Ⅰ、队列的假溢出

队列是一种数据结构，可以将其看作是一个排队等待的队伍。在队列中，元素的添加（入队）和移除（出队）遵循先进先出（FIFO）的原则，即最早进入队列的元素最先被移除。队列有一个队头和队尾，新元素从队尾添加，而元素从队头移除。

队列溢出指的是当队列已满，也就是说它已经包含了最大允许的元素数量，但我们仍试图向其中添加新元素时发生的现象。此时，由于队列无法容纳更多的元素，队列溢出就发生了。而队列的假溢出是指队列中，队列尾部的空闲空间实际上可以容纳新的元素，但由于队列的逻辑结构限制（队列头和尾是相邻的），导致空间不能被利用，从而产生的一种溢出现象。实际上，这种溢出并非真正意义上的溢出，因为队列仍然具有可用空间。这就是为什么称为“假溢出”。

如下图所示，数组的前两个位置明明就是空的，但是却由于数组的最后一个位置有数据导致新数据无法正常加入。

为了解决假溢出的问题，可以使用循环队列的概念。循环队列是一种特殊类型的队列，其中队尾可以连接到队头，从而实现有效地使用队列空间。在循环队列中，当队尾指针到达数组的末尾时，它将循环回到数组的起始位置，继续使用队列中的空闲空间。这样就避免了假溢出的情况。

Ⅱ、队列的定义

为了用顺序表实现队列，我们还要定义一下顺序表。

typedef struct vector { 
    int *data; //数据区 int size; //数据大小 } vector; 

使用顺序表定义队列

typedef struct Queue { 
    vector *data; //数据存储区域 int size, head, tail, count; //总大小、队列头指针、队列尾指针、循环 } Queue; 

Ⅲ、初始化队列

//初始化有一个大小为n的顺序表 vector *initVector(int n) { 
    vector *v = (vector *)malloc(sizeof(vector)); v->size = n; //初始化一个顺序表的数据区域 v->data = (int *)malloc(sizeof(int) * n); return v; } 

Queue *initQueue(int n) { 
    //申请出一个队列空间 Queue *q = (Queue *)malloc(sizeof(Queue)); //初始化数据区域 q->data = initVector(n); //初始化顺序表大小 q->size = n; //初始化头尾指针，循环队列 q->head = q->tail = q->count = 0; return q; } 

Ⅳ、销毁队列

void clearVector(vector *v) { 
    if (v == NULL) return ; free(v->data); free(v); return ; } 

void clearQueue(Queue *q) { 
    if (q == NULL) return ; //清理数据区域 clearVector(q->data); //释放队列本身的空间 free(q); return ; } 

Ⅴ、队列判空

//队列判空 int empty(Queue *q) { 
    return q->count == 0; } 

Ⅵ、查看队首元素

//查看顺序表中的某一个值 int vectorSeek(vector *v, int pos) { 
    if (pos < 0 || pos >= v->size) return -1; return v->data[pos]; } 

int front(Queue *q) { 
    //直接返回指向的那个元素值 return vectorSeek(q->data, q->head); } 

Ⅶ、入队出队

入队操作的返回值代表入队成功。

什么时候入队不成功？当队列满了的时候就不成功。

//入队操作 int push(Queue *q, int val) { 
    if (q->count == q->size) return 0; //队列满了，入队失败 insertVector(q->data, q->tail, val);//调用顺序表的插入操作 q->tail += 1; //完成数据插入，调整tail指针位置 if (q->tail == q->size) q->tail = 0; //调整位置，形成循环利用，防止假溢出 q->count += 1; //count + 1 return 1; //入队成功 } 

//出队操作 int pop(Queue *q) { 
    if (empty(q)) return 0; //队列为空，直接返回0，出队失败 q->head += 1; //头指针向后移动一位  // 注意这里有个小 bug，由于是循环队列，别忘了判断 head 是否越界 if (q->head == q->size) q->head = 0; q->count -= 1; return 1; } 

2、单链表实现

在顺序表实现的队列中，队列的大小是预先固定的，当队列满时，即使实际上有空闲的空间，也无法将新元素插入队列。这种现象被称为“假溢出”。为了解决这个问题，我们通常需要实现一个循环队列，这样可以在队列满时使用空闲空间。

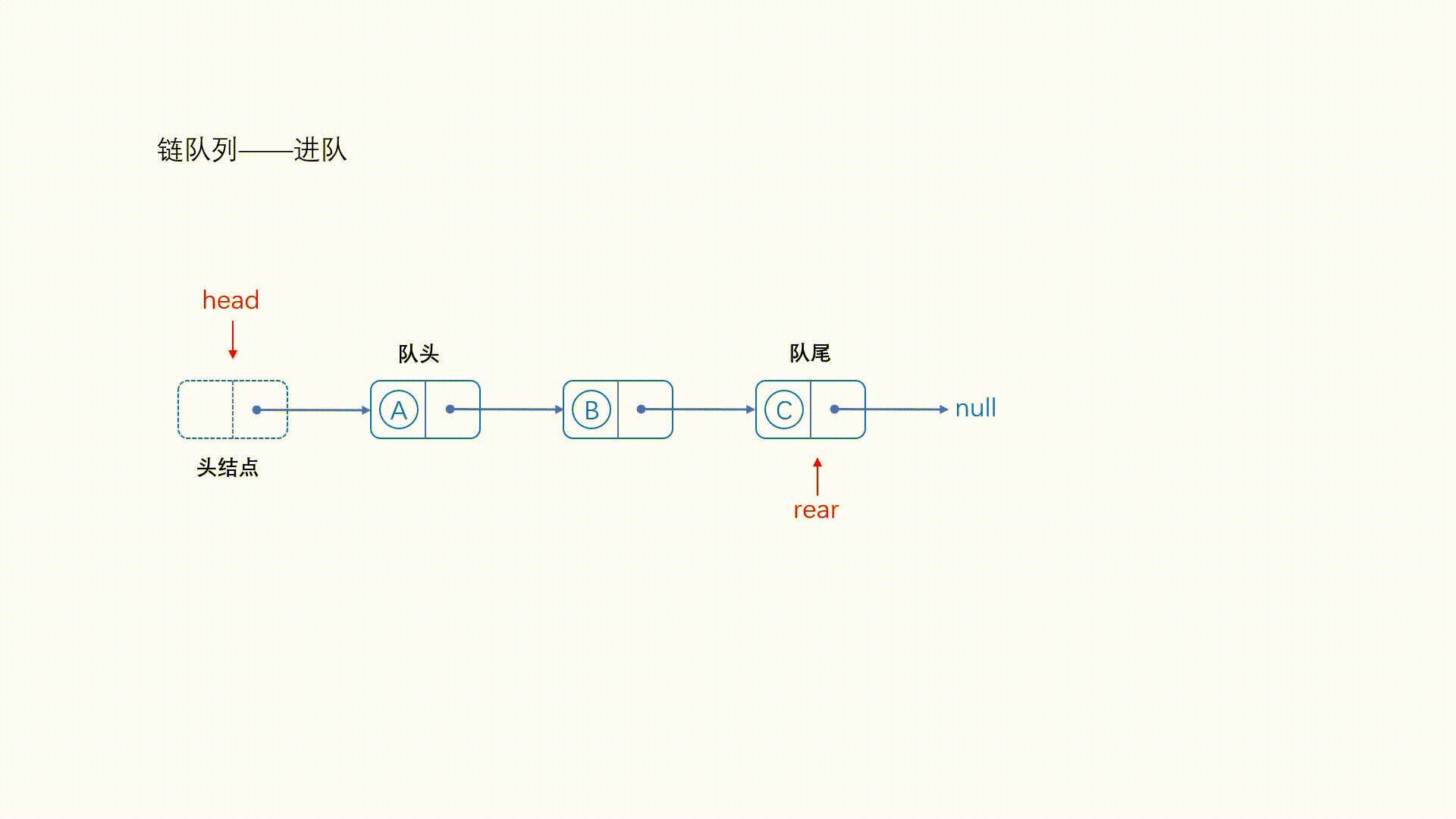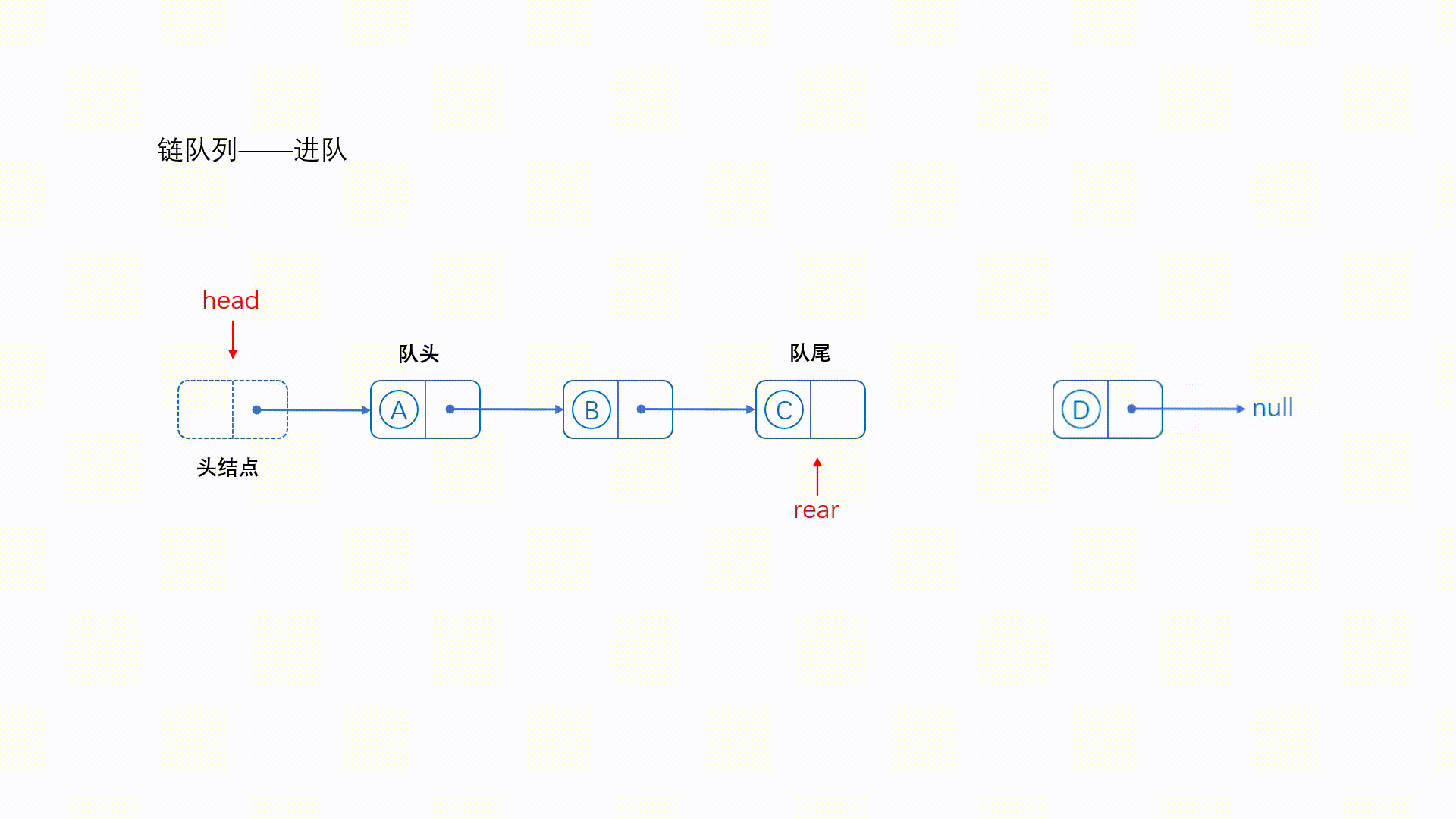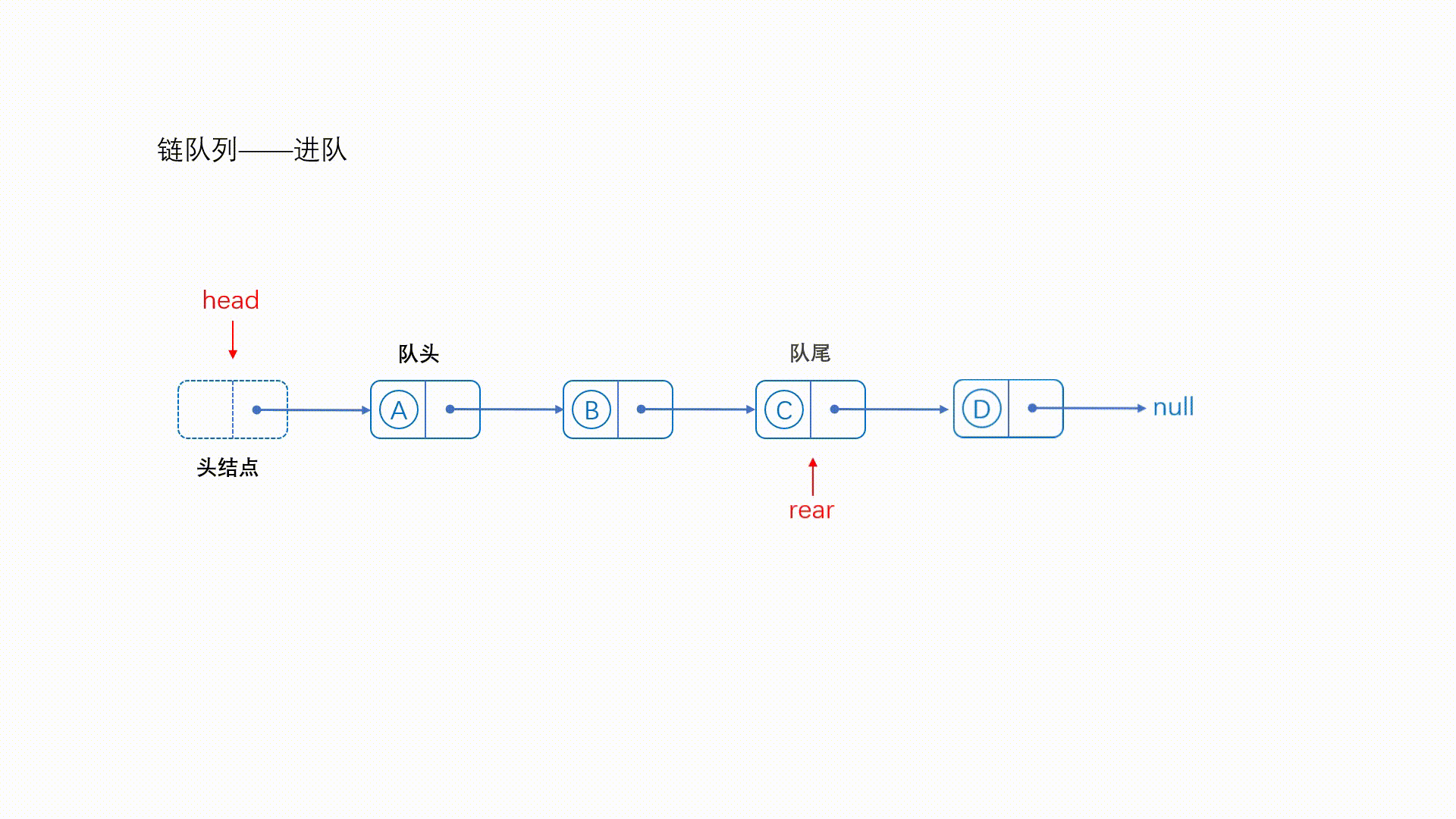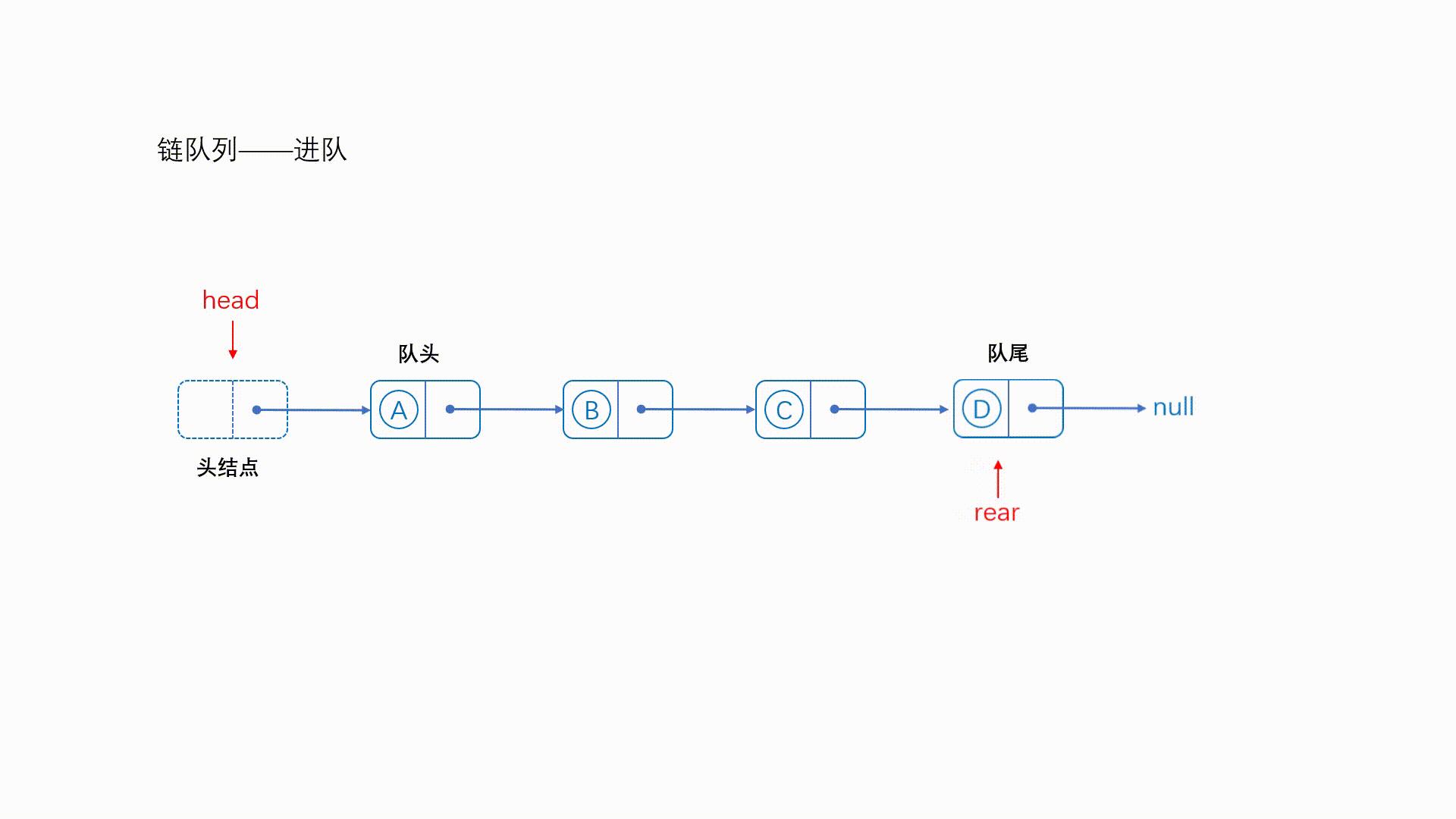
然而，在链表实现的队列中，我们并不需要预先分配固定大小的内存。当需要插入新元素时，我们可以动态地为新节点分配内存，并将其添加到链表中。同样，当删除元素时，我们可以释放相应节点的内存。因此，链表实现的队列不会遇到假溢出现象，因为只要系统内存允许，我们可以继续分配空间来扩展队列。

Ⅰ、队列的定义

//链表的节点结构 typedef struct Node { 
    int data; Node *next; } Node; //实现一个有头链表 typedef struct LinkList { 
    Node head, *tail; } LinkList; 

typedef struct Queue { 
    LinkList *l; //因为底层结构变成了链表，所以不在乎存储空间大小，不用考虑假溢出 int count; } Queue; 

Ⅱ、初始化队列

//初始化链表 LinkList *initLinkList() { 
    LinkList *l = (LinkList *)malloc(sizeof(LinkList)); l->head.next = NULL; // 头节点的下一个节点指针初始化为 NULL l->tail = &(l->head); // 尾节点指针指向头节点 return l; } 

Queue *initQueue() { 
    Queue *q = (Queue *)malloc(sizeof(Queue)); q->l = initLinkList(); //初始化队列中的链表 q->count = 0; return q; } 

Ⅲ、销毁队列

//销毁链表 void clearLinkList(LinkList *l) { 
    Node *p = l->head.next, *q; while (p) { 
    q = p->next; free(p); p = q; } free(l); return ; } 

//销毁队列 void clearQueue(Queue *q) { 
    if (q == NULL) return ; clearLinkList(q->l); //销毁队列中的链表 free(q); //销毁队列本身 return ; } 

Ⅳ、队列判空

int empty(Queue *q) { 
    return q->count == 0; } 

Ⅴ、查看队首元素

//链表判空 int emptyList(LinkList *l) { 
    return l->head.next == NULL; } //查看链表首元素 int frontList(LinkList *l) { 
    if (emptyList(l)) return 0; return l->head.next->data; } 

int front(Queue *q) { 
    if (empty(q)) return 0; return frontList(q->l); //返回链表存储的第一个数据 } 

Ⅵ、 入队出队

入队操作：

• 使用 getNewNode 函数创建一个新节点，将入队元素存储在新节点的 data 成员中。
• 更新链表尾节点指针 tail 的 next 成员，使其指向新节点。
• 更新尾节点指针 tail，使其指向新节点。
• 增加队列元素计数。

  

//创建一个新的链表节点 Node *getNewNode(int val) { 
    Node *p = (Node *)malloc(sizeof(Node)); p->data = val; p->next = NULL; return p; } //在链表的最后位置加入一个新链表 int insertTail(LinkList *l, int val) { 
    Node *node = getNewNode(val); l->tail->next = node; l->tail = node; return 1; } //队列的入队 int push(Queue *q, int val) { 
    insertTail(q->l, val); //在链表的末尾增加一个值 q->count += 1; // 更新队列元素个数 return 1; } 

出队操作：

• 检查链表是否为空。如果为空，说明队列中没有元素可以出队。
• 保存链表头节点的下一个节点指针（即队头元素的节点）。
• 更新链表头节点的 next 成员，使其指向队头元素的下一个节点。
• 如果队头元素是尾节点，更新尾节点指针 tail，使其指向头节点。
• 释放队头元素的节点内存。
• 减少队列元素计数。

  

  //链表判空 int emptyList(LinkList *l) { 
        return l->head.next == NULL; } //删除链表的头元素 int eraseHead(LinkList *l) { 
        if (emptyList(l)) return 0; // 如果链表为空，返回 0，表示没有元素可删除 Node *p = l->head.next; // 保存头部节点（即队头元素所在的节点） l->head.next = l->head.next->next; // 更新头节点的下一个节点指针，使其指向队头元素的下一个节点 if (p == l->tail) l->tail = &(l->head); // 如果删除的是尾节点，更新尾节点指针为指向头节点 free(p); // 释放头部节点（队头元素所在的节点）的内存 return 1; } //出队操作 int pop(Queue *q) { 
        eraseHead(q->l); //删除链表中的第一个元素 q->count -= 1; return 1; } 

  

  3、两者区别

  Ⅰ、顺序表实现的队列

  顺序表（基于数组）实现队列时，通常采用循环队列的策略。队列的头部和尾部都会随着入队和出队操作移动，当达到数组边界时会回到数组起始位置。为了避免队列满和队列空的判断条件冲突，通常会预留一个空间不用于存储元素。

​ 优点：

• 访问速度快：数组具有较好的随机访问性能，可以通过下标直接访问元素。
• 空间利用率高：顺序表的存储空间是连续的，没有额外的指针开销。

  缺点：

• 产生假溢出：当队列未满但数组已经无法容纳新元素时，需要进行循环队列调整，否则会产生假溢出。
• 大小固定：顺序表的大小在创建时就已经确定，不能动态调整。如果空间过大，会造成空间浪费；如果空间过小，可能导致溢出。
  

  Ⅱ、单链表实现的队列

  单链表实现队列： 单链表实现队列时，头部节点用于出队，尾部节点用于入队。每次入队时，在尾部添加新节点；每次出队时，删除头部节点并释放其内存。

优点：

• 动态分配空间：单链表实现的队列可以在运行时动态分配和释放内存，避免了假溢出现象。
• 实现简单：单链表实现队列时，只需在头部和尾部进行操作，不需要循环队列策略，实现相对简单。

缺点：

• 空间开销较大：单链表需要额外的指针存储节点之间的关系，导致额外的空间开销。
• 访问速度相对较慢：链表无法像数组那样直接通过下标访问元素，需要遍历链表节点。