概率论简介

大家好，欢迎来到IT知识分享网。

概率论（英语：Probability theory）是集中研究概率及随机现象的数学分支，是研究随机性或不确定性等现象的数学。

• 概率论主要研究对象为随机事件、随机变量以及随机过程。对于随机事件是不可能准确预测其结果的[1]，然而对于一系列的独立随机事件——例如掷骰子、扔硬币、抽扑克牌以及轮盘等，会呈现出一定的、可以被用于研究及预测的规律[2]，两个用来描述这些规律的最具代表性的数学结论分别是大数定律和中心极限定理。

例子

• 转盘游戏：
  • 在游戏中玩家可能认为，在连续出现多次红色后，出现黑色的概率会越来越大。这种判断也是错误的，即出现黑色的概率每次是相等的，因为球本身并没有“记忆”， 它不会意识到以前都发生了什么，其概率始终是0.5但轮盘的前后期开奖数字形成时间序列（可能存在自回归模型）。
    
• 生日悖论：
  • 在一个足球场上有23个人（2×11个运动员和1个裁判员），
    不可思议的是，在这23人当中至少有两个人的生日是在同一天的概率要大于50％。 如果这23人都没有相同的生日也不违反概率，只是小于50％。

历史

• 作为数学统计基础的概率论的创始人分别是法国数学家帕斯卡和费马，其可追溯到公元17世纪。当时的法国宫廷贵族里盛行着掷骰子游戏，游戏规则是玩家连续掷4次骰子，如果其中没有6点出现，玩家赢，如果出现一次6点，则庄家（相当于现在的赌场）赢。按照这一游戏规则，从长期来看，庄家扮演赢家的角色，而玩家大部分时间是输家，因为庄家总是要靠此维生的，而当时人们也接受了这种现象。
• 后来为了使游戏更刺激，游戏规则发生了些许变化，玩家这回用2个骰子连续掷24次，不同时出现2个6点，玩家赢，否则庄家赢。当时人们普遍认为，2次出现6点的概率是一次出现6点的概率的1 / 6，因此6倍于前一种规则的次数，也既是24次赢或输的概率与以前是相等的。然而事实却并非如此，从长期来看，这回庄家处于输家的状态，于是他们去请教当时的数学家帕斯卡，求助其对这种现象作出解释。
• 帕斯卡
  • 布莱士·帕斯卡（Blaise Pascal ）公元1623年6月19日出生于多姆山省奥弗涅地区的克莱蒙费朗，法国数学家、物理学家、哲学家、散文家。
    
• 费马
  • 皮埃尔·德·费马，法国律师和业余数学家。他在数学上的成就不比职业数学家差，他似乎对数论最有兴趣，亦对现代微积分的建立有所贡献。被誉为“业余数学家之王”，17世纪，法国的帕斯卡和费马研究了意大利的帕乔里的著作《摘要》，建立了通信联系，从而建立了概率学的基础。
    
  • 其他对概率论的发展作出重要贡献的人还有荷兰物理、数学家惠更斯，瑞士物理、数学家伯努利，法国数学家棣莫弗，法国数学、天文学家拉普拉斯，德国数学家高斯，法国物理、数学家泊松，意大利数学、医学家卡尔达诺以及苏联数学家柯尔莫哥洛夫。

定义

传统概率

• 传统概率又称为拉普拉斯概率，因为其定义是由法国数学家拉普拉斯提出的。如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验。

公理化定义：

• 设随机实验E的样本空间为Ω。若按照某种方法，对E的每一事件A赋于一个实数P(A)，且满足以下公理：
  （1）非负性：P(A)≥0；
  （2）规范性：P(Ω)=1；
  （3）可列（完全）可加性：对于两两互不相容的可列无穷多个事件A1，A2，……，An，……，有
  
  ，则称实数P(A)为事件A的概率。

事件

• 包括单位事件、事件空间、随机事件等。

  • 在一次随机试验中可能发生的唯一的，且相互之间独立的结果被称为单位事件，用e表示。
  • 在随机试验中可能发生的所有单位事件的集合称为事件空间，用S来表示。
  • 随机事件是事件空间S的子集，它由事件空间S中的单位元素构成，用大写字母A，B，C…表示。

事件的计算

• 因为事件在一定程度上是以集合的含义定义的，因此可以把集合计算方法直接应用于事件的计算，也就是说，在计算过程中，可以把事件当作集合来对待。
  • A的补集：不属于A的事件发生
    
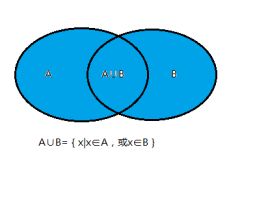
  • 并集A∪B：或者A或者B或者A，B同时发生
    
  • 交集A∩B：事件A，B同时发生
    
  • 差集A\B：不属于B的A事件发生）
    
  • 空集A∩B=∅：A，B事件不同时发生
  • 子集B⊆A：如A发生，则B也一定发生
    

条件概率

• 一事件A在一事件B确定发生后会发生的概率称为B给之A的条件概率；其数值为 （当 时）。若B给之A的条件概率和A的概率相同时，则称A和B为独立事件。

定理

定理1

• 又称互补法则。与A互补事件的概率始终是1-P(A)。
  第一次旋转红色不出现的概率是19/37，按照乘法法则，第二次也不出现红色的概率是
  
  ，因此在这里互补概率就是指在两次连续旋转中至少有一次是红色的概率，为

定理2

• 不可能事件的概率为零。
  证明： Q和S是互补事件，按照公理2有P(S)=1，再根据上面的定理1得到P(Q)=0

定理3

• 如果A1…An事件不能同时发生（为互斥事件），而且若干事件A1，A2，…An∈S每两两之间是空集关系，那么这些所有事件集合的概率等于单个事件的概率的和。
  例如，在一次掷骰子中，得到5点或者6点的概率是：
  

定理4

• 如果事件A，B是差集关系，则有
  

定理5

• 任意事件加法法则：
  对于事件空间S中的任意两个事件A和B，有如下定理： 概率
  

定理6

• 乘法法则：
  事件A，B同时发生的概率是：
  
  ，前提为事件A,B有一定关联。

定理7

• 无关事件乘法法则：
  两个不相关联的事件A，B同时发生的概率是：注意到这个定理实际上是定理6(乘法法则)的特殊情况，如果事件A，B没有联系，则有P(A|B)=P(A)，以及P(B|A)=P(B)。观察一下轮盘游戏中两次连续的旋转过程，P(A)代表第一次出现红色的概率，P(B)代表第二次出现红色的概率，可以看出，A与B没有关联，利用上面提到的公式，连续两次出现红色的概率为：
  
  忽视这一定理是造成许多玩家失败的根源，普遍认为，经过连续出现若干次红色后，黑色出现的概率会越来越大，事实上两种颜色每次出现的概率是相等的，之前出现的红色与之后出现的黑色之间没有任何联系，因为球本身并没有”记忆”，它并不”知道”以前都发生了什么。
  所以，连续10次至少有1次出现红色的概率为
  

统计概率编辑

• 统计概率是建立在频率理论基础上的，分别由英国逻辑学家约翰(John Venn,1834-1923)和奥地利数学家理查德(Richard VonMises,1883-1953)提出，他们认为，获得一个事件的概率值的唯一方法是通过对该事件进行100次，1000次或者甚至10000次的前后相互独立的n次随机试验，针对每次试验均记录下绝对频率值和相对频率值hn(A)，随着试验次数n的增加，会出现如下事实，即相对频率值会趋于稳定，它在一个特定的值上下浮动，也即是说存在着一个极限值P(A)，相对频率值趋向于这个极限值。
  这个极限值被称为统计概率，表示为：