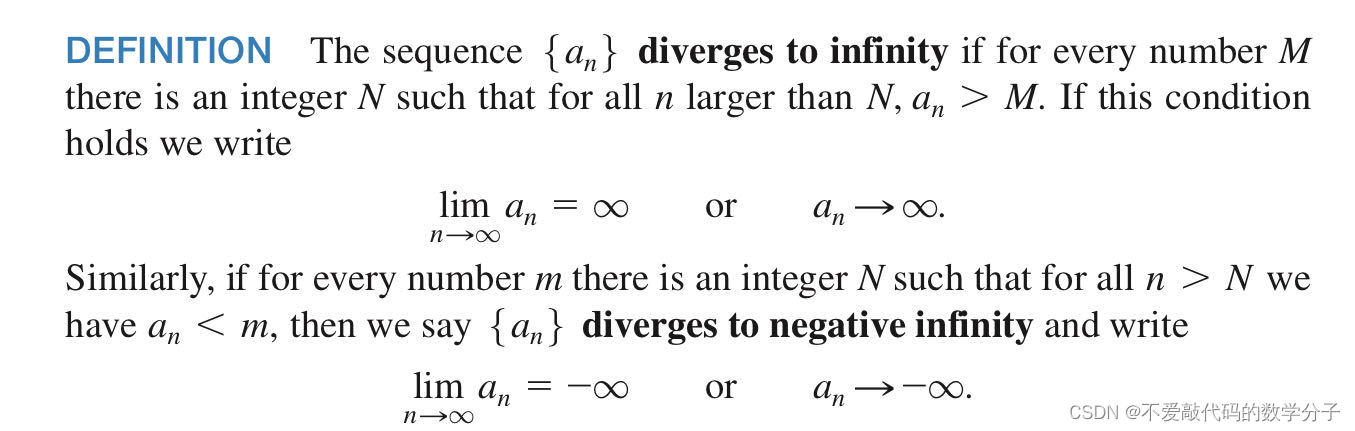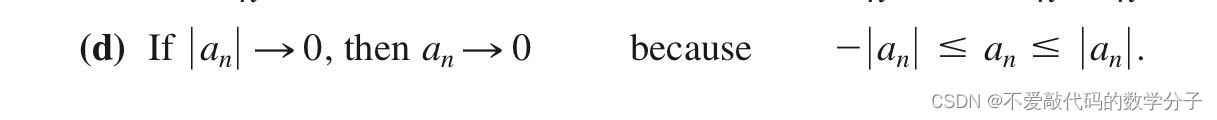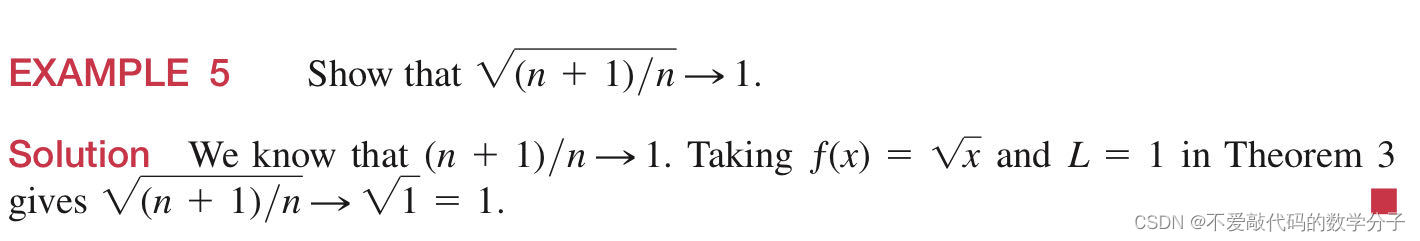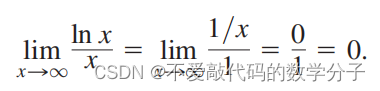大家好，欢迎来到IT知识分享网。
目录
数列
定义
一个数列就是一列数字（定义非常简单，数列就是一些数字按照一定的顺序排列得到的）
a1 , a2 , a3 , . . . , an , . . .
例如：2, 4, 6, 8, 10, 12, . . . , 2n, . . .
数列an本身具有通项公式和递推公式两种性质（可以根据数列的递推公式得到通项公式），通项公式可以很好的反应这一组数列的性质，例如可以根据通项公式判断数列是递增的或者是递减的或者是常数列，还可以判断一些特殊数列是等差数列或者是等比数列。
收敛与发散
如果有一组数列递增，那么这组数列是一直增长没有边界还是增长到某一程度后趋近于特定的值；如果数列递减，那么这组数列是一直减小没有边界还是减小到某一程度后趋近于特定的值。
例如：
明显地，这组数列随着n的增大，值越来越趋近于0，那么我们称这组数列是收敛的（convergent）。
例如：
明显地，这组数列随着n的增大，值也越来越大且没有边界，那么我们称这组数列是发散的（divergent）。
上面只是给大家举了两个浅显的例子，下面我们根据严格的定义了解敛散性。
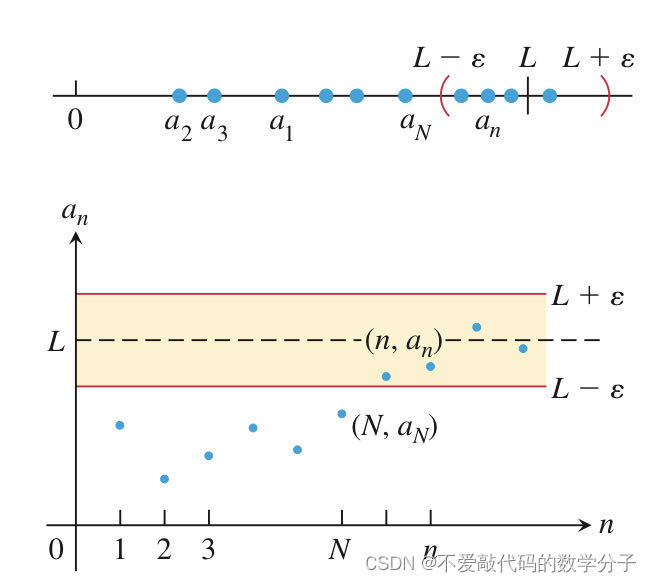
根据定义和图像，数列｛an｝是一组摆动数列。如果对于任意正数
都存在一个对应的N，那么当下标n大于N时（N可以看作一个界，当n>N时，后面的式子才会满足），an的值才会被限制在（L-，L+）。其中L是{an}的极限值。
如果没有一个像L的值存在，那么{an}是发散的。
判断数列敛散性与判断函数的敛散性方法是相似的，在后面提到的三明治定理同样可以适用于数列极限的判断
发散分为两种，一种是{an}发散到负无穷，另一种是{an}发散到正无穷
计算数列的极限
如果一组数列是收敛的，那么我们就比较关心这组数列是收敛到什么地方，也就是这组数列的极限是什么。因为数列是一种特殊的函数（数列在图像上以点的形式存在，并不连续，并且数列的下标，也就是定义域都为正数），所以适用于函数的一些计算极限的方法同样也适用于计算数列的极限
不过要注意的一点是对Sum Rule的应用
例如an = { 1 ，2 ，3 ，4，. . . }；bn = { -1 ，-2 ，-3 ，-4 ，. . . }。{an+bn} = { 0 ，0 ，0 ，. . .}。
明显地，{an + bn}收敛到0.
其次，数列{an}的标量乘法{can}（其中c是常数）不影响{an}原有的敛散性。
同样地，三明治定理（夹逼定理）也适用于数列极限的计算
特殊地，如果|an| cn并且cn0，则-cn an cn ，an0。
类似于绝对收敛（absolutely convergence）
定理3与收敛数列{an}和连续函数f有关 ，如果{an}是一组收敛到L的收敛数列，f是一个在L处的连续函数并且在所有的an都有定义（定义域包含an所有的值），那么f(an)f(L)。
例题5中将当作数列{an}的通项公式，f(x)=√x(定义域是(0,+))，根据定理3，数列{an}收敛到L=1，f(x)在L=1处有定义(满足了定理3所需要的前提条件)，所以f()f(1)，f(1)=1。
使用洛必达法则
和之间的关系形象化了，它能够使我们使用洛必达法则去计算一些数列的极限。
定理4中的an = f(n)可以理解为f(x)是将an在坐标轴上的点串联起来的函数(a1 = f(1)，a2 = f(2)，…)
如果{an}是收敛函数并且收敛到L，那么f(x)也收敛到L。
定理4解读到这里好像并没有与洛必达法则产生联系，但是我们要清楚的是，数列在坐标轴图像上是不连续的，所以，数列没有导数，无法对数列进行求导也就无法计算一些特殊的数列的极限，那么如果将数列等价于连续的函数，就可以使用洛必达法则求其极限了。
例题7中的数列
，根据之前对数列求极限的方法是无法得到结果的，但是在学习函数的时候，我们知道，
类型是可以使用洛必达法则求其极限的，那么我们就把该数列等价成对应的函数
等价成连续的函数后我们就可以使用洛必达法则得到该数列的极限了。
常用极限
公式(5)中如果将正数n换成连续的x，就是函数中的两个重要极限之一(公式(5)中的x是任意常数，不是自变量)
公式(6)推导
递归的定义
前面我们提到了数列{an}的两种性质：通项公式和递推公式。我们可以根据递推公式进一步得到通项公式，也可以根据递推公式观察数列的一些性质。
例如
an = an-1 + 1，这是一个明显地等差数列，但是不推出通项公式我们也可以直接地观察到数列的后一项比前一项增加了1。
斐波那契数列
在高中学习数列的时候，我们经常碰到过有关斐波那契数列的题目。根据斐波那契数列的定义，数列的某一项(从第三项开始，第一项和第二项均为1)是前两项的和。an+1 = an + an–1 (n“>2)
{an} = { 1 ，1 ，2 ，3 ，5 ，8 ，13 ，21 ，34 ，55 ，89 ，. . . }
斐波那契数列在自然界中有很多应用，例如兔子繁殖数列。一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。假设在理想自然条件下兔子具有过度繁殖倾向并且所有兔子都不死，那么一年以后可以繁殖多少对兔子？
在前两个月兔子没有繁殖能力，兔子只有一对，从第三个月开始，兔子开始繁殖变成两对兔子，以此类推，若干月之后的成兔对数(成兔对数 = 前月成兔对数 + 前月幼仔对数(不具有繁殖能力的兔子))是符合斐波那契数列的(有兴趣的小伙伴可以试着做一张excel表格验证一下，这里不再过多赘述)
有界单调数列
有界数列定义
如果存在一个数M使得数列{an}所有的值anM，那么数列{an}是有上界的。如果M是数列{an}的上界并且没有再比M小的数列{an}的上界，那么称M为数列{an}的最小上界。下界以及最小下届的定义与之类似。
尽管所有的收敛数列都是有界的，但是不是所有的有界函数都是收敛的，例如数列{an} = ，数列{an}是有界的，但是它并不收敛到某一个数。
单调数列定义
数列通常分为四种数列：1、单调递增数列；2、单调递减数列；3、常数列；4、摆动数列。
单调有界数列
在上面提到，不是所有的有界函数都是收敛的，那么什么样的条件能够使数列收敛呢
定理6—如果一组数列{an}是单调有界的，那么这组数列是收敛的。
需要注意的是，定理6并没有表示收敛数列都是单调的，例如数列{an} = 是一组收敛且有界的数列，但是它并不单调。
总结
数列这个知识点其实对大学生来说并不陌生，在高考中也是重要考点，但是高中的数列很少与函数结合起来。其实根据上面的学习，我们应该可以体会到函数与数列其实是密不可分的。无论是在求数列的极限或是数列的常用极限，都能看到函数的影子。
函数与数列
函数与数列的关系—归结原则(海涅定理)
对任意以x0为极限的数列都有
(具体可以参考【高等数学】函数极限以及与数列极限的关系 – 知乎 (zhihu.com)）
与定理3所表达内容类似
函数极限与数列极限
函数极限与数列极限有一点不同，通常我们所说的数列极限是当n时数列的值(可能收敛到某个值也可能发散)，但是函数极限有不同的情况，求函数极限可以求函数自变量趋近于某个点时函数的值为多少，这个时候就要考虑函数在该点有没有定义；如果有定义，函数在该点是否连续(数列并不需要考虑这一点)，左极限与右极限是否相等(端点处单独考虑)，只有满足了这些条件后，我们才能对函数自变量趋近于某一点函数的值做出判断。
(完)
(在本周二刚刚结束微积分级数的考试，我觉得写一点东西可能对微积分的理解会更加深入，不过我觉得这次编写逻辑并不是很清晰，只是按照课本的顺序做一些讲解和批注。希望对读者有所帮助，我也会继续优化我的语言与逻辑，使其从观感上更加通俗易懂，后续会按照课本的顺序继续对级数做出解读，如果可能的话我也想发布一些计算机编程的东西，谢谢)
(如有讲解错误或是不严谨的地方，请指出，不胜感激)
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/151420.html
