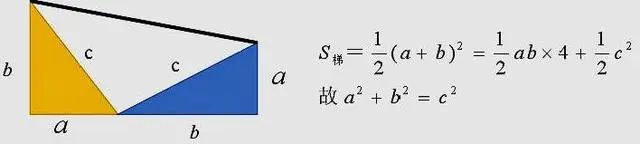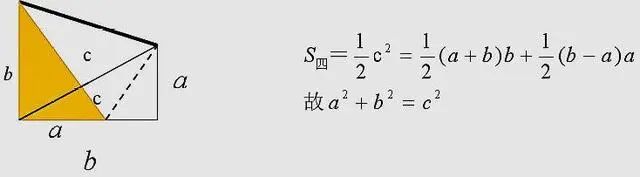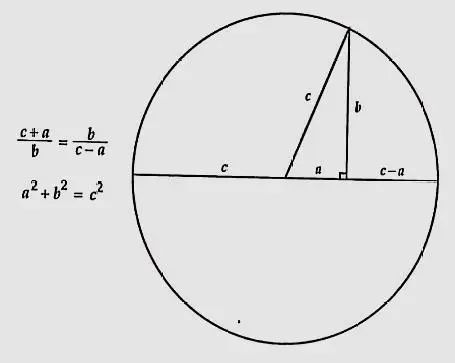大家好,欢迎来到IT知识分享网。
勾股定理是平面几何中最重要的定理!它是历史上第一个将数与形联系起来的定理,开启了论证几何的开端,甚至引发了第一次数学危机,勾股定理的发现使人们加深了对数的理解,发现了无理数。勾股定理也是历史上第一个给出完全解答的不定方程,并引出了费马大定理。而勾股定理的证明目前约有500种,是数学定理中证明方法最多的定理之一。今天我们来分享几种证明方法,从证明方法中感受勾股定理的魅力,加深对勾股定理的理解。反正我是只消化了几种,哈哈。
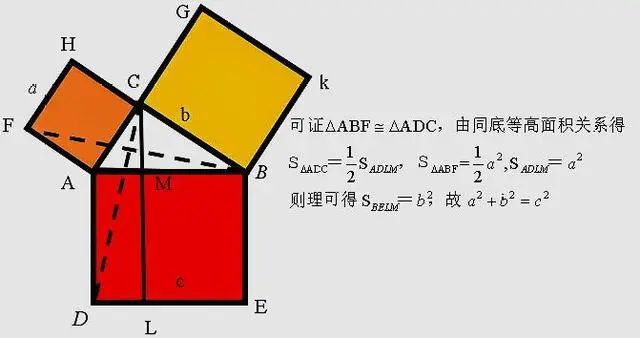
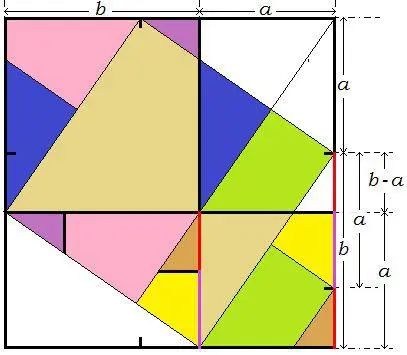
方法一:赵爽弦图证法
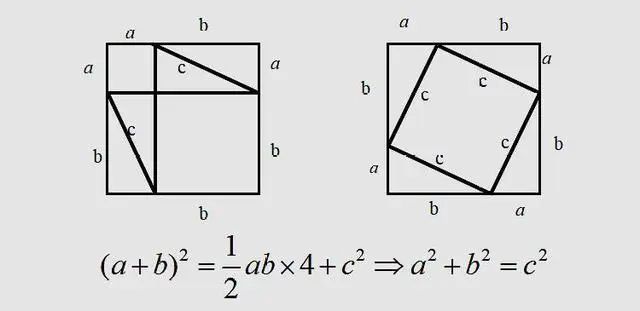
方法二:毕达哥拉斯证法
方法三:书本证明方法
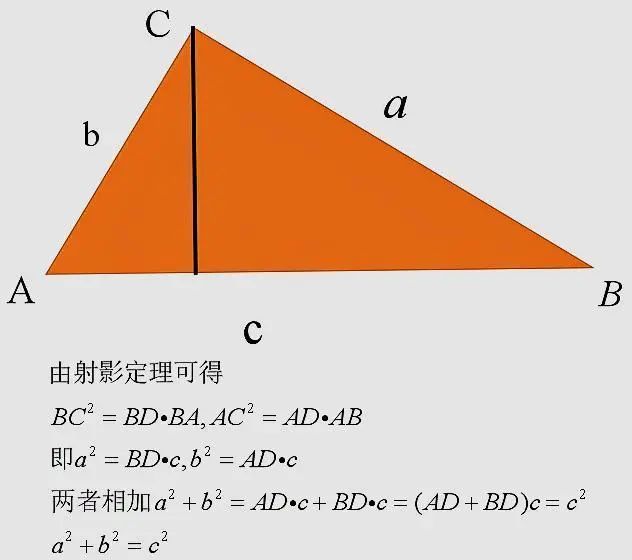
法四:利用三角形相似推导
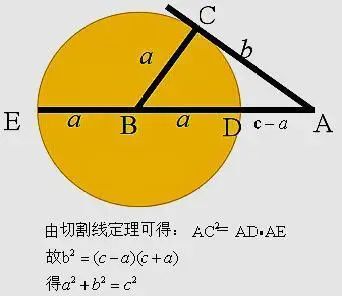
方法五:切割线定理证明
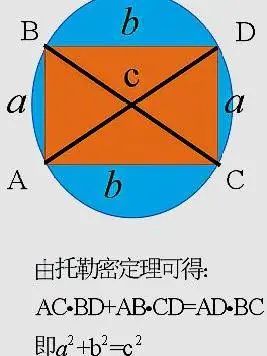
方法六:托勒密定理证明
方法七:利用切线长定理
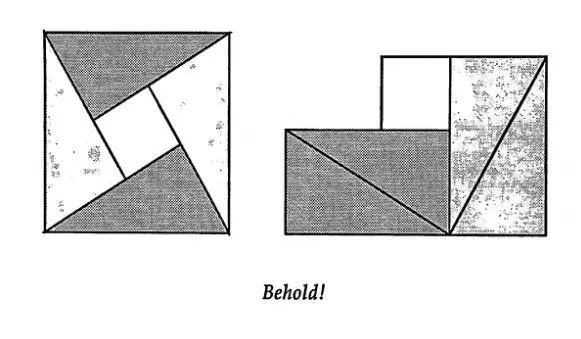
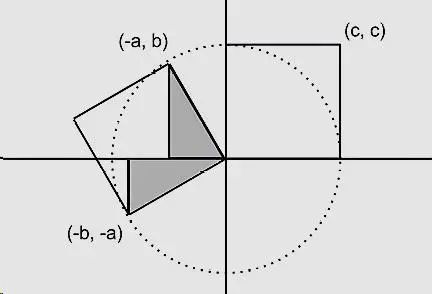
方法八:总统证法
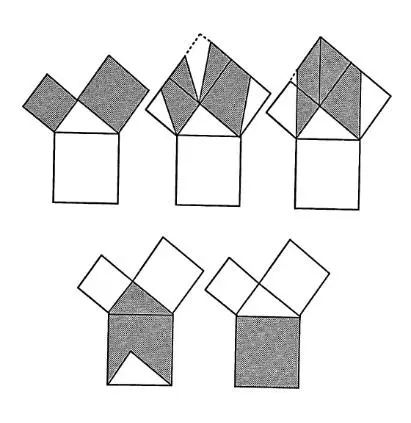
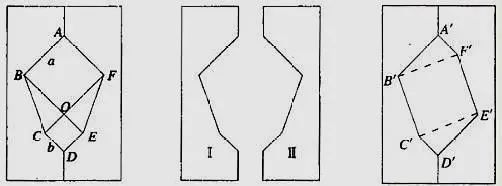
方法九:八法变式
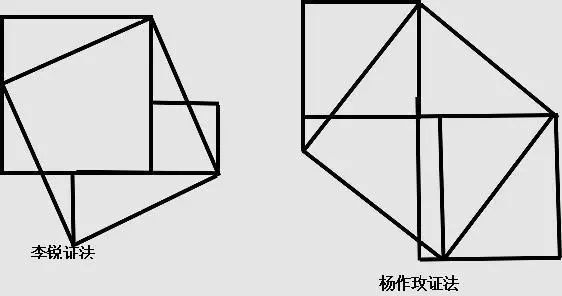
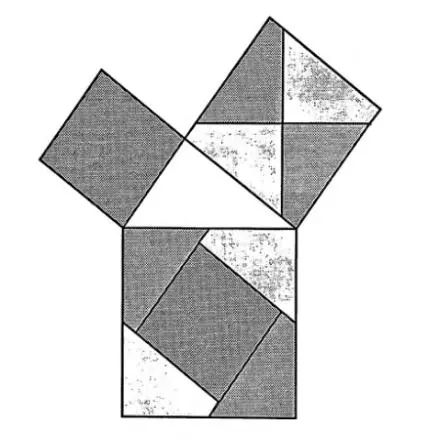
方法十和方法十一:
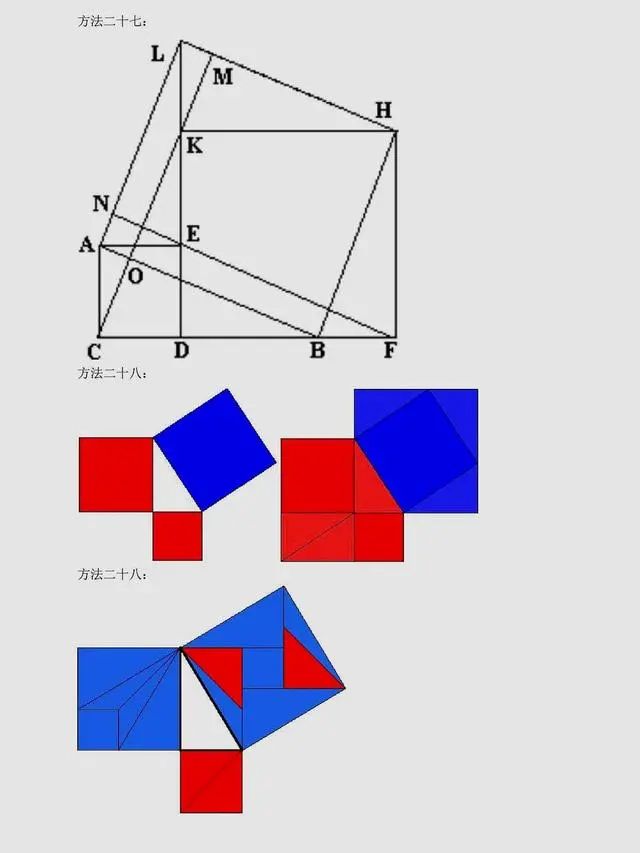
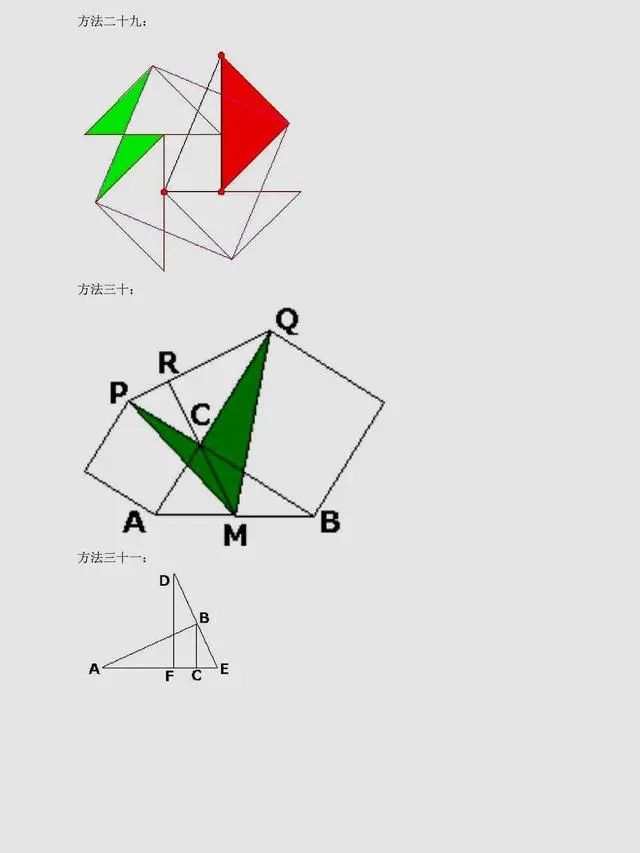
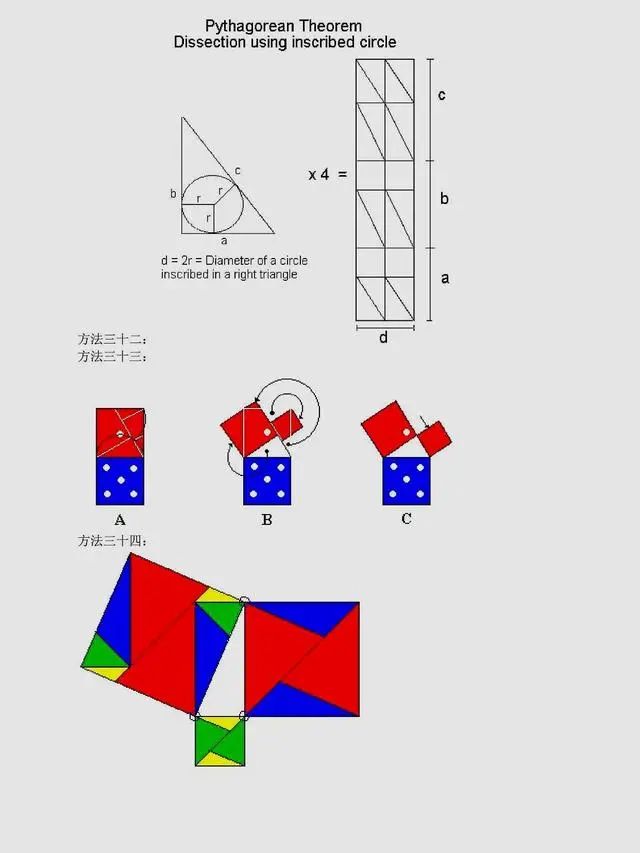
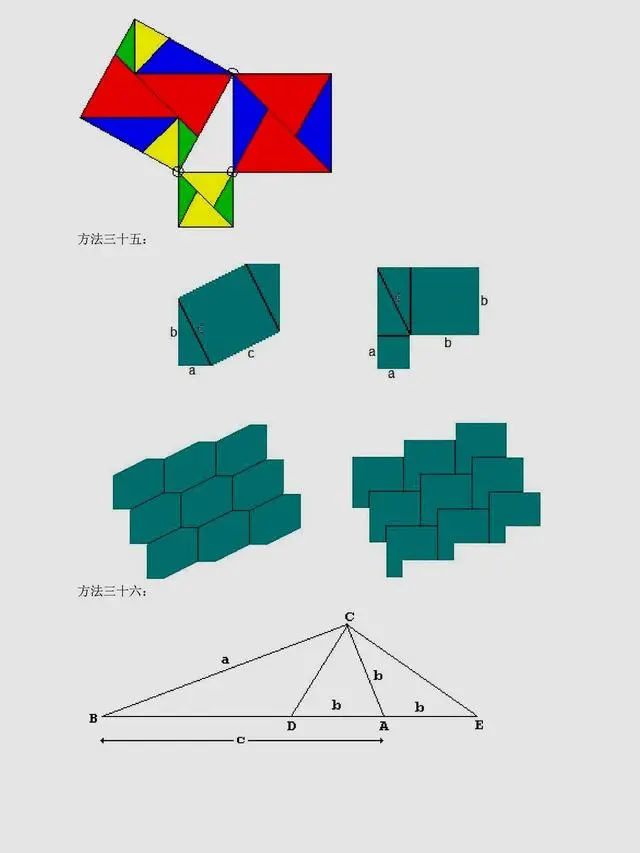
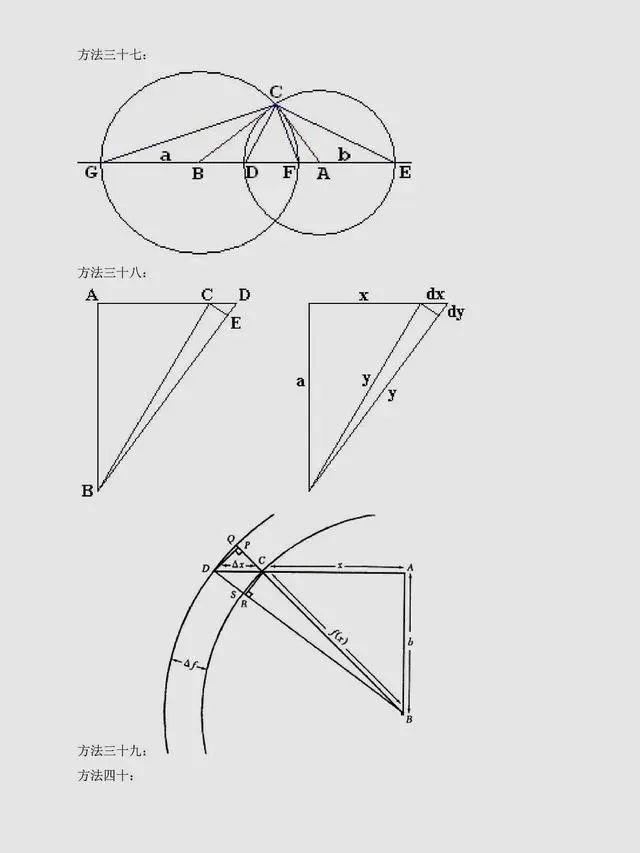
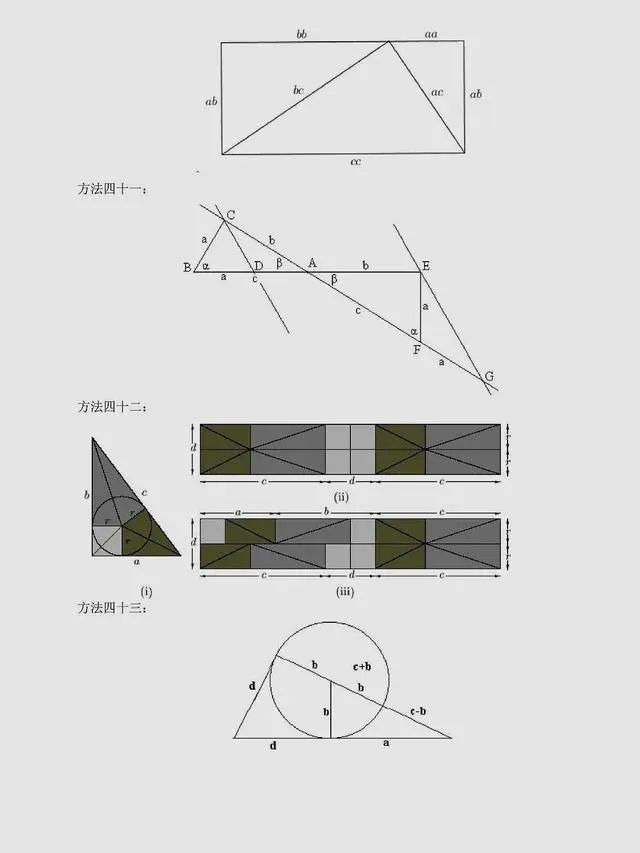
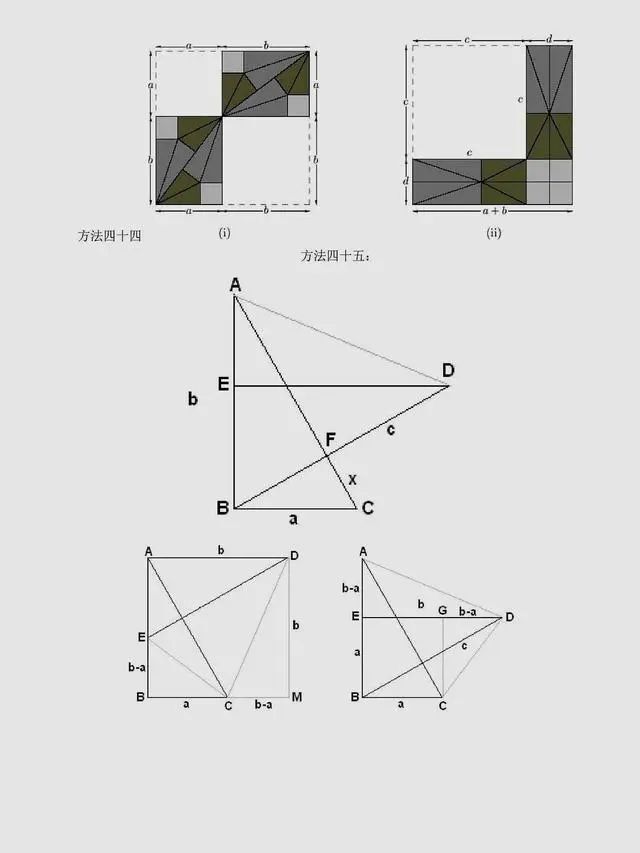
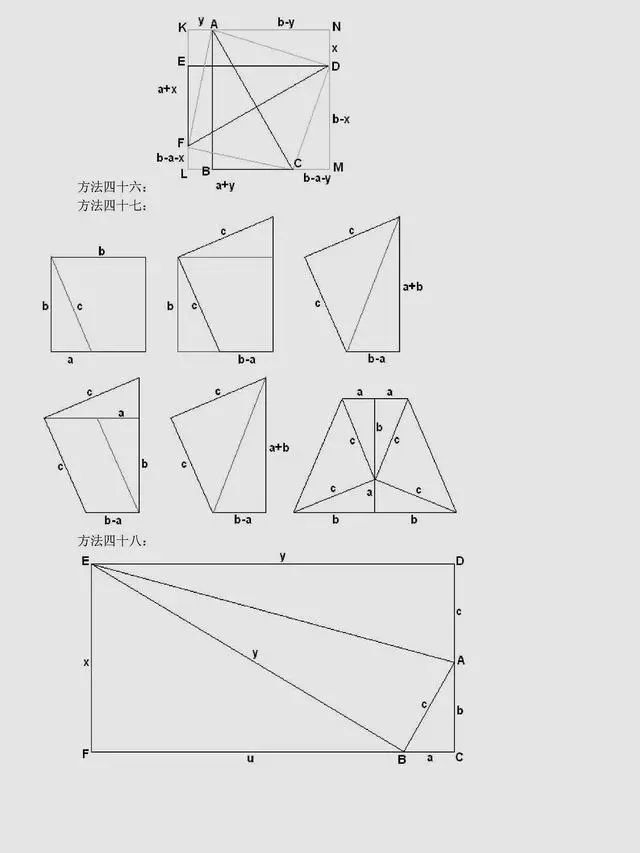
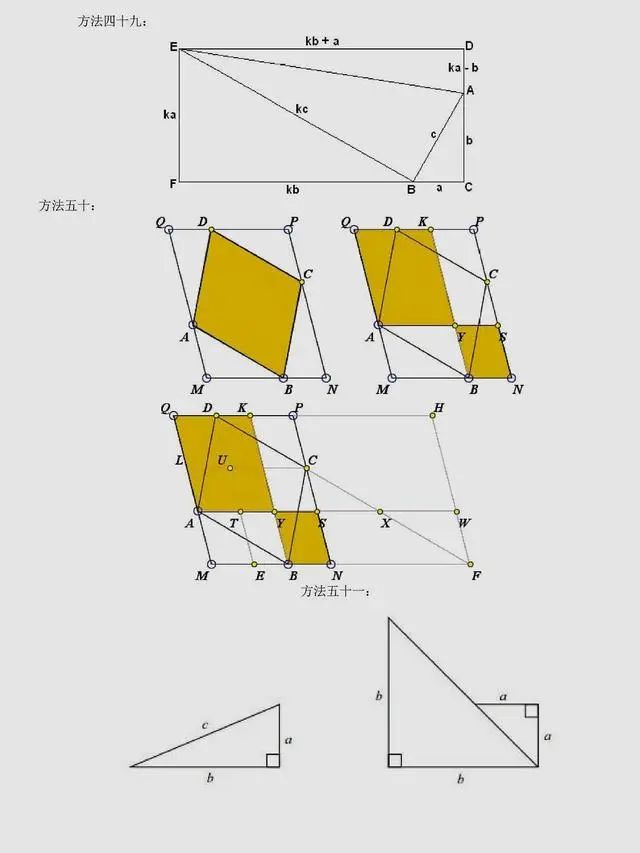
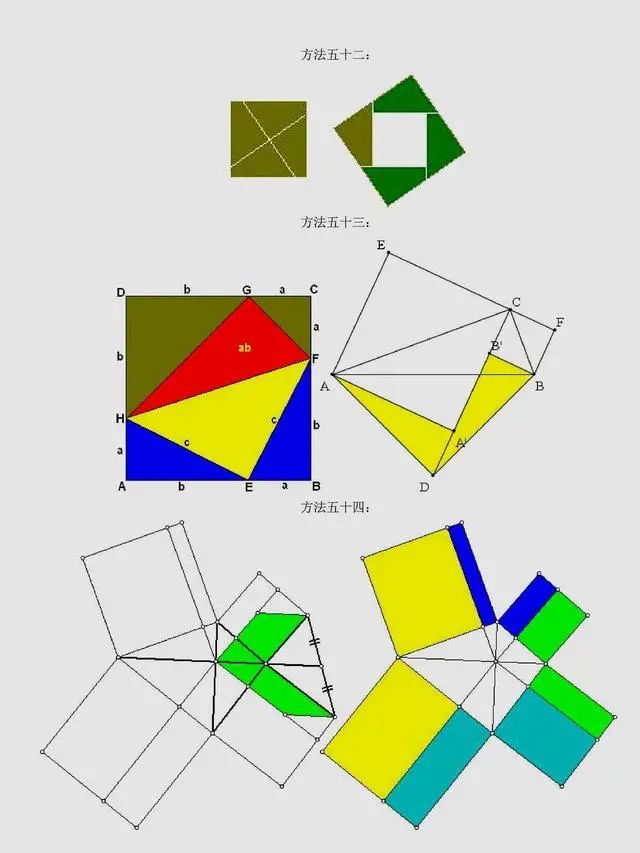
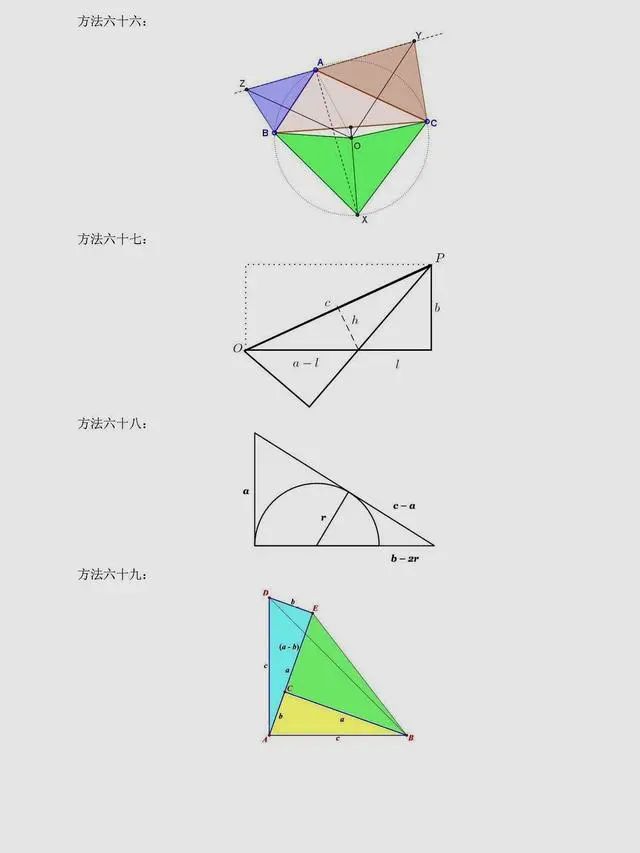
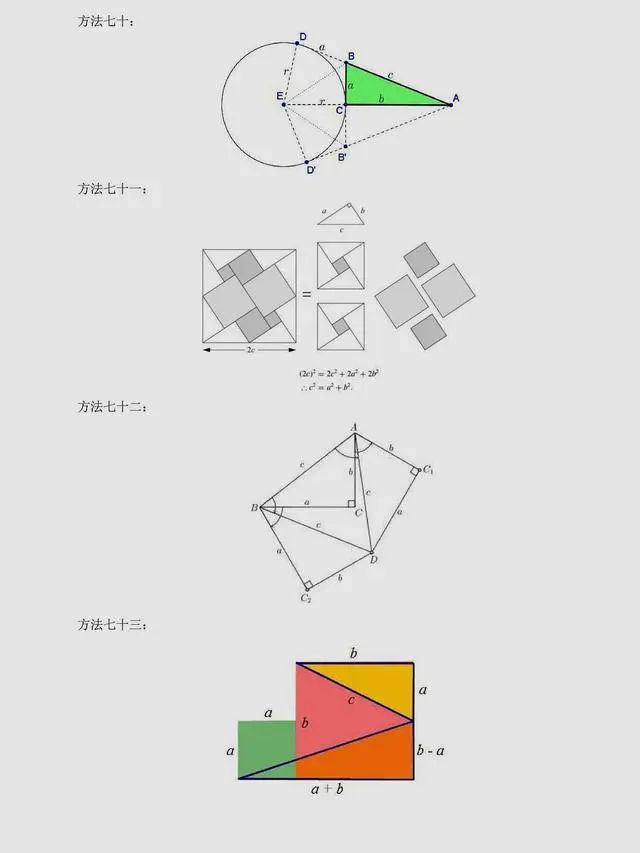
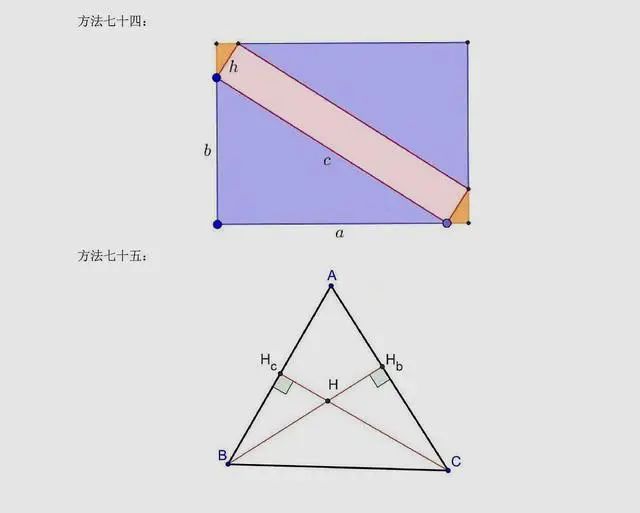
总结:上述方法是非常常见的方法,当然同学们可以总结出,用到最多的还是面积法,对于面积法无论证明方法如何变化,图形如何变化,方法都有一种熟悉感。同时,还有很多其它与圆相关的定理应用,要理解它们,同学们要掌握更多的相关知识。以下方法,只展示图片,同学们可以自行感悟。
方法十二:
方法十三:面积法
方法十四:拼接法1
方法十五:拼接法2
方法十六:射影定理
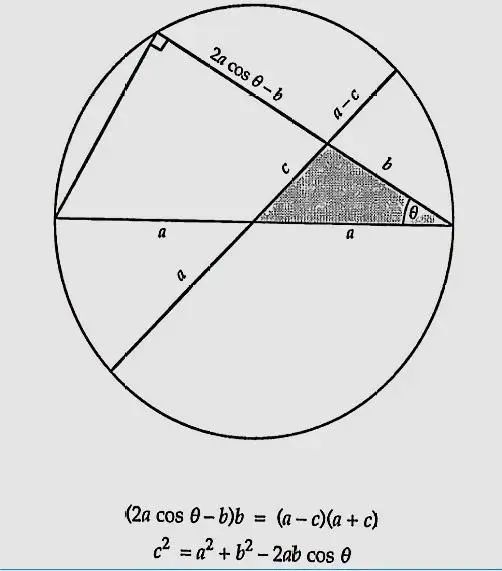
方法十七:余弦定理,当90度角时
方法十八:达芬奇的证明
方法十九:行列式
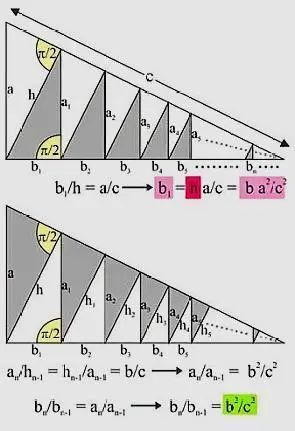
方法二十:无穷级数证明法
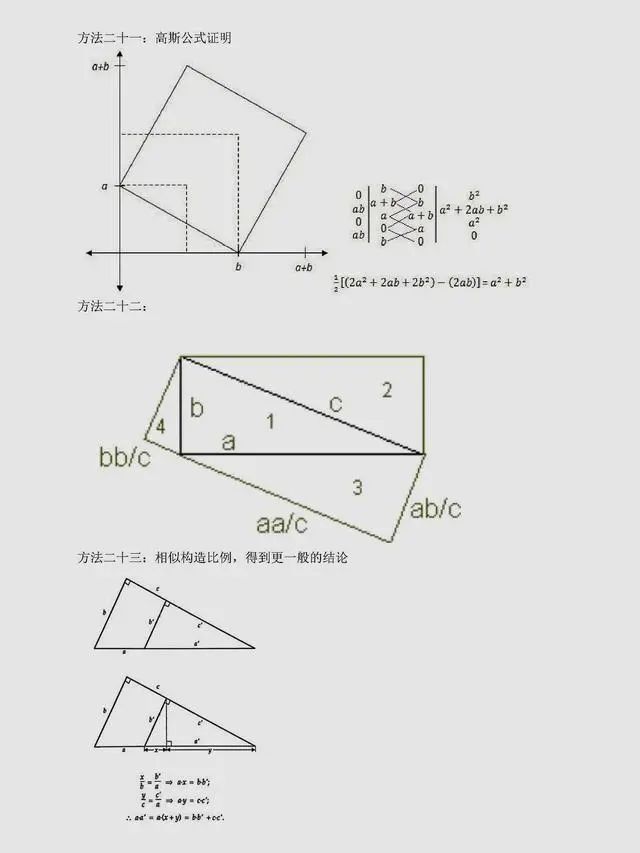
方法二十一:高斯公式证明
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/153990.html