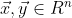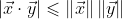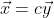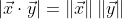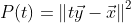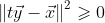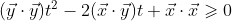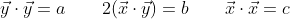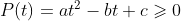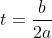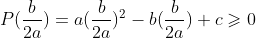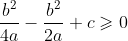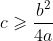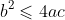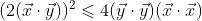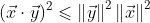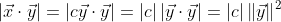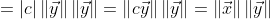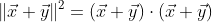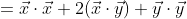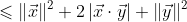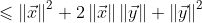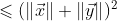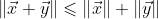五、柯西-施瓦茨不等式及应用

大家好，欢迎来到IT知识分享网。

1. 柯西-施瓦茨不等式

假设

$\vec{x},\vec{y} \in R^n$

且

$\vec{x},\vec{y}$

不为0，那么

$\left | \vec{x} \cdot \vec{y} \right | \leqslant \left \| \vec{x} \right \| \left \| \vec{y} \right \|$

当且仅当

$\vec{x} = c\vec{y}$

时

$\left | \vec{x} \cdot \vec{y} \right | = \left \| \vec{x} \right \| \left \| \vec{y} \right \|$

该不等式称为柯西-施瓦茨不等式，Cauchy Schwarz Inequality，其表示的是向量的点积与向量的长度之间的关系。

2. 不等式证明

假设

$P(t)=\left \| t\vec{y} - \vec{x} \right \| ^2$

因为向量的长度大于等于0，所以

$\left \| t\vec{y} - \vec{x} \right \| ^2 \geqslant 0$

$(t\vec{y}-\vec{x}) \cdot (t\vec{y}-\vec{x}) \geqslant 0$

根据向量点积的交换率、分配率和结合律

$t\vec{y} \cdot t\vec{y} + t\vec{y} \cdot (-1\vec{x}) + (-1\vec{x}) \cdot t\vec{y} + (-1\vec{x}) \cdot (-1\vec{x}}) \geqslant 0$

$(\vec{y} \cdot \vec{y})t^2 -2(\vec{x} \cdot \vec{y})t + \vec{x} \cdot \vec{x} \geqslant 0$

下面做一个替换，目的是简化已展开的不等式，假设

$\vec{y} \cdot \vec{y} = a \uad 2(\vec{x} \cdot \vec{y}) = b \uad \vec{x} \cdot \vec{x} = c$

那么

$P(t) = at^2 -bt + c \geqslant 0$

对于任意的t，上面的不等式均成立，假设

$t=\frac{b}{2a}$

那么

$P(\frac{b}{2a})=a(\frac{b}{2a})^2-b(\frac{b}{2a})+c \geqslant 0$

$\frac{b^2}{4a} - \frac{b^2}{2a} + c \geqslant 0$

$c \geqslant \frac{b^2}{4a}$

因为a不仅非0，而且为正，因此

$b^2 \leqslant 4ac$

将a,b,c重新换成向量的积

$(2(\vec{x} \cdot \vec{y}))^2 \leqslant 4(\vec{y} \cdot \vec{y})(\vec{x} \cdot \vec{x})$

$(\vec{x} \cdot \vec{y})^2 \leqslant \left \| \vec{y} \right \|^2 \left \| \vec{x} \right \|^2$

不等式两边同时开平方

$\left | \vec{x} \cdot \vec{y} \right | \leqslant \left \| \vec{x} \right \| \left \| \vec{y} \right \|$

证明完毕

3. 不等式相等

假设

$\vec{x} = c\vec{y}$

那么

$\left | \vec{x} \cdot \vec{y} \right | = \left | c\vec{y} \cdot \vec{y} \right | = \left | c \right | \left | \vec{y} \cdot \vec{y} \right | = \left | c \right | \left \| \vec{y} \right \|^2$

$=\left | c \right | \left \| \vec{y} \right \| \left \| \vec{y} \right \| = \left \| c\vec{y} \right \| \left \| \vec{y} \right \| = \left \| \vec{x} \right \| \left \| \vec{y} \right \|$

证明完毕

4. 应用–证明三角形两边和大于第三边

$\left \| \vec{x}+\vec{y} \right \|^2=(\vec{x}+\vec{y}) \cdot (\vec{x}+\vec{y})$

$=\vec{x} \cdot \vec{x} + 2(\vec{x} \cdot \vec{y}) + \vec{y} \cdot \vec{y}$

$=\vec{x} \cdot \vec{x} + 2(\vec{x} \cdot \vec{y}) + \vec{y} \cdot \vec{y} = \left \| \vec{x} \right \|^2 + 2(\vec{x} \cdot \vec{y}) + \left \| \vec{y} \right \|^2$

$\leqslant \left \| \vec{x} \right \|^2 + 2\left | \vec{x} \cdot \vec{y} \right | + \left \| \vec{y} \right \|^2$

应用柯西施瓦茨不等式：

$\leqslant \left \| \vec{x} \right \|^2 + 2\left \| \vec{x} \right \|\left \| \vec{y} \right \| + \left \| \vec{y} \right \|^2$

$\leqslant (\left \| \vec{x} \right \| + \left \| \vec{y} \right \|)^2$

不等式两边同时开平方：

$\left \| \vec{x} + \vec{y} \right \| \leqslant \left \| \vec{x} \right \| + \left \| \vec{y} \right \|$

因此，三角形的两边和大于第三边。

为什么要用柯西施瓦茨不等式来证明三角形两边和大于第三边，而不用初中学过的“大角对大边，小角对小边”？因为前者的证明过程可以扩展到n维空间，后者只适用于2维空间。线性代数的美就在于，其理论可以扩展到n维空间。

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/154549.html

五、柯西-施瓦茨不等式及应用

1. 柯西-施瓦茨不等式

2. 不等式证明

3. 不等式相等

4. 应用–证明三角形两边和大于第三边

相关推荐

发表回复