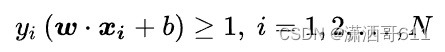支持向量机svm

大家好，欢迎来到IT知识分享网。

线性可分(假设每一个点都分对了）

支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

支持向量：真正发挥作用的数据点，ɑ值不为0的点

（kkt就像求导一样，是取强对偶的必要条件，不过一般当成充要了）

感觉不满足ktt会使w变大

一个简单的例子

需要坐标点那个向量点乘

对aerfa求导，得到aerfa1=1.5         aerfa2=-1

不符合条件。

所以极值在每个aerfa取0时可能得到

最后aerfa1=aerfa3=0.25    aerfa2=0

即x1和x3来发挥作用

作用：选出来离雷区最远的决策边界（雷区就是边界上的点，要Large Margin）

  已知如图超平面且线性可分

几何间隔：（对几维空间都成立）

（几何间隔）恒大于0，不用带绝对值符号。

y（i）是数据点的标签，取+1，或者-1

取几何间隔的最小值，这个距离就是我们所谓的支持向量到超平面的距离。因此，SVM模型的求解最大分割超平面问题可以表示为以下约束最优化问题

一通简单的变换：

得到一个新的式子：

第一个图的+1,-1两条线就是这么来的。这就是一个约束条件。

为了使几何间隔最大，需要w取最小值（很好理解：找到支持向量了，那么w越小，几何间隔就越大）

原问题就变成了：

每一个点都是约束条件 

之后就可以对其使用拉格朗日乘子法得到其对偶问题（对偶问题变量是拉格朗日乘子，一定是凸优化，更加方便）

当样本点不满足约束条件时，将 aerfa设成无线大，所以thrta（w）也无限大

所以得到原函数分段形式

对偶问题：

p和d的联系呢？p>=d，当满足两个条件：

① 优化问题是凸优化问题

（凸优化问题：凸函数 又是凸集

    凸集交集也是凸集

   所以对偶函数一定是凸优化问题

   一般凸优化就是强对偶关系）

② 满足KKT条件

时，等号成立。

证明凸优化一定强对偶

也很好理解！（t是f（x） lamta是拉格朗日乘子）

或者公式来分析！

只有当 G2是一个凸集的时候，等号才会成立。（t是f（x）  u是限制函数）

这里想象一下t和u都是一个三维曲面，它们都是凸集，所以交集也是凸集，然后从三维投影到二维

去掉x轴，仍是凸集。

凸集那么上图可知，一定是强对偶问题。

首先，本优化问题显然是一个凸优化问题

然后是KKT条件：（kkt就像求导一样，是取强对偶的必要条件，不过一般当成充要了）

把上图条件分别标号1-5

这是:4,1,5

松弛意味着lamta为0，该条件无效

 这是：3（把w和b都看成x就好了，我觉得x是除了拉格朗日乘子的其他项）

带入拉格朗日目标函数中，消去w和b ，b自己就没了

把目标式子加一个负号，将求解极大转换为求解极小 

 smo优化算法，最后由aerfa得到结果：

 b=y(j)-wx(j)

过渡

这里加平方主要为了不再引入新的约束条件，如果只引入a（i），会导致a（i）>0

KKT. 的公式推导。（感觉不如我的图直观）

线性不可分（hinge损失）

但是实际情况下几乎不存在完全线性可分的数据，为了解决这个问题，引入了“软间隔”的概念，即允许某些点不满足约束。

一个直观的理解：一万个数据，有一个分错了，那么如果线性可分模型，就会报错。但是如果用hinge损失的话，只会对目标函数有轻微的影响，最后模型会把这个点相当于是忽略了。

这个式子意味着每一个点都在边界线外。如果等于1，那就在边界线上了

以此类推，小于1大于0，意味着点可以分在边界线内部了

就是我们可以为了更大的决策边界来忽视一些边界点

之后为原函数加上惩罚项。

当C趋近于很大时：oumiga必须取很小，意味着分类严格不能有错误
当C趋近于很小时：oumiga可以取很大，意味着可以有更大的错误容忍

 和

等价（好神奇，我想了好久）原来下面这个式子隐藏了一个条件：就是目标函数要取最小值

那么oumiga一定是最小的那个，瞬间就等价了

现在两种限制条件了，所以得两种拉格朗日乘子

之后就是求w和oumiga共同的最小值了。

之后做法差不多：

对oumiga求导，多了一个等式，就是c那个。

大于1，说明就和线性可分没区别了，即oumiga=0；

等于1，说明在决策边界上，和线性也没区别

小于1，在决策边界內部  ，此时，oumiga会把这个点拉回决策边界，需要对目标函数有一个惩罚项来平衡。

不难发现软间隔SVM只是在对拉格朗日乘子阿aerfa的约束上加上了一个上界C。 来减少这个点对整体模型构建的影响。

核函数

低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

 核函数的作用

 高斯核函数意味着无限维度。

映射多了一个z轴，映射到了三维空间，然后切割