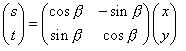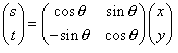坐标系旋转变换公式图解

大家好，欢迎来到IT知识分享网。

1 围绕原点的旋转
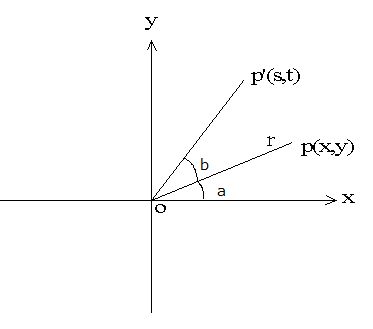
如下图， 在2维坐标上，有一点p(x, y) , 直线opの长度为r, 直线op和x轴的正向的夹角为a。 直线op围绕原点做逆时针方向b度的旋转，到达p’ (s,t) 

s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b)   (1.1)
t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b)  (1.2)
其中 x = r cos(a)  , y = r sin(a)
代入(1.1), (1.2) ,
s = x cos(b) – y sin(b)    (1.3)
t = x sin(b) + y cos(b)    (1.4)

2．座标系的旋转
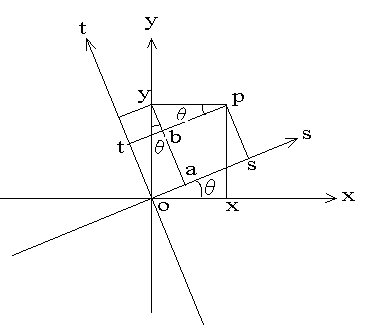
在原坐标系xoy中,  绕原点沿逆时针方向旋转theta度， 变成座标系 sot。
设有某点p，在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。

oa = y sin(theta)   (2.1)
as = x cos(theta)   (2.2)
综合(2.1)，(2.2) 2式
s =  os = oa + as = x cos(theta) + y sin(theta) 
t =  ot = ay – ab = y cos(theta) – x sin(theta)

用行列式表达如下：

而您一旦用以下这图解方法，随时眼见显然，再也不会搞错。