大家好,欢迎来到IT知识分享网。
文章目录
今天,我们来学习一下 塞瓦(
C e v a Ceva Ceva )定理。
C e v a Ceva Ceva 定理究竟是什么
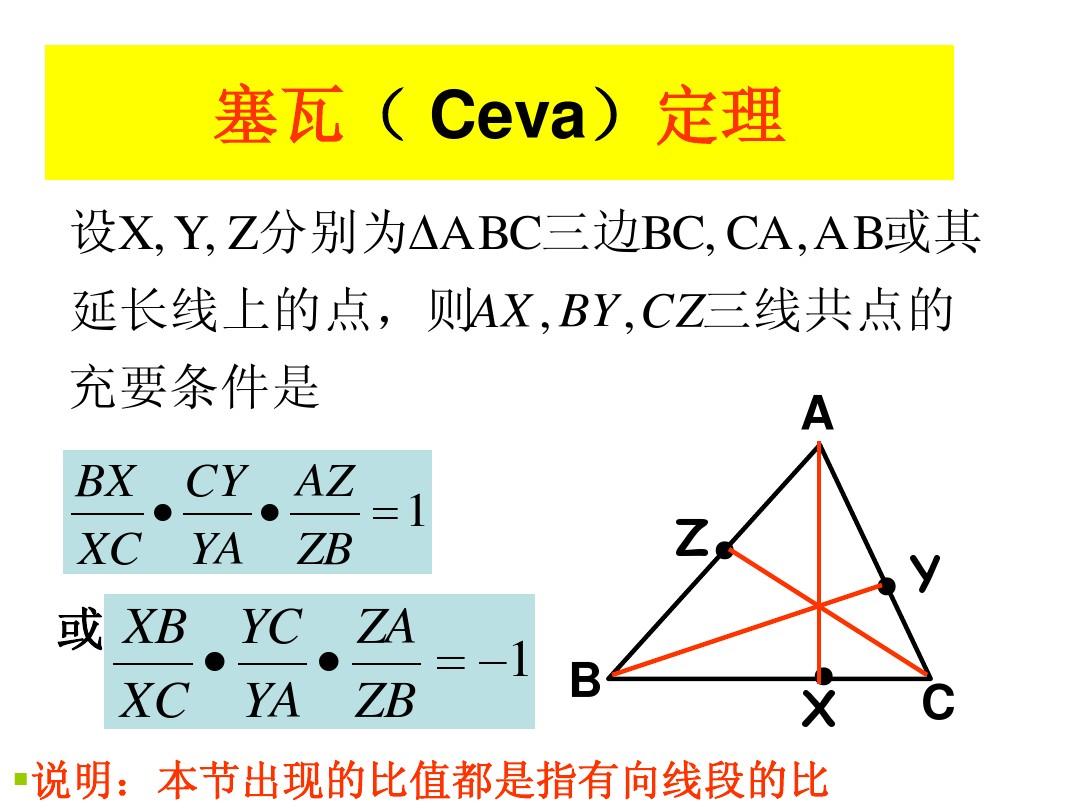
我们来认识一下 C e v a Ceva Ceva 定理(如下图):
如果在这里,你没有学习过向量,那么你可以简单的理解为线段的长度的数值的比值即可(这里我也使用长度了,方便大家理解)。
所以没有学习过向量的同学理解成:
如果在三角形 A B C ABC ABC 中边所在的直线上的点 X , Y , Z X,Y,Z X,Y,Z 有 A X , B Y , C Z AX,BY,CZ AX,BY,CZ 三线共点,那么满足 A Z Z B ⋅ B X X C ⋅ C Y Y A \displaystyle \frac {AZ} {ZB}·\displaystyle \frac {BX} {XC}·\displaystyle \frac {CY} {YA} ZBAZ⋅XCBX⋅YACY 。
如果三角形 A B C ABC ABC 上边所在的直线上的三点 X , Y , Z X,Y,Z X,Y,Z 满足 A Z Z B ⋅ B X X C ⋅ C Y Y A \displaystyle \frac {AZ} {ZB}·\displaystyle \frac {BX} {XC}·\displaystyle \frac {CY} {YA} ZBAZ⋅XCBX⋅YACY ,那么就有 A X , B Y , C Z AX,BY,CZ AX,BY,CZ 三线共点。
为什么要学习 C e v a Ceva Ceva 定理
C e v a Ceva Ceva 定理是我们证明三线共点的主要内容,我们可以通过这个定理来证明许多看起来很难的题目。
C e v a Ceva Ceva 定理的证明
证明: 设三角形 ABC 的外心为 O, A D D B = A E E C \frac{AD}{DB}=\frac{AE}{EC} DBAD=ECAE,则有
举个例子
我们在证明三角形的三条中线交于一点时(如下图):
我们经常使用面积去证明,但是在我们学习了 C e v a Ceva Ceva 定理后,就不需要再那么麻烦了。
现给出 C e v a Ceva Ceva 的证明方法:
我们可知 A F B F ⋅ B D D C ⋅ C E E A = 1 × 1 × 1 = 1 \displaystyle \frac {AF}{BF}·\displaystyle \frac {BD}{DC}·\displaystyle \frac {CE}{EA}=1\times 1\times 1=1 BFAF⋅DCBD⋅EACE=1×1×1=1。
所以,由 C e v a Ceva Ceva 定理可知 A D , B E , C F AD,BE,CF AD,BE,CF 三线共点,得证。(是不是很简单?)
总结 C e v a Ceva Ceva
那么这就是我们的 C e v a Ceva Ceva 定理。是证明三线共点的好方法啊!
寄语(扯个闲篇)
最近信息竞赛快要开始了,在这里我预祝大家能够在 C S P CSP CSP 当中获得好成绩!
作者的 C S P CSP CSP 初赛成绩竟然有 89.5 89.5 89.5 !
祝大家拿到 J / S J/S J/S 一等奖(虽然这个没什么用吧 )
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/155892.html