大家好，欢迎来到IT知识分享网。
0x01 普遍形式
费马素数也叫费马质数。
其中 n 为非负整数。
0x02 历史
法国数学家费马于1640年提出了以下猜想：
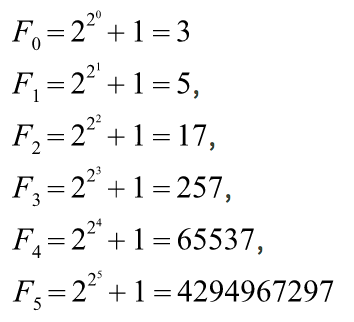
可以看出，前4个是质数，因为第5个数实在太大了，费马认为是质数。
由此提出（费马没给出证明），形如 
的数都是质数的猜想。后来人们就把形如 的数叫费马数。
1732年，欧拉算出第五个费马数 = 641 × 不是质数，宣布了费马的这个猜想不成立，它不能作为一个求质数的公式。
此后人们对更多的费马数进行了研究。
随着电子计算机的发展，计算机成为数学家研究费马数的有力工具。
但即使如此，在所知的费马数中竟然没有再添加一个费马素数。
迄今为止，费马素数除了被费马本人所证实的那五个外没有再发现一个。
实际上，几千年来，数学家们一直在寻找这样的一个能求出所有质数的公式，但直到现在，谁也未能找到这样一个公式，而且谁也未能找到证据，说这样的公式就一定不存在或者这样的公式存不存在，这也就成了一个著名的数学难题。
虽然费马数作为一个关于指数公式的尝试失败了，但有意思的是，1801年数学家高斯证明了如果费马数K为质数，那么就可以用直尺和圆规将圆周K等分。高斯本人就根据这个定理作出了正十七边形。
知乎 – 《高斯作出正 17 边形的依据是什么？》
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/158886.html
