长江上游支流区域洪水频率分析

大家好，欢迎来到IT知识分享网。

《水利水电技术（中英文）》官网网址
https://sjwj.cbpt.cnki.net

摘 要：

在水利水电工程的规划设计中，设计洪水的精度影响着工程的安全性和经济性。区域洪水频率分析能够提高缺资料地区的设计洪水的代表性，为工程建设提供更可靠的数据支持。基于长江上游支流流域35个水文站60 a以上的年最大洪峰流量序列，采用模糊聚类的方法进行水文相似区识别，并选取P-Ⅲ型曲线拟合洪水频率分布曲线，推求长江上游支流的区域洪水频率分布曲线和设计洪水。结果表明，将35个水文站点分为3个区域时满足均匀性检验和一致性检验，分区结果较为合理，分别是雅砻江和大渡河区域、岷江和嘉陵江的中上游区域以及岷江和嘉陵江的中下游区域。以此估计各站点的设计洪水，在0.1%、1%、5%、10%概率下与单站点拟合得到的相对误差平均值分别为12.63%、9.23%、5.76%和3.97%,表明该方法能够用于缺资料地区设计洪水的推求。

关键词：

区域洪水;频率分析;模糊聚类;水文相似性;

作者简介：

丁启(1999—),男，硕士研究生，主要从事水文水资源研究。

*杨汉波(1979—),男，副教授，博士，主要从事水文水资源研究。

基金：

“十四五”国家重点研发项目(2021YFC);

中国长江三峡集团有限公司科研项目资助();

国家自然科学基金项目(U);

水沙科学与水利水电工程国家重点实验室自主课题(2021-KY-04);

引用：

丁启, 杨汉波, 卢韦伟, 等. 长江上游支流区域洪水频率分析[J]. 水利水电技术(中英文), 2022, 53(11): 50- 59.

DING Qi, YANG Hanbo, LU Weiwei, et al. Regional flood frequency analysis in tributaries of the upper reaches of the Yangtze River [J]. Water Resources and Hydropower Engineering, 2022, 53(11): 50- 59.

0 引 言

设计洪水是水利水电工程规划和设计中不可或缺的水文参数，常用计算方法是根据当地水文站点已有的洪水资料直接推求。但该方法需要水文站具有至少20～30 a的水文资料，否则设计洪水的精度可能会达不到设计要求，影响工程的安全性。区域洪水频率分析的方法可有效提高缺资料地区设计洪水的精度，其基本思想是以空间换取时间，即通过引入具有水文相似性的邻近站点的长序列洪水资料，增加缺资料站点的样本信息量，减小短序列洪水资料的偶然性带来的误差，提高设计洪水的精度。

上世纪60年代，标度洪水法这种区域洪水频率分析的经典方法提出后，区域分析的思想就一直被运用在设计洪水的计算中。英国1975年编写的《洪水研究报告》和1999年编写的《洪水估计手册》中建议当样本资料较少时可用区域分析来估计洪水频率分布，美国发布的《洪水流量频率确定指南》中也指出洪水频率分布曲线要用区域平均的方法计算。HOSKING总结了区域洪水频率分析中运用到的基本参数，为后来的研究打下了基础；REZENDE等用线性矩法建立了巴西拉夫拉斯地区缺资料流域的对数正态区域函数，并通过蒙特卡洛模拟达到了95%的置信度，降低缺资料地区洪水的不确定性；KATHERINE等以俄亥俄河流域为例，阐述了一种与气候相关的长期洪水预测方法，并将其推广到了整个美国。

国内在区域洪水分析方面也有较多相关研究。周芬分析了设计洪水的估算方法，认为区域分析是提高设计洪水精度的有效手段；卢韦伟等基于多元分布函数对湘江流域进行了区域分析，其结果在一定程度上为当地设计洪水的计算提供了依据；吴业楠将层次贝叶斯法与区域分析相结合，得到了湘江流域的洪水频率曲线与设计洪水，但是其方法如何与国内常用的P-Ⅲ型分布曲线相结合仍然需要一定的研究；徐磊和林小丽分别以淮河流域和天山北坡为例，验证了线性矩法是推求洪水频率曲线较为有效的方法，提出模糊聚类在水文分区的过程中的优越性；余江游基于指标洪水法得出了淮河流域的区域洪水频率曲线与设计洪水，其方法在计算实测资料较少站点的设计洪水时比传统方法更具有代表性。

长江流域水能资源丰富，同时洪水灾害也频繁发生，但是目前国内对长江流域的区域洪水频率分析较少。莫学海等针对长江流域川江段进行了区域分析，得到了川江流域统一的区域洪水频率曲线，但其研究区域较小，研究站点少，没有较大尺度的数据支撑，结果代表性并不强；徐长江等以P-Ⅲ型分布曲线为研究基础，对汉江流域的16个实测洪水样本开展了研究，得出了区域设计洪水，表明区域洪水频率分析是解缺资料地区设计洪水问题的有效途径，其结果是整个区域的洪水频率曲线，没有针对特定站点求其洪水频率与设计洪水，且缺少与传统方法的对比分析；李立平等以嘉陵江流域为例，选择不同类型的典型年和控制时段，针对流域整体防洪层面开展了设计洪水的研究，得到了多个典型年的设计洪水过程，为流域防洪和雨洪资源化提供了依据。

目前国内推求设计洪水的主要方法仍是由已有洪水资料直接推求。但是我国由于历史原因等因素，许多地区的洪水资料较少，代表性不足，无法直接推求设计洪水。本文收集了长江上游支流流域35个水文站点60余a的最大洪峰流量数据，以指标洪水法为基础，采用比较稳健的线性矩法估计区域洪水频率曲线的参数，以模糊聚类法进行水文相似性分区，简化水文相似性分区指标、消除分区过程中的主观因素，分析并得出最优分区方案，在较大尺度上分析长江上游的区域洪水频率，得出区域洪水频率曲线与设计洪水；最后采用交叉检验法对比区域分析与单站点资料得出的设计洪水之间的相对误差，力求提高缺资料地区设计洪水的代表性。

1 研究区域概况

本文的研究区域主要为长江上游支流流域，包括大渡河流域、岷江流域、嘉陵江流域等。长江上游干流河道全长约4 510 km, 流域面积约100万km2,区域内高山峡谷众多，河流落差大，水能资源丰富，修建有超过19 000座水电站。本文选取长江上游支流流域的35个水文站点为研究对象，其分布如图1所示。

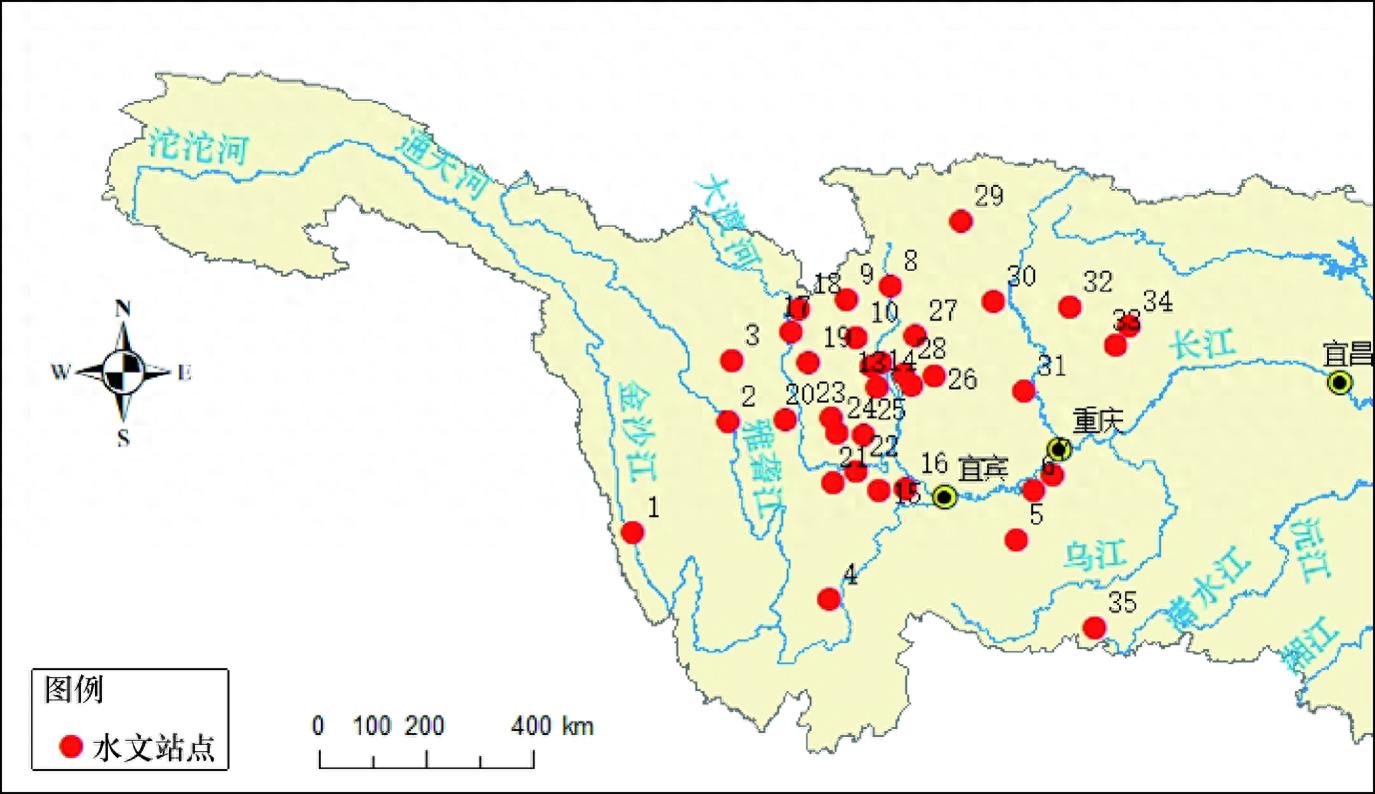
图1 研究区域

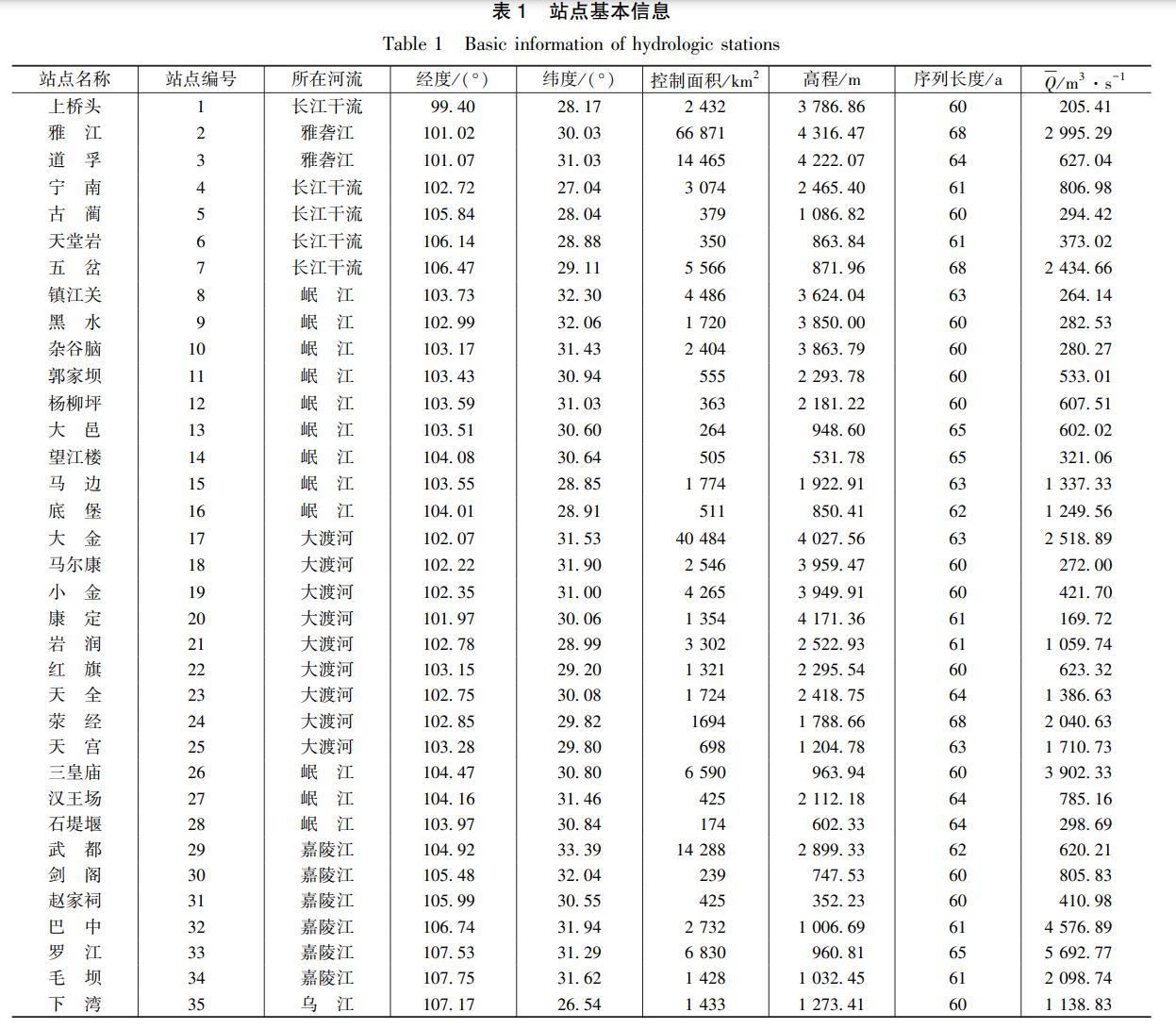
研究数据为35个水文站点从上世纪六十年代到2018年的年最大洪峰流量序列，平均序列长度为62 a, 各水文站点的基本信息如表1所列，表中Q¯指多年平均洪峰流量，数据来源于水利部信息中心。

2 区域洪水频率分析方法

本文以指标洪水法为基础，对长江上游支流流域进行区域洪水频率分析。指标洪水法的思想是：N个洪水频率曲线线型和参数完全一样、仅洪水尺度有差别的水文站可以构成一个水文相似区，其中第i个水文站概率为P的设计洪水为

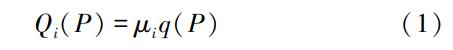
式中，q(P)为区域洪水频率曲线；μi为指标洪水，μi与地形地貌、气候特征、集水面积等多方面因素有关,本文取μi为站点多年洪峰流量序列的均值Q¯i。利用公式Q′ij=Qij/Q¯i(j=1,2,⋯ni)将洪水序列无量纲化，消除水文站洪水尺度不同产生的影响，再用线性矩法计算无量纲序列的线性变差系数(Cv)、线性偏态系数(Cs)和线性峰度系数(Ck)。

本文的研究路线为：检验洪水序列的趋势性，剔除不适宜区域频率分析的站点；进行水文相似区识别，得到具有相似性的站点；进行均匀性检验和一致性检验，检验分区结果是否合理、可靠；最后根据区域综合的洪水频率曲线推求站点设计洪水。研究路线如图2所示。

图2 研究路线

2.1 趋势性检验

区域频率分析要求所研究站点受人类活动影响较小，否则其分布形式会发生变化。本文认为具有趋势性变化的站点即是受人类活动影响较大的站点，采用游程检验法进行趋势性分析，将水文序列具有趋势性的站点从研究中剔除。具体方法为：将洪峰流量序列中小于平均流量Q¯的观测值记为“-”号，其余值记为“+”号，得到符号序列，每一个符号相同的连续序列片段称为一个游程。记序列长度为n,游程总数为r,“+”号和“-”号出现的次数分别为n1和n2,计算其检验参数

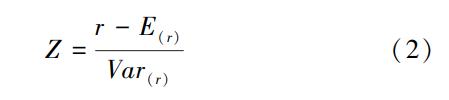
在显著性水平α为0.05的条件下，Z的临界值是|Z0|=1.96,|Z|<|Z0|则认为该序列不具有趋势性。

2.2 水文相似区识别

水文相似区识别的方法有地理位置相近法、流域水文模型法、模糊聚类法等。地理位置相近法是根据自然景观来划分水文分区，具有随意性，而且地理位置相近并不一定代表水文特性相近；而流域水文模型法需要有流域的下垫面条件、植被、土壤等较多方面的数据，分类方法比较复杂。本文采用模糊聚类的方法，以各站点的特征参数为分类依据，计算各水文站点的模糊等价矩阵，消除分区过程中的主观性，可以得出相对客观、合理的分区结果。

假定有n个研究对象，每个研究对象有m个特征值代表其性质，这些特征值组成了原始数据矩阵A=(xij)n*m。对原始数据矩阵进行标准化，得到模糊矩阵A″=(x″ij)n×m,再计算两个研究对象之间的相似程度rij,构造模糊相似矩阵R,其中

对模糊相似矩阵R,存在自然数k(k≤n),使得对于任何大于k的自然数l,恒有Rl=Rk。依次对R求平方，直到Ri=R2i=Ri。Ri,则Ri是R的模糊等价矩阵。其中

对任意i和j,满足0≤cij≤1。在0～1区间内选取适当的λ,将所有小于λ的元素记为0,其余元素记为1,构造等价布尔矩阵，等价布尔矩阵中向量相等的站点即是具有水文相似性的站点。

2.3 均匀性检验

均匀性是指各站点的洪水频率分布曲线线型基本一致。在分区均匀的站点中，某个能反映洪水分布特征的特征值θ应趋近于常数。研究表明，洪水序列的Cv、Cs和Ck能反映洪水的特征，但是考虑Cs和Ck对设计洪水的精度影响很小,其计算方法却十分复杂，故本文以Cv为特征值进行分区均匀性检验。

假定流域有N个站点，第i个站点的序列长度为ni,变差系数为Cv(i),区域平均的变差系数记为Cv(R),计算区域内各站点Cv的离散程度V

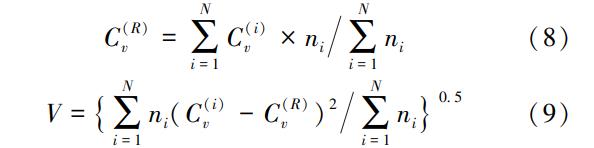
研究表明，水文数据的分布形式与皮尔逊Ⅲ型曲线(P-Ⅲ型曲线)的分布相似程度较高，因此P-Ⅲ型曲线被广泛应用于水文相关计算之中,其概率密度函数为

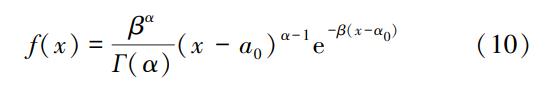
式中，Г(α)=∫∞0xα-1e-xdx,是α的伽马函数；e是自然对数的底数；α是形状参数；β是尺度参数；a0是自变量最小值。

以P-Ⅲ型曲线作为洪水频率曲线线型，区域平均的洪水频率曲线为模拟条件，用蒙特卡洛模拟方法随机模拟水文分区500次，计算每次模拟得到的洪水序列的Cv的离散程度V′,计算500次模拟的V′值的均值μV′和均方差σV′,最后计算检验参数

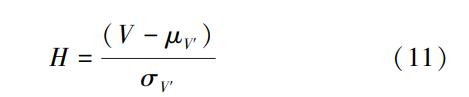
当H<1时，认为分区均匀；1≤H≤2时，认为分区可能均匀；H>2时认为分区不均匀。

2.4 一致性检验

一致性检验是为了找到并剔除与该区域特征值相差较大的站点。以Cv、Cs和Ck作为特征参数，计算检验参数Di,检验分区后区域内站点的一致性，识别出具有较大的差异的站点。记ui=(Cvi,Csi,Cki)T为第i个站点的特征参数向量，记

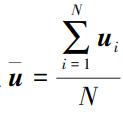
其中N为站点数量。检验参数Di的计算公式为

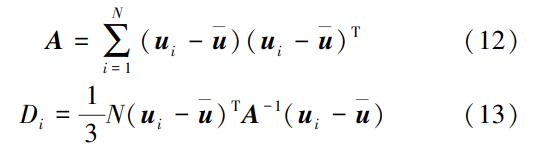
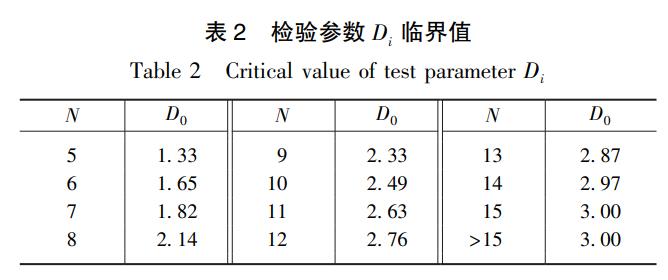
Di小于临界值D0认为该站点与其余站点相差不大。表2是不同N值对应的D0取值。

2.5 估计设计洪水

采用交叉检验法，估算各站点的区域平均设计洪水与单站点设计洪水。假定区域内的某一个站点是缺资料站点，将该站点的洪峰流量序列从区域中剔除，以序列长度为权重对区域内其余站点洪峰流量序列的Cv、Cs加权平均，得到区域平均的C¯v、C¯s,计算区域平均的P-Ⅲ曲线参数

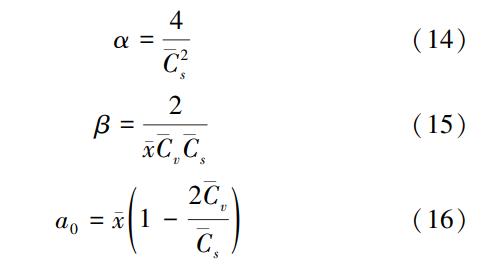
根据公式(1)(10)推求出区域平均设计洪水；再以该站点的特征参数计算单站点的P-Ⅲ曲线，得到单站点设计洪水。对每个站点重复上述操作，评估用区域平均洪水估计缺资料站点的设计洪水的精度。

3 结 果

3.1 趋势性检验

表3给出了这35个站点的检验参数Z。如表3所列，古蔺、镇江关、大金、武都四个站点的|Z|>|Z0|=1.96,在显著水平α为0.05的条件下有趋势性，不满足趋势性要求，将其从本研究中剔除。

3.2 水文相似区识别

选取不同的λ值构造等价布尔矩阵，识别水文相似区。当λ小于0.727时，除黑水站、小金站、康定站、岩润站、荥经站外的站点属于同一区域，而这5个站点各自属于一个区域，当λ逐渐增大，其余站点的分区数量逐渐增大。计算不同情况下的分区均匀性指标H,结果如表4所列，所有分区的H均小于1,表明分区结果是均匀的。

将分区后区域内各站点的Cv、Cs以序列长度为权重加权平均，得到C¯v、C¯s,利用公式(14)—(16)计算P-Ⅲ曲线参数，得到区域平均的洪水频率曲线，绘出不同分区结果下的区域洪水频率曲线如图3所示。

图3 不同分区结果下的洪水频率曲线

计算不同分区情况下的区域平均与单站点设计洪水，分成2个区域时，汉王场站、剑阁站、郭家坝站三个站点的设计洪水与区域平均值相差最大，这三个站点在不同分区结果中1%概率下的区域平均与单站点设计洪水的相对误差如表5所列。

如表5所列，分区数量从2增加到3时，相对误差有较大程度的减小；增加到4和5时相对误差没有变化；分区数量大于3时，雅江站和马尔康站构成了一个区域，站点数量较少，分区的意义不大。故分区数量为3时结果最优，其空间分布如图4所示。

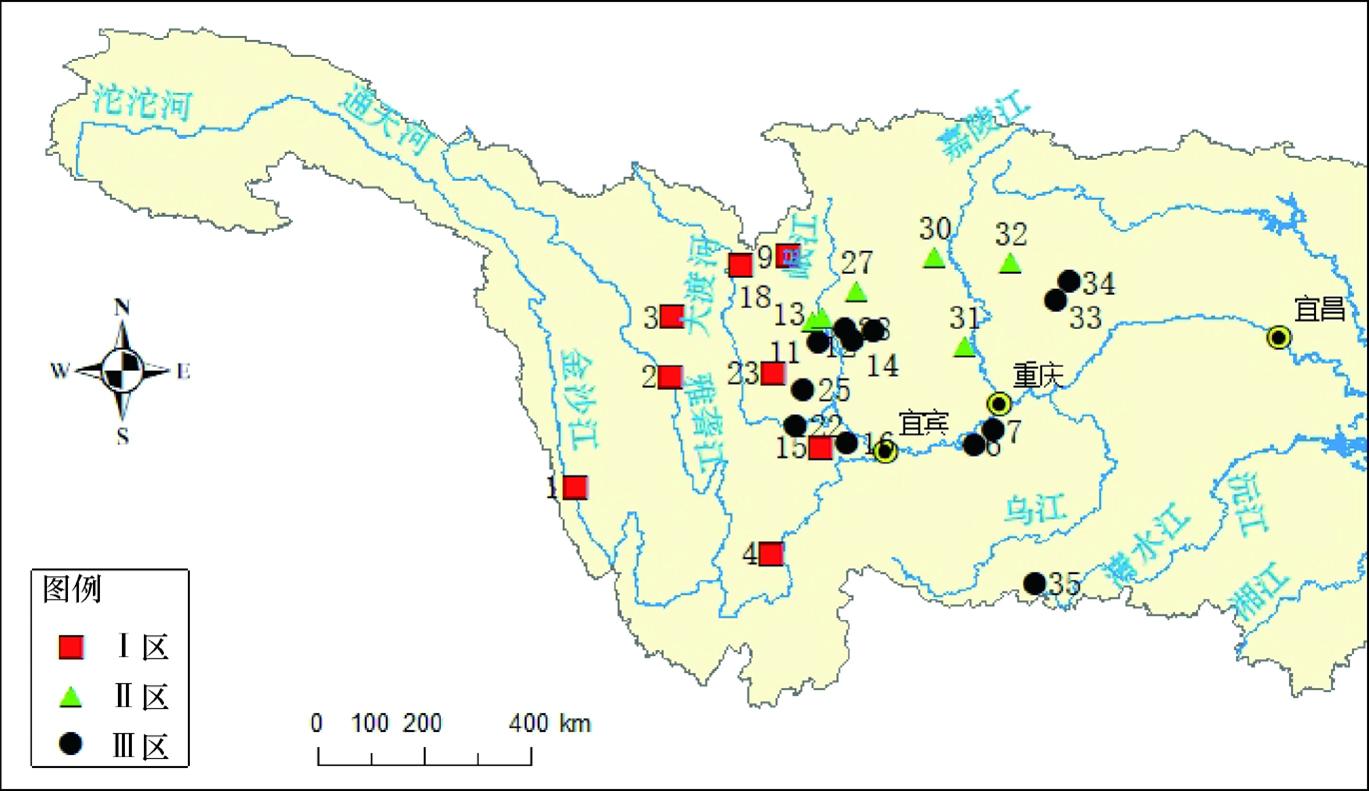
图4 分区数量为3时区域内各站点分布

如图4所示，Ⅰ区域为雅砻江和大渡河区域；Ⅱ区域为岷江和嘉陵江的中上游；Ⅲ区域为岷江和嘉陵江的中下游，其中35号站点与区域内其余站点空间位置上距离较远，但是其海拔(1 273 m)与区域内其余站点的平均海拔(1 168 m)接近。

表6是分成3个区域时各站点的一致性检验参数Di值，如表6所列，各区域内站点的检验参数Di均小于临界值D0,通过了一致性检验。

图5给出了各站点Cv和Cs的空间分布图，Ⅰ区域内的站点的Cv在0.25～0.34之间，Cs在0.39～0.75之间；Ⅱ区域内站点的Cv在0.62～0.87之间，Cs在0.90～2.25之间；Ⅲ区域内站点的Cv在0.39～0.59之间，Cs在0.33～1.88之间。同一区域内站点的Cv比较接近，并且区域之间有比较明显的差异。

图5 各站点Cv、Cs分布

3.3 设计洪水

假定区域内某站点为缺资料站点，用该区域其余站点的平均特征参数计算区域洪水频率曲线，估计该站点的设计洪水，与单站点数据得到的设计洪水进行比较，得到分区数量为3时各站点不同概率下的区域平均设计洪水与单站点设计洪水，如表7所列。

如表7所列，区域洪水频率分析的方法在估计千年一遇洪水时，部分站点可能会存在较大的误差，但是所有站点的误差平均值仅有12.63%;随着估计的洪水逐渐减小，最大误差和误差平均值也随之减小，估计10 a一遇洪水时的最大的误差仅有10.95%,误差平均值仅为4.0%,说明用区域洪水频率分析的方法估计缺资料地区的设计洪水是可行的。

由站点指标洪水和无量纲的区域设计洪水，可以计算出站点的设计洪水。以上桥头站为例，其0.1%概率下无量纲的区域平均设计洪水为2.16,该站点的指标洪水为205.41 m3·s-1,故其0.1%概率下的区域平均设计洪水为2.16×205.41=443.69 m3·s-1。

4 结 论

本文以长江上游支流流域的35个水文站点为研究对象，分析这些站点六十多年的年最大洪峰流量序列，基于指标洪水法进行区域洪水频率分析，得出了以下结论：

(1)本文采用模糊聚类的方法，以洪水序列的变差系数Cv和偏态系数Cs作为聚类因子，采用线性矩法估算参数，以P-Ⅲ曲线拟合洪峰频率曲线，得到长江上游支流3个主要分区以及各区域的洪峰频率曲线，有利于提升长江上游支流区域的设计洪水的精度。

(2)三个主要分区中，Ⅰ区域为雅砻江和大渡河，Ⅱ区域为岷江和嘉陵江的中上游，Ⅲ区域为岷江和嘉陵江的中下游，且同一区域内的各站点地理位置邻近、特征参数相似，说明区域化结果良好。

(3)假定区域内的某个站点为缺资料站点，用区域内其余站点的洪水序列估计该站点的设计洪水，进行交叉检验，得到估计千年一遇的洪水时所有站点的相对误差的平均值为12.63%,且随着估计的洪水重现期减小，相对误差也逐渐降低，说明使用区域分析方法估计缺资料地区的设计洪水是可行的。

本文仍存在部分不足：部分站点在估计小概率洪水时区域设计洪水与单站点设计洪水相差仍然较大，可能是因为缺少历史大洪水数据，导致区域洪水频率曲线在向大洪水外延时缺乏参考。

水利水电技术（中英文）

水利部《水利水电技术（中英文）》杂志是中国水利水电行业的综合性技术期刊（月刊），为全国中文核心期刊，面向国内外公开发行。本刊以介绍我国水资源的开发、利用、治理、配置、节约和保护，以及水利水电工程的勘测、设计、施工、运行管理和科学研究等方面的技术经验为主，同时也报道国外的先进技术。期刊主要栏目有:水文水资源、水工建筑、工程施工、工程基础、水力学、机电技术、泥沙研究、水环境与水生态、运行管理、试验研究、工程地质、金属结构、水利经济、水利规划、防汛抗旱、建设管理、新能源、城市水利、农村水利、水土保持、水库移民、水利现代化、国际水利等。