著名的球谐函数

大家好，欢迎来到IT知识分享网。

球谐函数（Spherical Harmonics）是描述球对称系统中角度分布的数学工具，广泛应用于量子力学、电磁学、计算机图形学等领域。

一、拉普拉斯方程在球坐标系下的分离变量

球谐函数起源于求解 拉普拉斯方程 在球坐标系下的角向部分：

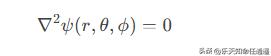
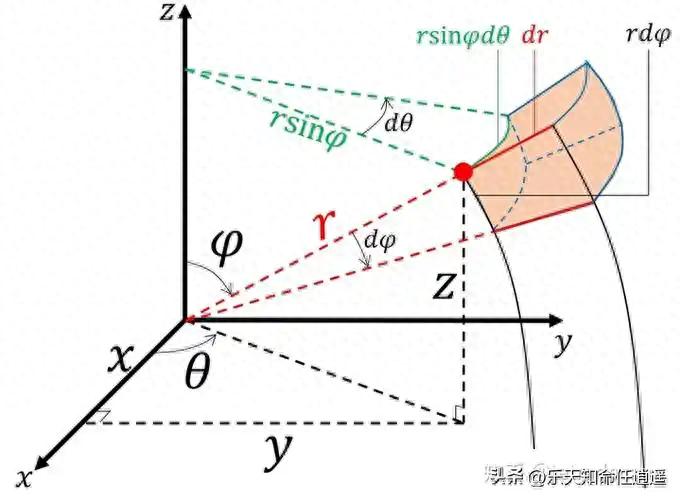
在球坐标系 (r,θ,ϕ)中，拉普拉斯算符展开为：

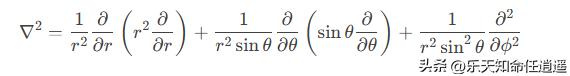
假设解为 分离变量形式：ψ(r,θ,ϕ)=R(r)Y(θ,ϕ)

代入拉普拉斯方程，得径向方程 和 角向方程：

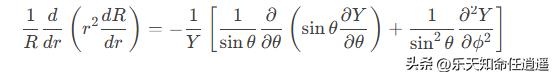
左为径向方程，右为角向方程

即带协变导数ra的形式为：

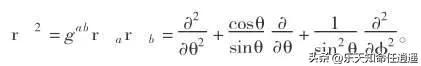
协变导数形式拉普拉斯算符

r²可能的本征值是数-l（l+1），因此令角向方程左右两边等于同一常数 l(l+1)，（l=0，1，3，4……）得到角向方程：

角向方程

角向方程的进一步分离变量:Y(θ,ϕ)=Θ(θ)Φ(ϕ)

代入角向方程：

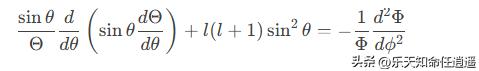
左右两边等于同一常数 m²，得到两个常微分方程：

1. 方位角方程（关于 ϕ）：

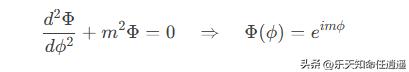
周期性边界条件要求 m为整数。

2、极角方程（关于 θ）：

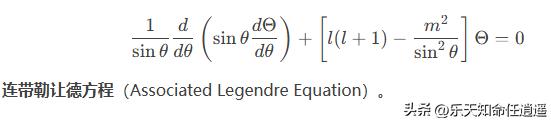
求解连带勒让德方程，得极角方程的解（连带勒让德多项式）：

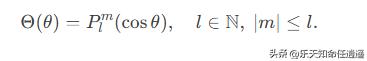
令 x=cos⁡θ，方程转换为标准形式：

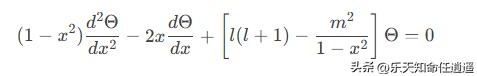
利用齐次常微分方程解法，得连带勒让德多项式：

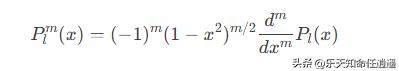
P
l(x)是 勒让德多项式，满足递推关系：

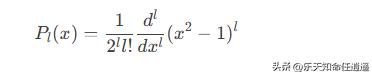
二、归一化与球谐函数的定义

球谐函数需满足 正交归一性：

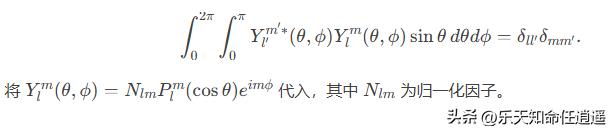
计算归一化因子:

三、球谐函数的最终形式

结合 相位因子（Condon-Shortley 约定）(−1)^m，得到标准定义：

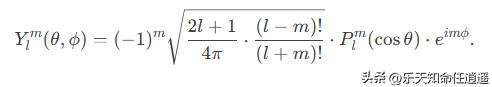
量子数范围：

l=0,1,2,…（角动量量子数）

m=−l,−l+1,…,l（磁量子数）

四、重要性质

1. 正交完备性：
   球谐函数构成 L2(S2) 空间的正交完备基，任何球面函数可展开为：
   

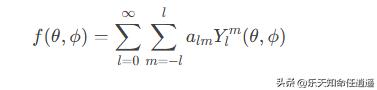
2、对称性：

3、特殊值：

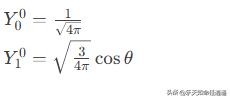
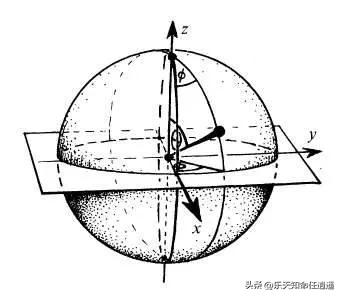
五、几何意义与可视化

球谐函数的模平方

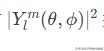
描述角分布：

l=0：各向同性（s轨道）

l=1：哑铃形（p轨道）

l=2：四叶草形（d轨道）

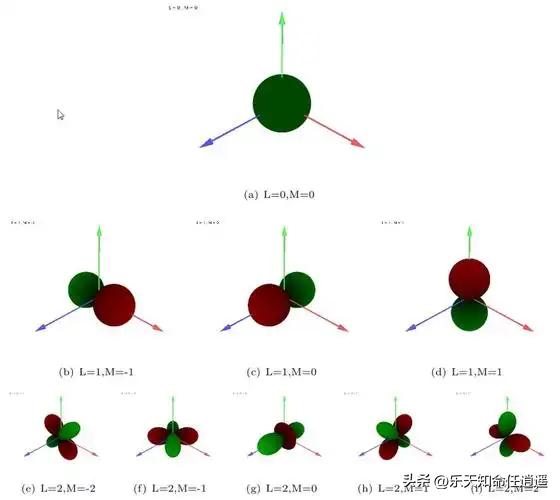
每个 m值对应不同的方位角对称性（例如 m=0绕z轴对称）。

四叶草形

六、应用领域

1. 量子力学：氢原子波函数的角向部分。

2. 电磁学：多极辐射场的展开。
3. 计算机图形学：环境光照的球谐光照模型。
4. 地球物理学：重力场和磁场的数据拟合。

球谐函数的核心思想可总结为： 通过分离变量法分解球对称问题，利用正交多项式构建角空间完备基，最终实现复杂角分布的简洁描述。