初中数学核心突破：实数、平方根与立方根详解

大家好，欢迎来到IT知识分享网。

一、引言：走进实数的世界

同学们，我们学习的数在不断扩展：从数苹果的自然数，到表示欠债的负数，再到不能完整写成分数的小数（比如π）。所有这些数都属于实数。实数就像一条完整的数轴，每一个点都对应一个实数，反之亦然。掌握实数的核心——平方根与立方根，是解开代数、几何难题的关键钥匙！今天，我们就重点攻克这两个重要的概念和它们的运算。

二、实数家族速览

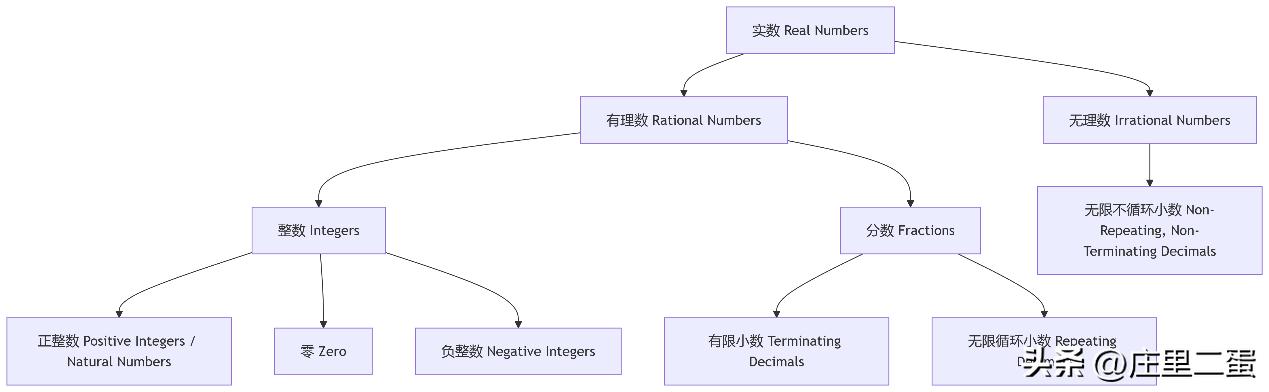
有理数： 能写成分数形式 a/b (a, b 是整数，b ≠ 0) 的数。包括整数、有限小数、无限循环小数。

例子： 5 (=5/1), -0.75 (=-3/4), 0.333… (=1/3)。

无理数： 不能写成分数形式 a/b 的数。小数部分是无限不循环的。

例子： √2 ≈ 1…., π ≈ 3…., √3。

实数 = 有理数 + 无理数

三、核心主角：平方根 (√)（相关概念和性质请参考之前文稿）

平方根的运算方法：

求完全平方数的平方根： 直接利用乘法口诀。

例子： √36 = 6 (因为 6×6=36), √100 = 10。

求非完全平方数的平方根 (化简)：

目标：把根号内的数 a，拆分成一个完全平方数和一个非平方数的乘积 (a = b² × c)。

然后：√a = √(b² × c) = √b² × √c = |b| × √c = b × √c (因为 b ≥ 0)。

例子：

√12 = √(4 × 3) = √4 × √3 = 2√3。

√50 = √(25 × 2) = √25 × √2 = 5√2。

√18 = √(9 × 2) = √9 × √2 = 3√2。

平方根的乘除法：

乘法： √a × √b = √(a × b) (a ≥ 0, b ≥ 0)。

例子： √2 × √3 = √(2×3) = √6； 2√3 × 4√5 = (2×4) × (√3×√5) = 8√15。

除法： √a ÷ √b = √(a ÷ b) (a ≥ 0, b > 0)。

例子： √6 ÷ √2 = √(6÷2) = √3； (10√15) ÷ (5√3) = (10÷5) × (√15 ÷ √3) = 2 × √(15÷3) = 2√5。

平方根的加减法：

核心：只有同类二次根式（根号内相同的数）才能直接相加减。

步骤：

1. 化简每个根式。

2. 合并同类项（系数相加减，根号部分不变）。

例子：

√2 + 3√2 = (1 + 3)√2 = 4√2。 (同类)

√18 + √8 = √(9×2) + √(4×2) = 3√2 + 2√2 = (3+2)√2 = 5√2。 (化简后同类)

√3 + √2 无法再化简！ (不同类)

四、另一主角：立方根 (³√) （相关概念和性质请参考之前文稿）

立方根的运算方法：

求完全立方数的立方根： 利用立方口诀。

例子： ³√8 = 2, ³√27 = 3, ³√(-125) = -5 (因为 (-5)³ = -125)。

求非完全立方数的立方根 (化简)：

目标：把根号内的数 a，拆分成一个完全立方数和一个非立方数的乘积 (a = b³ × c)。

然后：³√a = ³√(b³ × c) = ³√b³ × ³√c = b × ³√c。

例子：

³√16 = ³√(8 × 2) = ³√8 × ³√2 = 2 × ³√2 = 2³√2。

³√54 = ³√(27 × 2) = ³√27 × ³√2 = 3³√2。

³√(-24) = ³√((-8) × 3) = ³√(-8) × ³√3 = (-2) × ³√3 = -2³√3。

立方根的乘除法：

乘法： ³√a × ³√b = ³√(a × b)。

例子： ³√2 × ³√3 = ³√(2×3) = ³√6； 2³√5 × 3³√2 = (2×3) × (³√5׳√2) = 6³√10。

除法： ³√a ÷ ³√b = ³√(a ÷ b) (b ≠ 0)。

例子： ³√6 ÷ ³√2 = ³√(6÷2) = ³√3； (10³√20) ÷ (5³√4) = (10÷5) × (³√20 ÷ ³√4) = 2 × ³√(20÷4) = 2³√5。

立方根的加减法：

核心：只有同类三次根式（根号内相同的数）才能直接相加减。

步骤：

1. 化简每个根式。

2. 合并同类项（系数相加减，根号部分不变）。

例子：

³√5 + 2³√5 = 3³√5。 (同类)

³√16 + ³√54 = 2³√2 + 3³√2 = 5³√2。 (化简后同类)

³√2 + ³√3 无法再化简！ (不同类)

五、平方根 vs 立方根：关键区别总结

六、实数的简单运算

实数的运算规则，我们其实在小学和初一已经学过了很多，只是现在把数的范围扩大到了整个实数（特别是包括了无理数）。核心的运算律依然适用：

核心运算律 (必须牢记！)

1. 加法交换律： a + b = b + a

2. 加法结合律： (a + b) + c = a + (b + c)

3. 乘法交换律： a × b = b × a

4. 乘法结合律： (a × b) × c = a × (b × c)

5. 乘法对加法的分配律： a × (b + c) = a × b + a × c (非常重要！)

具体运算规则

1. 加法与减法：

o 同号相加：绝对值相加，符号不变。 (+a) + (+b) = +(a+b)； (-a) + (-b) = -(a+b)

o 异号相加：绝对值相减（大减小），符号取绝对值大的数的符号。 (+a) + (-b) = ? (看a和b谁大)

o 减法：a – b = a + (-b)。 减去一个数等于加上它的相反数。 这是化减为加的关键！

o 涉及无理数：√2 + 3√2 = 4√2 (合并同类项)。 √2 + √3 无法再化简，结果就是 √2 + √3。

2. 乘法与除法：

o 同号相乘/除：结果为正。 (+a) × (+b) = + (a×b)； (-a) × (-b) = + (a×b)

o 异号相乘/除：结果为负。 (+a) × (-b) = – (a×b)； (-a) × (+b) = – (a×b)

o 除以一个数（不为0）等于乘以它的倒数。 a ÷ b = a × (1/b) (b ≠ 0)

o 涉及无理数：√2 × √3 = √(2×3) = √6。 √2 × √2 = (√2)^2 = 2。 √8 = √(4×2) = √4 × √2 = 2√2 (化简)。

o (3√2) × (4√5) = 3×4 × √2×√5 = 12√10。

o 除法：(6√10) ÷ (2√2) = 6/2 × √10 / √2 = 3 × √(10/2) = 3√5。

3. 乘方：

o a^n 表示 n 个 a 相乘 (n 是正整数)。

o 正数的任何次方都是正数。

o 负数的偶次方是正数，负数的奇次方是负数。

o a^0 = 1 (a ≠ 0)。

o a^{-n} = 1 / a^n (a ≠ 0)。

o 涉及平方根：(√a)^2 = a (a ≥ 0)， √(a^2) = |a| (非常重要！结果一定是非负数)。

运算小贴士

· 运算顺序： 先乘方、开方，再乘除，最后加减。有括号先算括号内！

· 符号是关键： 时刻注意数字前面的正负号。

· 化简： 运算结果要尽量化简。对于无理数，要化简平方根（找到能开出来的平方因子）。

· 计算器： 对于复杂的无理数计算（如 √2 + π），知道概念即可，实际精确值通常保留或估算，计算器可以帮助我们得到近似值。

七、实战演练与避坑指南

1. 经典例题：

计算： √48 – √27 + 2√12

解： √48 = √(16×3) = 4√3； √27 = √(9×3) = 3√3； √12 = √(4×3) = 2√3； 原式 = 4√3 – 3√3 + 2×(2√3) = (4 – 3 + 4)√3 = 5√3。

计算： ³√(-54) + 2³√16

解： ³√(-54) = ³√((-27)×2) = -3³√2； ³√16 = ³√(8×2) = 2³√2； 原式 = -3³√2 + 2×(2³√2) = -3³√2 + 4³√2 = 1³√2。

化简： √(18x⁴y³) (假设 x, y ≥ 0)

解： √(18x⁴y³) = √(9×2×x⁴×y²×y) = √9 × √2 × √x⁴ × √y² × √y = 3 × √2 × x² × y × √y = 3x²y√(2y)。

计算： (√5 + √3)(√5 – √3)

解： 利用平方差公式 (a+b)(a-b)=a²-b²： (√5)² – (√3)² = 5 – 3 = 2。

2. 常见错误陷阱：

混淆平方根与算术平方根： 认为 √9 = ±3 (错！√9 = 3)。平方根有±，但符号√只表示算术平方根（正的）！

忘记 √(a²) = |a|： 计算 √((-5)²) 直接写成 -5 (错！应等于 5 = |-5|)。

不同类根式相加减： 尝试计算 √2 + √3 = √5 (大错特错！无法合并)。

混淆平方根与立方根的性质： 认为负数没有立方根 (错！负数有且只有一个负的立方根)。

运算顺序错误： 如 √4 + 9 误算为 √(4+9)=√13 (错！应先开方后相加：2 + 9 = 11)。牢记运算顺序：括号 > 乘方/开方 > 乘除 > 加减。

分母有理化遗漏： 如 1 / √2 应化简为 √2 / 2。

八、给初中生的高效学习策略

1. 夯实概念基础： 务必清晰区分平方根、算术平方根、立方根的定义、记法和本质区别。理解 √(a²) = |a| 和 ³√(a³) = a 这两个核心公式。

2. 掌握化简技巧：

平方根： 找根号内最大的平方因子 (4, 9, 16, 25, 36…)。

立方根： 找根号内最大的立方因子 (8, 27, 64, 125…)。

目标是把根号内能开出来的部分开出来。

3. 牢记运算规则：

乘除法： 根号外系数乘除，根号内被开方数乘除 (√a √b = √(ab), ³√a ³√b = ³√(ab))。这是简化计算的关键！

加减法： 只合并同类根式！ 化简是合并的前提。

4. 善用数轴： 在数轴上标出 √2, √3, ³√2 等的大致位置，加深对无理数大小的直观理解。

5. 刻意练习：

从简单的完全平方数/立方数的开方练起。

大量练习化简 (√12, ³√24 等)。

练习混合运算，特别注意运算顺序和符号。

练习涉及平方根、立方根的代数表达式化简。

6. 用好错题本： 把练习和考试中做错的关于平方根、立方根的题目记录下来，分析错误原因（概念不清？运算规则错？化简不到位？符号错？），定期复习。

7. 理解应用： 思考平方根、立方根在生活中的应用场景，如：

已知正方形面积求边长（开平方）。

已知正方体体积求棱长（开立方）。

勾股定理计算斜边（开平方）。

理解手机屏幕尺寸（对角线长度，涉及平方根计算）。

九、结语

平方根和立方根是实数王国中充满力量但也需要细心驾驭的成员。它们看似复杂，但只要掌握了概念的核心区别（特别是算术平方根的非负性和立方根对负数的包容性），熟练运用化简技巧和运算规则（乘除合并根号内、加减只认同类项），并辅以持续、有目标的练习，你一定能攻克这个重要堡垒！记住，每一次化简和计算的练习，都在为你在代数、几何乃至更高阶数学的道路上铺就坚实的基石。加油，未来的数学之星！