大家好,欢迎来到IT知识分享网。
1. 向量空间
向量空间表示一整个空间的向量,但不是任意向量的集合都能被称为向量空间。向量空间必须满足一定规则:该空间对空间内向量的线性组合(相加,数乘)封闭。也就是说如果一个向量集合所组成的空间满足两种操作(数乘、相加)且通过这两种操作及他们之间的线性组合后的向量仍然在这个集合所形成的空间中。那么我们就称它为向量空间。比如:v,w为向量空间内的向量,则向量3v 或 v+w 都仍然在此空间中,那么这个空间可称为向量空间。
比如 ![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
很明显,![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
同样,可以通过到三维向量空间![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
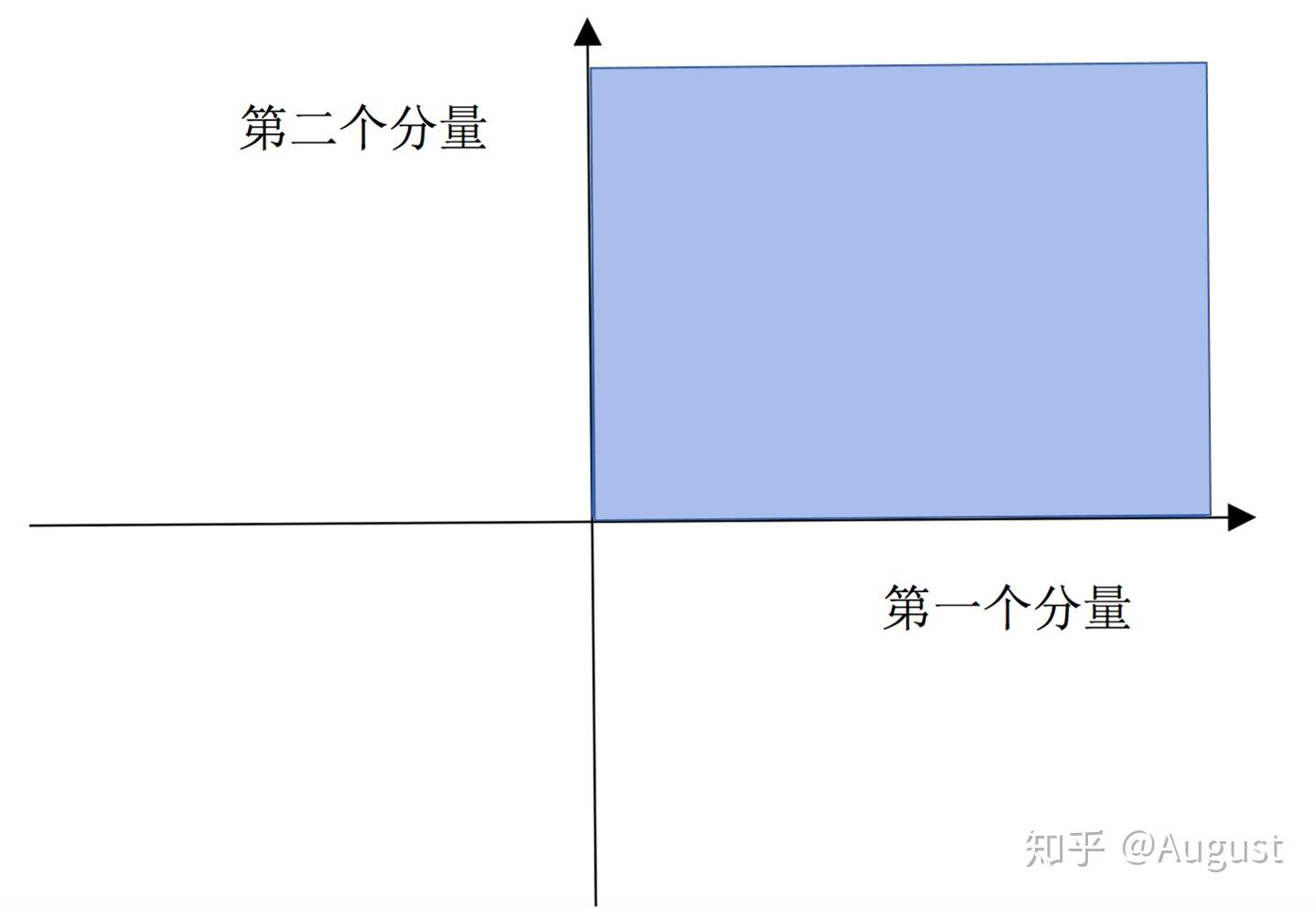
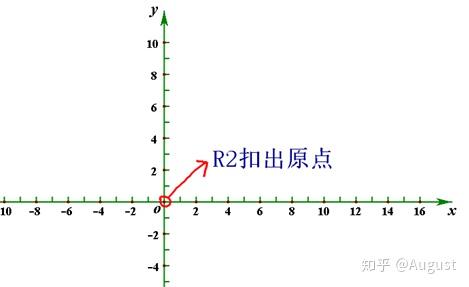
在上面图中,我们可以看到当我们尝试用-1和其中某个向量(除零向量)相乘时,其所得的向量一定不在第一象限中。可见,不满足数乘运算。所以,不是向量空间。
上图中是 ![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
2. 子空间(subspace)
对于子空间,一个很好的解释属于向量空间的一部分,但是它同样满足向量空间的规则,也是一个向量空间。例如在 ![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
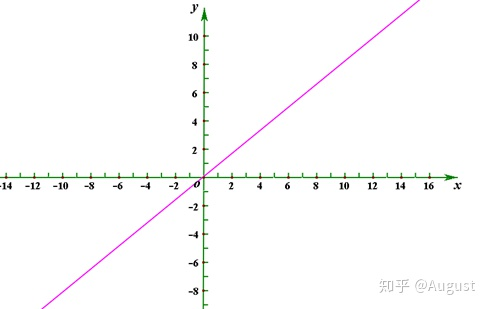
下面让我们去列举下在 ![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
本身
- 任何一条过原点(0,0)的直线(它就像
一样,却不同于
)
- 零向量
R^ 3中的子空间有:
本身
- 任何一个过原点(0,0,0)的平面
- 任何一条过原点(0,0,0)的直线
- 零向量
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
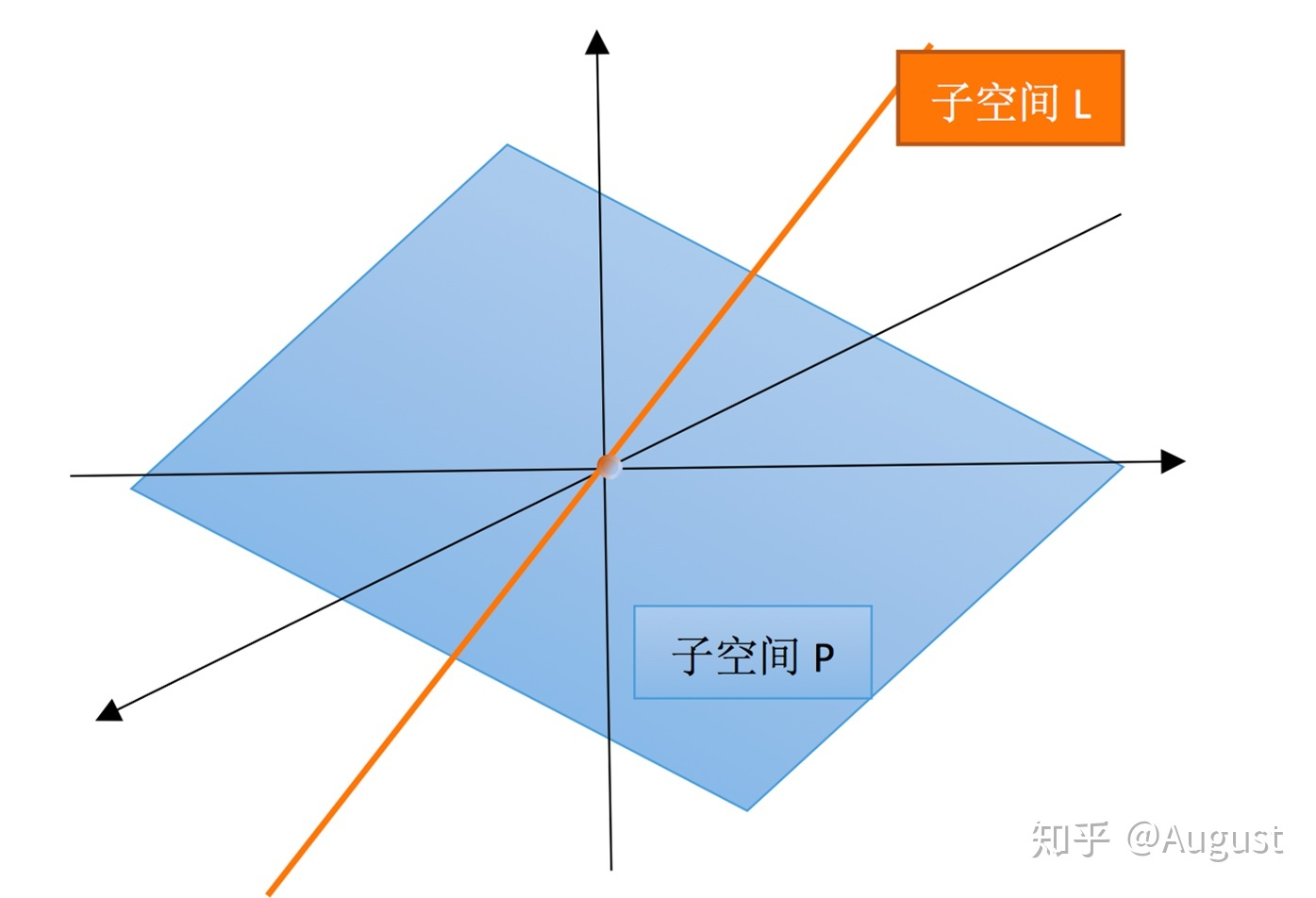
注意:子空间必须包含原点(零向量)
3. 矩阵的列空间(column space)
列空间是由一个矩阵的列向量所构造的子空间,下面我们给出一个矩阵A:
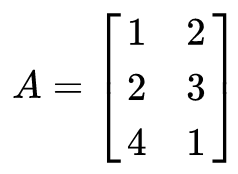
那么矩阵的两个列向量 ![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
因为![向量空间_向量空间知识点总结插图1 [公式]](https://haidsoft.com/wp-content/uploads/2022/11/2022112316405970.jpg)
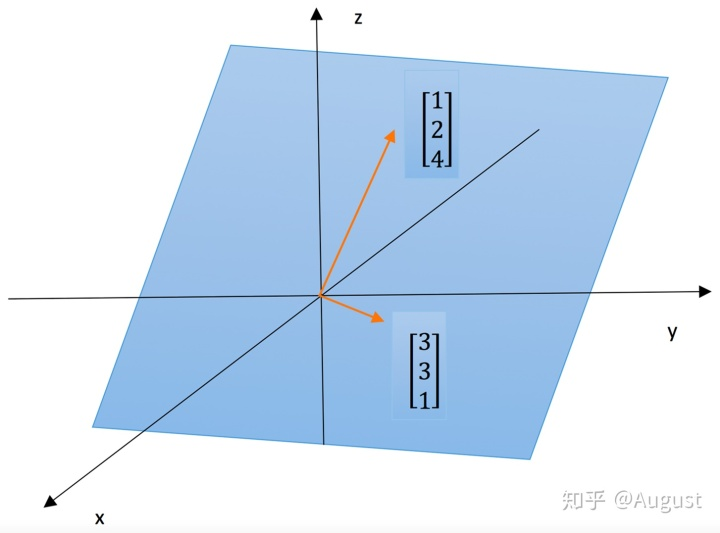
这里还要注意,如果矩阵的列向量两两之间是共线的,其列空间就是一条过原点的直线。
作者:August
链接:https://zhuanlan.zhihu.com/p/44099504
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/29924.html