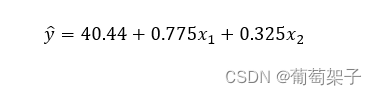响应曲面设计（基本原理）

大家好，欢迎来到IT知识分享网。

一、响应曲面简介

1.1 概括

响应曲面设计（Response Surface Methodology, RSM）是一种统计和数学方法，用于优化工程和科学问题中的多个变量影响。通过这种方法，研究人员能够找到影响某一特定响应（输出变量）的最佳组合条件。RSM通常用于工业过程优化、产品开发和质量改进等领域，其目的是在尽可能少的实验次数内，通过建立响应变量和一个或多个影响因子（自变量）之间的关系，来优化这些影响因子。我们知道正交设计是以线性模型为基础的，因子水平整齐，但是当响应达到最优点附近，需要进行细致的优化时，会出现下列问题：

1. 非线性问题：正交设计主要基于线性假设，但在最优点附近，响应对因素的依赖往往变得非线性。这意味着原有的线性模型可能无法准确描述响应变量与因素之间的真实关系，因而难以精确找到最优点。
2. 因子水平的局限性：正交设计中的因子水平是预先设定的，且通常是均匀分布的。当需要进行更细致的优化以寻找精确的最优条件时，预设的水平可能无法覆盖最优点，或者最优点可能位于两个预定水平之间，导致无法直接通过现有水平组合达到最优。
3. 交互效应的复杂性：在最优点附近，因素之间的交互效应可能变得更加显著和复杂。正交设计虽然可以评估因素的交互作用，但在面对高阶交互或非线性交互时，可能无法提供足够的灵活性和准确性。
4. 细节探索的不足：正交设计优化到一定阶段后，进一步提高响应变量的性能增益变得更加困难。这时，需要更密集的实验设计来细致探索最优条件附近的响应变化，正交设计在这方面的能力有限。

为了解决这些问题，我们需要转向更灵活且能够处理非线性关系的实验设计方法，如响应曲面方法（RSM）或自适应设计。这些方法允许在实验过程中调整因素水平，更好地探索和优化非线性响应面，尤其是在接近最优条件时。

响应曲面设计的核心步骤：

1. 实验设计：首先，使用适当的实验设计方法（如中心复合设计（CCD）或Box-Behnken设计）来收集数据。这些设计通过系统地改变输入变量，允许研究人员评估变量之间的交互影响以及它们对响应的影响。
2. 模型拟合：收集到的数据用于拟合一个近似模型，通常是二次模型，以描述响应变量与一个或多个自变量之间的关系。这个模型可以帮助预测在变量空间中任何点的响应。
3. 分析和优化：利用拟合的模型，通过分析确定那些对响应有显著影响的因素，并找到使响应达到最优（最大化或最小化）的条件。这一步也包括了检验模型的适用性和预测能力。
4. 验证实验：在找到理论上的最优条件后，进行实际实验来验证模型的预测是否准确。

一个简单的应用实例：

假设一个化学制造过程需要优化，目标是最大化某种化学品的产量。影响产量的因素包括反应温度、反应时间和原料A的浓度。通过响应曲面设计，可以系统地改变这些因素，收集数据，并拟合一个模型来描述产量与这些因素的关系。通过分析，研究人员可能发现最高产量出现在特定的温度、时间和浓度下。最后，通过在这些条件下进行实验，可以验证模型的预测是否准确。

响应曲面设计是一种强大的工具，能够有效地指导实验设计和过程优化，节省时间和成本，提高产品质量和生产效率。

1.2 原理

与一阶响应曲面相应的等高线是一组平行直线，最速上升就是按平行于响应曲面等高线的法线方向，一般取通过设定区域的中心且垂直于拟合曲线等高线的直线为最速上升路径，这样，沿着路径的步长就和回归系数(β_i)成正比,实际步长视实际情况决定。
还是举例说明：

二、实例说明

t为为时间，T为温度

用来收集这些数据的设计是增加五个中心点的2²析因设计。在中心点处的重复观察值是用来估计实验误差的，并可以用来检验一阶模型的适合性。过程的当前运行条件在设计的中心点出。
用二水平设计法，以一阶模型进行最小二乘拟合，求得以下模型（其实计算跟二因子析因实验一致，但是也不用了解，实验的时候不用我们计算）：

以中心点的5次实验观测值为重复实验结果，可求出标准偏差估计量，根据2₂析因设计模型可求得交互作用效应，然后对二者进行F检验，这个例子中的交互效应计算出来可以忽略，因此没写。该式子表明最速上升路径为沿x₂方向每移动0.325个单位，则应沿x₁方向移动0.775个单位。
以设计中心点（x₁=0，x₂=0）为起点，若以5min反应时间为基本步长，由上述 t 与x₁的关系式，可知规范变量的步长为Δx₁=1，这个可以这样理解，在关系式中，x₁=（t-35）/5中，t的取值为30—40，如果步长为5min,那么只有三个数，30、35、40对应的x₁分别为-1、0、1，间隔是1，所以步长为1，根据模型系数，Δx₂=（0.325/0.775）Δx₁=0.42，下表列出了新的试验点的规范变量和相应自然变量的值以及根据这些变量取值所得到的实验结果。在实验中（响应y）可以看出，直到第十步，所得到的的观测值都是增加的，而此后开始下降，因此，应该在该点附近（t=85,T=175）进行新的拟合。

应该注意到，这里是一阶模型拟合，如果在实验中，检验结果表明不符合一阶模型，就应该用二阶模型。下次讲二阶。