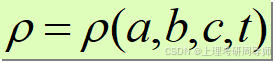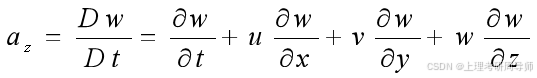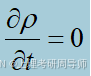【流体力学】第三章 流体运动学基础

大家好，欢迎来到IT知识分享网。

 上理考研周导师的哔哩哔哩频道

我在上面讲课哦

目录

第三章 流体运动学基础

3.1描述流体运动的两种方法

描述流体运动的方法

拉格朗日法   

欧拉法

一元、二元、三元流动模型

一维流动

二维流动

3.2物质导数

欧拉法

3.3迹线、流线和染色线，流管

染色线

3.4流体微团的运动和变形

第三章 流体运动学基础

3.1描述流体运动的两种方法

3.2物质导数

3.3迹线、流线和染色线，流管

3.4流体微团的运动和变形

3.1描述流体运动的两种方法

    在流体静力学中，我们讨论了流体处于平衡状态下的一些力学规律，如压力分布规律，及流体对固体壁的作用力等。但实际上，流体的静止总是相对的，运动才是绝对的。流体最基本的特性就是它的流动性，因此，进一步研究流体的运动规律便更为重要。

   流体运动学主要是研究运动参数（速度、加速度等）随空间位置和时间的变化规律。

描述流体运动的方法

流体只能在固体壁面所限制的空间内外进行运动；

流场 —— 充满运动流体的空间称为流场

 连续介质模型的引入，使我们可以把流体看作为由无数个流体质点所组成的连续介质，并且无间隙地充满它所占据的空间。

流场中流体质点的连续性决定表征流体质点运动和物性的参数（速度、加速度、压强、密度等）在流场中也是连续的。并且随时间和空间而变化。

二. 描述流体运动的方法

假如你是一名篮球教练，防守中该如何掌控整个篮球场？

跟踪：盯人战术      ： 用五名己方球员分别对对方球员进行一对一的跟踪防守。

    布哨：联防战术          ： 用己方五名球员对防守半场进行分区监管，一人负责一片区域的防守。

 根据着眼点的不同，流体力学中研究流体的运动也有两种不同的方法，一种是拉格朗日（Lagrange）方法，另一种是欧拉（Euler）方法。

跟踪：拉格朗日法          ：着眼于流体质点，跟踪质点描述其运动历程

布哨：欧拉法    ：着眼于空间点，研究质点流经空间各固定点的运动特性

拉格朗日法   

拉格朗日法又称随体法着眼于流体质点，跟踪个别流体质点，研究其位移、速度、加速度等随  时间的变化情况，综合流场中所有流体质点的运动

流场中全部质点都包含在（a,b,c）的变数中

t0 时刻:跟踪个别流体质点(a,b,c)

t时刻:质点从(a,b,c)运动到（x,y,z）

(a,b,c) 是拉格朗日变数，即  t=t0 时刻质点的空间位置，用来对连续介质中无穷多个质点进行编号，作为质点标签。

注意：当（a,b,c）变化时，这就表示全部质点随时间的位置变动函数。当t变化时，便是质点（a,b,c）运动轨道的参数方程          

自变量（a,b,c,t）称为拉格朗日变数  

流体在运动过程中其它运动要素和物理量的时间历程也可用拉格朗日法描述，如速度、密度等：

拉格朗日法的缺陷

   在使用拉格朗日法时必须找到 x(a,b,c,t); y(a,b,c,t); z(a,b,c,t)等的函数形式，即跟踪每一个质点进行研究。由于流体具有易流动性，对每一个质点进行跟踪是十分困难的。因此，除了在一些特殊情况（波浪运动。水滴等的运动时），很少采用拉格朗日法。

欧拉法

通过描述物理量在空间的分布来研究流体运动的方法。

着眼于研究空间固定点的情况

选定某一空间固定点，记录其位移、速度、加速度等随  时间的变   化情况，综合流场中许多空间点随时间的变化情况

注意：分析流动空间某固定位置处，流体运动要素（速度、加速度）随时间变化规律，不同时刻不同的流体质点通过空间某一点，分析流体质点从某一空间位置转移到另一位置，运动要素随位置变化的规律，同一流体质点在不同时刻经过空间不同点，欧拉法并没有直接给定流体质点的运动轨迹

  欧拉法是流场法，它定义流体质点的速度矢量场为：，(x,y,z) 是空间点（场点）。流速V 是在 t 时刻占据(x,y,z) 的那个流体质点的速度矢量。

   流体的其它运动要素和物理特性也都可用相应的时间和空间域上的场的形式表达。如加速度场、压力场等：

  欧拉法把流场的运动要素和物理量都用场的形式表达，为在分析流体力学问题时直接运用场论的数学知识创造了便利条件。

采用欧拉法，加速度是一阶导数，而拉格朗日法，加速度是二阶导数（见下文），所得的运动微分方程分别是一阶偏微分方程和二阶偏微分方程，在数学上一阶偏微分方程比二阶偏微分方程求解容易。

在工程实际中，并不关心每一质点的来龙去脉。

 欧拉法在流体力学研究中广泛被采用。两种描述流体运动的方法之间可以相互转换。

定常流和非定常流

若流场中各空间点上的任何运动要素均不随时间变化，称流动为定常（恒定）流。否则，为非定常（非恒定）流。

恒定流中，所有物理量的欧拉表达式中将不显含时间，它们只是空间位置坐标的函数，时变导数为零。

例如，恒定流的流速场：

 恒定流的局部加速度为零，但位变加速度可以不为零。

流动是否恒定与所选取的参考坐标系有关,因此是相对的概念。

均匀流、非均匀流

判别：

若某一时刻流场中各空间点上的物理量都相等，则称均匀场（流），否则为非均匀场（流）。

也即梯度为0：

一元、二元、三元流动模型

一元流（一维流）

    当流速和性能参量的变化仅与一个坐标变量有关的流动。u＝f（s）     s：是流动方向上的位置坐标。这个模型的实质是忽略流速和压强参量等沿主流的横向变化。

二元流（二维流）

  当流动中的速度和性能参量与坐标中某一方向的变量无关时，且在这个方向上的分量也不存在的流动,就叫二元流或称为平面流。

三元流（三维流）

  用欧拉法描述流动，虽然经过恒定流的简化去掉了时间变量，但仍存在x，y，z三个空间变量。这种在流场中的速度和性能参量由三个坐标变量来描述的流动就叫三元流，也称为空间流动。在实际情况下，多数的流动都是三元流，但是，这种流动模型太复杂了，我们是很难求解的。

一维流动 二维流动 三维流动

分为平面流动

轴对称流动

任何实际流动从本质上讲都是在三维空间内发生的，二维和一维流动是在一些特定情况下对实际流动的简化和抽象，以便分析处理。

一维流动

流动要素只取决于一个空间坐标变量的流动

其流场为

s — 空间曲线坐标

元流是严格的一维流动，空间曲线坐标 s  沿着流线。在实际问题中，常把总流简化为一维流动。

二维流动

  流场与某一空间坐标变量无关，且沿该坐标方向无速度分量的流动。

直角系中的平面流动：

大展弦比机翼绕流

3.2物质导数

  速度是同一流体质点的位移对时间的变化率，加速度则是同一流体质点的速度对时间的变化率。

  通过位移求速度或通过速度求加速度，必须跟定流体质点，应该在拉格朗日观点下进行。

拉格朗日法

拉格朗日方法中，某一时刻，任一流体质点的位置可表示为：

   式中a、b、c为初始时刻任意流体质点的坐标，即不同的a、b、c代表不同的流体质点。对于某个确定的流体质点，a、b、c为常数，而t为变量，则得到流体质点的运动规律。对于某个确定的时刻，t为常数，而a、b、c为变量，得到某一时刻不同流体质点的位置分布。通常称a、b、c为拉格朗日变量，它不是空间坐标的函数，而是流体质点标号。

拉格朗日法

质点（a,b,c）的速度和加速度为：

求导时a,b,c 作为参数不变，意即跟定流体质点

注意，流体的密度、压强和温度也可写成类似的函数形式。

欧拉法

欧拉法中，任一空间点处速度场可表示为：

   其中变量x,y,z,t称为欧拉变量，其中 x，y，z有双重意义，一方面它代表流场的空间坐标，另一方面它代表流体质点在空间的位移。当参数x，y，z不变而改变时间t，则表示空间某固定点的速度随时间的变化规律。当参数t不变，而改变x，y，z，则代表某一时刻，空间各点的速度分布。

  根据流体连续介质假设，每一个空间点上都有流体质点所占据。而占据每一个空间点上的流体质点都有自己的速度，有速度必然产生位移。也就是说，空间坐标x，y，z也是流体质点位移的变量，它也是时间t的函数：            x= x (t)      y= y (t)     z= z (t)

流体质点的运动轨迹方程

    上式对时间求导就流体质点沿运动轨迹的三个速度分量：

   加速度定义为在dt时刻内，流体质点流经某空间点附近运动轨迹上一段微小距离时的速度变化率，于是可按复合函数的求导法则，分别将(1)式中三个速度分量对时间取全导数，并将(2)式代入，即可得流体质点在某一时刻经过某空间点时的三个加速度分量：

用欧拉法描述，处理拉格朗日观点的问题。

V也可为流体密度、压强和温度等任一物理量（矢、标）。

   物质导数是反映流体质点某一物理量对时间的变化率，即观察者随流体质点一起运动时看到的物理量变化率。也可称为质点导数或随体导数。物质导数本质上是拉格朗日观点下的概念。

例子

流体不可压是指流体质点的密度运动过程中不变，即

流体均质，则

若流体既均质，同时不可压，则

流体密度场定常，其不是空间坐标和时间的函数，即

3.3迹线、流线和染色线，流管

迹线

迹线是流体质点运动的轨迹，是与拉格朗日观点相对应的概念。

拉格朗日法中位移表达式

即为迹线的参数方程。 t 是变数，a,b,c 是参数。

在欧拉观点下求迹线，因须跟定流体质点，此时欧拉变数x ,y, z成为 t 的函数，所以迹线的微分方程为：

 这是由三个一阶微分方程组成的方程组，未知变量为质点位置坐标(x, y, z)，它是 t 的函数。给定初始时刻的位置坐标，就可以积分得到迹线

根据定义，流线的微分方程为：

其中

实际上这是两个微分方程，其中t是参数。可求解得到两族曲面，它们的交线就是流线族

  根据流线的定义，可以推断：除非流速为零或无穷大处，流线不能相交，也不能转折。

在非定常流情况下，流线一般会随时间变化。在定常流情况下，流线不随时间变，流体质点将沿着流线走，迹线与流线重合。

  迹线和流线最基本的差别是：迹线是同一流体质点在不同时刻的位移曲线，与拉格朗日观点对应，而流线是同一时刻、不同流体质点速度矢量与之相切的曲线，与欧拉观点相对应。即使是在定常流中，迹线与流线重合，两者仍是完全不同的概念。

染色线

染色线是指试验中，利用流场显示技术通过在流场中固定点连续不断注入有色物质所形成的色线（或烟线）。它实际是一段时间内相继经过流场中同一空间点 的流体质点在某瞬时连接起来得到的一条曲线，其形状和结构可反映流场结构和流动特点，也称之为脉线。

染色线既不是流线，也不是迹线。

 定常流动条件下：染色线与流线、迹线重合。

 非定常流动条件下：染色线、流线、迹线互不重合。

3.4流体微团的运动和变形

考察和分析流体质点之间的相对运动

谈及相对运动就必须把讨论问题的尺度从流体质点扩大到流体微团

给出在同一时刻流体微团中任意两点速度之间的关系

分析流体微团的运动形式

流体微团运动时，不像刚体那么简单，除了可以平动和转动外，还伴随有变形运动。变形运动可分为体变形和角变形两种。

（1）平动

所谓平动运动，是一个流体微团移动到另一个地方，微团内各质点的相对位置没有发生变化，微团的形状也没有发生变化，也称平移。

（2）旋转

流体微团的转动和刚体的转动不同，如果在流体微团中引出若干条直线，它们的旋转角速度可以各不相同。因此，要说流体微团的旋转，只能是平均。

 可见，在一般情况下，流体微团的运动总是可以分解成：整体平移运动、旋转运动、线变形运动及角变形运动，与此相对应的是平移速度、旋转角速度、线变形速率和剪切（角）变形速率。

有旋流动和无旋流动

流体微团的角速度矢量：

依据场论的表示法：

涡量：

涡通量：涡量在一截面上的面积分

速度环量：速度矢量沿封闭曲线的线积分

   速度环量的正负不仅与速度方向有关，而且与积分时所取的绕行方向有关。通常规定逆时针方向为K的正方向，即封闭曲线所包围的面积总在前进方向的左侧。

    由此可见，在流体流动中，如果涡量的三个分量中有一个不等于零，即为有旋流动。如果在一个流动区域内各处的涡量或它的分量都等于零，也就是沿任何封闭曲线的速度环量都等于零，则在这个区域内的流动一定是无旋流动。

 上理考研周导师的哔哩哔哩频道

我在上面讲课哦

资料仅供学习使用

如有错误欢迎留言交流

上理考研周导师的其他专栏：

光电融合集成电路技术     电路原理

C语言       复变函数与积分变换

单片机原理

模式识别原理

数字电子技术

自动控制原理 ​​​​​​    ​​​​​​ 传感器技术

模拟电子技术

数据结构

 概率论与数理统计

高等数学

传感器检测技术

智能控制

嵌入式系统

图像处理与机器视觉

热工与工程流体力学

数字信号处理

线性代数

工程测试技术

大学物理

上理考研周导师了解更多