大家好,欢迎来到IT知识分享网。
2-sat基础
2-sat简介
2-SAT,简单的说就是给出 n n n 个集合,每个集合有两个元素,已知若干个 < a , b > <a,b> <a,b>,表示 a a a 与 b b b 矛盾(其中 a a a 与 b b b 属于不同的集合)。然后从每个集合选择一个元素,判断能否一共选 n n n 个两两不矛盾的元素。显然可能有多种选择方案,一般题中只需要求出一种即可。
比如邀请人来吃喜酒,夫妻二人必须去一个,然而某些夫妻之间有矛盾,那么我们要确定能否避免来人之间有矛盾,有时需要方案。这是一类生活中常见的问题。
算法原理
参考网上公认的大牛的文章,提供两种不同的思考方向
- 由对称性解2-SAT问题
- 2-SAT 解法浅析
通用解题思路
假设有 a 1 , a 2 a1,a2 a1,a2 ,和 b 1 , b 2 b1,b2 b1,b2 两对元素, < a 1 , b 1 > <a1,b1> <a1,b1> 表示 a 1 , b 1 a1,b1 a1,b1 之间有矛盾,由于 a a a 和 b b b 必须选出一个,我们用两条有向边 ( a 1 , b 2 ) (a1,b2) (a1,b2) ( b 1 , a 2 ) (b1,a2) (b1,a2) 表示下面两个方案
- 选择 a 1 a1 a1 ,由于 < a 1 , b 1 > <a1,b1> <a1,b1> ,那么必须选择 b 2 b2 b2
- 选择 b 1 b1 b1 ,由于 < a 1 , b 1 > <a1,b1> <a1,b1> ,必须选择 a 2 a2 a2
类似的构造完所有边之后,我们跑一遍 T a r j a n Tarjan Tarjan 判断是否有一个集合中的两个元素在同一个 S C C SCC SCC 中,若有则输出不可能,否则输出方案。构造方案只需要把几个不矛盾的 S C C SCC SCC 拼起来就好了。
输出方案时可以通过变量在图中的拓扑序确定该变量的取值。如果变量 x x x 的拓扑序在 ¬ x \neg x ¬x 之后,那么取 x x x 值为真。应用到 T a r j a n Tarjan Tarjan 算法的缩点,即 x x x 所在 S C C SCC SCC 编号在 ¬ x \neg x ¬x 之前时,取 x x x 为真,否则取 x x x 为假。因为 T a r j a n Tarjan Tarjan 算法求强连通分量时使用了栈,所以 T a r j a n Tarjan Tarjan 求得的 S C C SCC SCC 编号相当于反拓扑序。
时间复杂度为 O ( n + m ) O(n+m) O(n+m)
加深理解
【模板】2-SAT 问题
题目描述
有 n n n 个布尔变量 x 1 x_1 x1 ∼ \sim ∼ x n x_n xn,另有 m m m 个需要满足的条件,每个条件的形式都是 「 x i x_i xi 为 true / false 或 x j x_j xj 为 true / false」。比如 「 x 1 x_1 x1 为真或 x 3 x_3 x3 为假」、「 x 7 x_7 x7 为假或 x 2 x_2 x2 为假」。
2-SAT 问题的目标是给每个变量赋值使得所有条件得到满足。
输入格式
第一行两个整数 n n n 和 m m m,意义如题面所述。
接下来 m m m 行每行 4 4 4 个整数 i i i, a a a, j j j, b b b,表示 「 x i x_i xi 为 a a a 或 x j x_j xj 为 b b b」( a , b ∈ { 0 , 1 } a, b\in \{0,1\} a,b∈{
0,1})
输出格式
如无解,输出 IMPOSSIBLE;否则输出 POSSIBLE。
下一行 n n n 个整数 x 1 ∼ x n x_1\sim x_n x1∼xn( x i ∈ { 0 , 1 } x_i\in\{0,1\} xi∈{
0,1}),表示构造出的解。
数据范围
1 ≤ n , m ≤ 1 0 6 1≤n,m≤10^6 1≤n,m≤106
求解思路
每一个条件都是形如 a ∨ b a\lor b a∨b 的约束,各种约束条件对应的逻辑命题如下:
| a ∨ b a \lor b a∨b | ¬ a → b \neg a \to b ¬a→b ¬ b → a \neg b \to a ¬b→a |
|---|---|
| ¬ a ∨ b \neg a \lor b ¬a∨b | a → b a \to b a→b ¬ b → ¬ a \neg b \to \neg a ¬b→¬a |
| a ∨ b a\lor b a∨b | ¬ a → ¬ b \neg a \to \neg b ¬a→¬b b → a b \to a b→a |
| ¬ a ∨ ¬ b \neg a\lor \neg b ¬a∨¬b | a → ¬ b a \to \neg b a→¬b b → ¬ a b \to \neg a b→¬a |
建图之后判断是否存在 x x x和 ¬ x \neg x ¬x在同一强连通分量,若不存在则有解,否则无解。
如果 x x x的拓扑序 在 ¬ x \neg x ¬x 之后,选择 x x x ,否则选择 ¬ x \neg x ¬x ,实际处理的时候, t a r j a n tarjan tarjan 求得的是反拓扑序,即 x x x 和 ¬ x \neg x ¬x 谁序号越小选谁。
代码
#include <bits/stdc++.h> using namespace std; const int N = 4e6+7,M=2*N; int a[N]; int h[N],e[M],ne[M],idx=1; bool st[N]; int d[N],pre[N]; void add(int a,int b) {
e[idx]=b; ne[idx]=h[a]; h[a]=idx++; } int n,m; int dfn[N],low[N],times=0; stack<int>stk; bool in_stk[N]; int scc[N],sid=0; void tarjan(int u) {
low[u]= dfn[u]= ++times; stk.push(u); in_stk[u]=true; for(int i=h[u];i;i=ne[i]){
int j=e[i]; if(!dfn[j]){
tarjan(j); low[u]=min(low[j],low[u]); }else if(in_stk[j]){
low[u]=min(low[j],low[u]); } } if(low[u]==dfn[u]){
int p; ++sid; do{
p=stk.top(); stk.pop(); in_stk[p]=false; scc[p]=sid; }while(p!=u); } } bool solve() {
for(int i=1;i<=2*n;i++) if(!dfn[i]) tarjan(i); for(int i=1;i<=n;i++){
if(low[i]==low[i+n]) return false; } return true; } int main() {
cin>>n>>m; int x,a,y,b; while(m--){
cin>>x>>a>>y>>b; if(a==1&&b==1){
add(x+n,y); add(y+n,x); }else if(a==1&&b==0){
add(x+n,y+n); add(y,x); }else if(a==0&&b==1){
add(x,y); add(y+n,x+n); }else if(a==0&&b==0){
add(x,y+n); add(y,x+n); } } if(solve()){
cout<<"POSSIBLE"<<endl; for(int i=1;i<=n;i++){
cout<<(scc[i]<scc[i+n])<<' '; } }else cout<<"IMPOSSIBLE"<<endl; return 0; } 卡图难题
题目描述
有 n n n 个布尔变量 X 0 X_0 X0 ∼ \sim ∼ X n − 1 X_n-1 Xn−1,每个变量的可能取值为 0 0 0或 1 1 1。
给定M个算式,每个算是形如 X a X_a Xa o p op op X b = c X_b = c Xb=c ,其中 a a a , b b b 是变量编号, c c c 是数字 0 0 0或 1 1 1, o p op op 是 A N D AND AND O R OR OR X O R XOR XOR三个位运算之一。
求是否存在对每个变量的合法赋值,使所有算式都成立。
输入格式
第一行两个整数 n n n 和 m m m。
接下来 M M M行,每行包含三个整数 a , b , c a,b,c a,b,c,以及一个位运算( A N D AND AND, O R OR OR, X O R XOR XOR 中的一个)。
输出格式
输出结果,如果存在,输出 YES,否则输出 NO。
数据范围
1 < = N < = 1000 1<=N<=1000 1<=N<=1000
1 < = M < = 1 0 6 1<=M<=10^6 1<=M<=106
输入样例
4 4 0 1 1 AND 1 2 1 OR 3 2 0 AND 3 0 0 XOR 输出样例
YES 求解思路
每个元素都只有两种取值方案,这仍然是一道2-sat
同样按题目要求得出对应的逻辑,按照一下逻辑构图,
| a & b = 1 a \& b =1 a&b=1 | ¬ a → a \neg a \to a ¬a→a ¬ b → b \neg b \to b ¬b→b |
|---|---|
| a & b = 0 a \& b =0 a&b=0 | a → ¬ b a \to \neg b a→¬b b → ¬ a b \to \neg a b→¬a |
| a ∣ b = 1 a|b=1 a∣b=1 | ¬ a → b \neg a \to b ¬a→b ¬ b → a \neg b \to a ¬b→a |
| a ∣ b = 0 a|b=0 a∣b=0 | a → ¬ a a \to \neg a a→¬a b → ¬ b b \to \neg b b→¬b |
| a ∧ b = 1 a \land b=1 a∧b=1 | a → b a \to b a→b b → a b \to a b→a ¬ a → ¬ b \neg a \to \neg b ¬a→¬b ¬ b → ¬ a \neg b \to \neg a ¬b→¬a |
| a ∧ b = 0 a \land b=0 a∧b=0 | a → ¬ b a \to \neg b a→¬b b → ¬ a b \to \neg a b→¬a ¬ a → b \neg a \to b ¬a→b ¬ b → a \neg b \to a ¬b→a |
我们用 x x x表示 1 1 1, x + n x+n x+n 表示0 也就是 ¬ x \neg x ¬x
建图之后判断是否存在 x x x和 ¬ x \neg x ¬x在同一强连通分量,若不存在则有解,否则无解。
//tarjan直接套用即可 bool solve() {
for(int i=0;i<2*n;i++) if(!dfn[i]) tarjan(i); for(int i=0;i<n;i++){
if(low[i]==low[i+n]) return false; } return true; } int main() {
cin>>n>>m; int a,b,c; string ch; while(m--){
cin>>a>>b>>c>>ch; if(ch[0]=='A'){
if(c==1) {
add(a+n,a);add(b+n,b); } else {
add(a,b+n);add(b,a+n); } }else if(ch[0]=='O'){
if(c==1){
add(a+n,b);add(b+n,a); }else {
add(a,a+n);add(b,b+n); } }else {
if(c==1) {
add(a,b);add(b,a); add(a+n,b+n);add(b+n,a+n); }else {
add(a,b+n);add(a+n,b); add(b,a+n);add(b+n,a); } } } if(solve()) cout<<"YES"<<endl; else cout<<"NO"<<endl; return 0; } Wedding
题目描述
最多30对新人将参加婚宴,他们将坐在长桌的两边。新娘和新郎坐在一端,彼此相对,新娘戴着一个精心制作的头饰,她不会看到和她坐在同一边的人。丈夫和妻子坐在桌子的同一侧被认为是不吉利。此外,还有几对人存在矛盾,有矛盾的人坐在同一侧也被认为是不吉利的。你的工作是安排餐桌上的人,以避免任何不吉利
输入格式
输入包含多组测试用例。
第一行两个整数 n n n 和 m m m。表示共有 n n n 对夫妇, m m m 对矛盾关系。接下来 m m m 行,每行揭露一个矛盾关系。
如 7h 3w 表示第 7 对夫妇中的丈夫和第 3 对夫妇中的妻子有矛盾。
每对夫妇被编号为 0,1,...,n-1,其中新郎新娘的编号为 0。
当输入一行为 0 0 时,表示输入终止。
输出格式
每组测试用例输出一个结果,每个结果占一行。结果包含同新娘坐在一侧的人员列表。如果有多种方案,随便输出一种即可。
输出结果时,请按照编号从小到大的顺序,输出人员。如果没有方案,则输出 bad luck。
输入样例
10 6 3h 7h 5w 3w 7h 6w 8w 3w 7h 3w 2w 5h 0 0 输出样例
1h 2h 3w 4h 5h 6h 7h 8h 9h 求解思路
1.首先定义i为妻子,i+n为丈夫,夫妻之中妻子的真值为true,丈夫的真值为false(可以尝试换一种定义方式,然后修改代码,检验自己是否完全理解 2 − s a t 2-sat 2−sat)
2.题目要求输出和新娘在同一侧的人员名单,而新娘的编号是0,也就是说在有解的情况下,0是必选的,0与n是夫妻关系,n必不选,为了必选0,需要加一条由丈夫指向妻子的边,即add(n,0)
3.如果有解,那么选择夫妻之间拓扑序小的坐新娘这侧。
代码
//tarjan模板略 void init() {
memset(h, 0, sizeof h); memset(dfn, 0, sizeof dfn); memset(low, 0, sizeof low); memset(in_stk, 0, sizeof in_stk); memset(scc, 0, sizeof scc); while (!stk.empty()) stk.pop(); idx = 1; sid = 0; } int main() {
int cnt=0; while (cin >> n >> m) {
if (n + m == 0) break; init(); int a,c,pa,pc; char b,d; while(m--){
cin>>a>>b>>c>>d; if(b=='h') pa=a,a=a+n; else pa=a+n; if(d=='h') pc=c,c=c+n; else pc=c+n; add(pa,c); add(pc,a); } add(n,0); if (solve()) {
for (int i = 1; i < n; i++) {
if (scc[i] < scc[i + n]) cout << i << 'w' << ' '; else cout << i << 'h' << ' '; } } else {
cout << "bad luck"; } cout << endl; } return 0; } 平面图判定
题目描述
若能将无向图 G = ( V , E ) G=(V, E) G=(V,E) 画在平面上使得任意两条无重合顶点的边不相交,则称 G G G 是平面图。判定一个图是否为平面图的问题是图论中的一个重要问题。现在假设你要判定的是一类特殊的图,图中存在一个包含所有顶点的环,即存在哈密顿回路。
输入格式
输入文件的第一行是一个正整数 T T T,表示数据组数 (每组数据描述一个需要判定的图)。
每组数据的第一行是用空格隔开的两个正整数 N N N 和 M M M,分别表示对应图的顶点数和边数。
紧接着 M M M 行,每行两个正整数 u u u 和 v v v ( 1 ≤ u , v ≤ N ) \left(1\leq u,v\leq N\right) (1≤u,v≤N),表示对应图的一条边 ( u , v ) \left(u,v\right) (u,v), 输入的数据保证所有边仅出现一次。
每组数据的最后一行是用空格隔开的 N N N 个正整数,从左到右表示对应图中的一个哈密顿回路: V 1 , V 2 , … , V N V_1,V_2,…,V_N V1,V2,…,VN,即对任意 i ≠ j i\not=j i=j 有 V i ≠ V j V_i\not=V_j Vi=Vj 且对任意 1 ≤ i ≤ N − 1 1\leq i\leq N-1 1≤i≤N−1 有 ( V i , V i − 1 ) ∈ E \left(V_i,V_i-1\right)\in E (Vi,Vi−1)∈E 及 ( V 1 , V N ) ∈ E \left(V_1,V_N\right)\in E (V1,VN)∈E。输入的数据保证 100 % 100\% 100% 的数据满足 T ≤ 100 , 3 ≤ N ≤ 200 , M ≤ 10000 T\leq100,3\leq N\leq200,M\leq10000 T≤100,3≤N≤200,M≤10000。
输出格式
包含 T T T 行,若输入文件的第 i i i 组数据所对应图是平面图,则在第 i i i 行输出 YES \text{YES} YES,否则在第 i i i 行输出 NO \text{NO} NO,注意均为大写字母
输入样例
2 6 9 1 4 1 5 1 6 2 4 2 5 2 6 3 4 3 5 3 6 1 4 2 5 3 6 5 5 1 2 2 3 3 4 4 5 5 1 1 2 3 4 5 输出样例
NO YES 解题思路
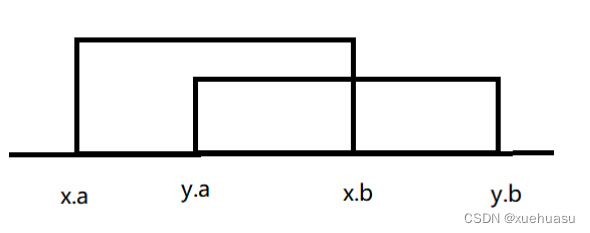
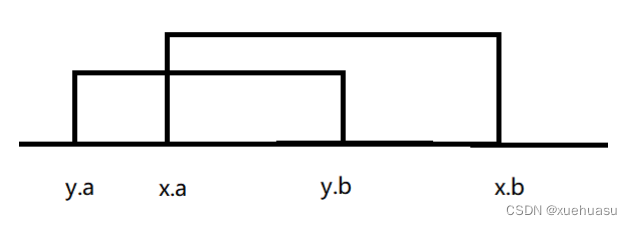
假设黑线是哈密顿环的一部分,红线是除了环之外的其他边,假设所有的边都在环的内部(上图),如果发现两条边相交,我们一定可以把其中一条边画在环的外部从而避免相交(下图),于是我们的 2 − s a t 2-sat 2−sat模型就是所有两两相交的边,不能同时出现在内部或者外部(如果在内部相交,那么在外部也一定会相交)。
接下来要思考的是如何判断两条边必相交,其实只要按照哈密顿环上点的顺序给 V V V 编号,然后判断两条边是否有交叉区域即可。
如上图,相交一共两种情况,注意构成哈密顿环的边是不参与比较的。
现在给出此题的 2 − s a t 2-sat 2−sat 模型,定义: x x x 为在环内的边, ¬ x \neg x ¬x 在环外的边,对于不属于哈密顿环的不同的两条边 a , b a,b a,b,如果相交,则有如下关系:
a → ¬ b , ¬ a → b , b → ¬ a , ¬ b → a a \to \neg b,\neg a \to b, b \to \neg a ,\neg b \to a a→¬b,¬a→b,b→¬a,¬b→a
最后还有一个平面图的性质: m < = 3 n − 6 m<=3n-6 m<=3n−6
代码
#include <iostream> #include <algorithm> #include <string.h> #include <queue> #include <set> #include <map> using namespace std; #define ll long long const int N = 1e5+7,M=N,V=510; #define x first #define y second int h[N],e[M],ne[M],idx=1; void add(int a,int b) {
e[idx]=b; ne[idx]=h[a]; h[a]=idx++; } typedef pair<int,int>PII; PII edge[N]; int hmd[V]; bool is_hmd[V][V]; int n,m; int dfn[N],low[N],times; int stk[N],top; bool in_stk[N]; int scc[N],sid; void tarjan(int u) {
low[u]= dfn[u]= ++times; stk[++top]=u; in_stk[u]=true; for(int i=h[u];i;i=ne[i]){
int j=e[i]; if(!dfn[j]){
tarjan(j); low[u]=min(low[j],low[u]); }else if(in_stk[j]){
low[u]=min(dfn[j],low[u]); } } if(low[u]==dfn[u]){
int p; ++sid; do{
p=stk[top--]; in_stk[p]=false; scc[p]=sid; }while(p!=u); } } bool check(int i,int j)//相交返回true {
int ax=hmd[edge[i].x],ay=hmd[edge[i].y]; int bx=hmd[edge[j].x],by=hmd[edge[j].y]; if(bx > ax && bx < ay && by > ay) return true; if(by > ax && by < ay && bx < ax) return true; return false; } bool solve() {
memset(h,0,sizeof h); memset(is_hmd,0,sizeof is_hmd); memset(dfn,0,sizeof dfn); memset(in_stk,0,sizeof stk); idx=1;times=0;top=0;sid=0; scanf("%d %d",&n,&m); int a,b; for(int i=1;i<=m;i++){
scanf("%d %d",&a,&b); edge[i]={
a,b}; } scanf("%d",&a); hmd[a]=1;//存下当前下标是哈密顿路径的第几个点 int first=a; for(int i=2;i<=n;i++){
scanf("%d",&b); hmd[b]=i; is_hmd[a][b]=is_hmd[b][a]=true;//a,b之间的路径是哈密顿路径 a=b; } is_hmd[first][a]=is_hmd[a][first]=true; if(m>3*n-6) return false; int cnt=0; for(int i=1;i<=m;i++){
//要将原图转换2-sat模型,首先排除掉哈密顿环上的边 if(is_hmd[edge[i].x][edge[i].y]) continue; if(hmd[edge[i].x]<hmd[edge[i].y]) edge[++cnt]=edge[i]; else edge[++cnt]={
edge[i].y,edge[i].x}; } m=cnt; for(int i=1;i<=m;i++){
for(int j=i+1;j<=m;j++){
if(check(i,j)) {
//判断边i,j是否相交,在此之前已经保证不存在哈密顿环的边 add(i,j+m); add(i+m,j); add(j,i+m); add(j+m,i); } } } for(int i=1;i<=2*m;i++){
if(!dfn[i]) tarjan(i); } for(int i=1;i<=m;i++){
if(scc[i]==scc[i+m]) return false; } return true; } int main() {
int t;scanf("%d",&t); while(t--) {
if(solve()) printf("YES\n"); else printf("NO\n"); } return 0; } 免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/110315.html