简单记录一下联邦卡尔曼滤波(需要熟悉KF)

大家好，欢迎来到IT知识分享网。

先上理论，然后再一步一步通俗的讲解。

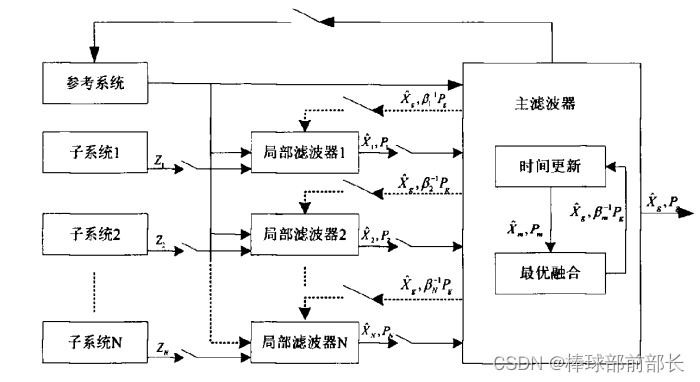
FKF的结构如下图所示，共有两层滤波结构，分别为主滤波器和子滤波器，子滤波器解算出来的最优估计值经过全局融合后，可以获得最终的最优估计值。

假设系统的状态空间模型如下：

$\begin{cases} X_k = \Phi_{k,k-1} X_{k-1} + \Gamma_{k-1} W_{k-1} \\ Z_k = H_k X_k + V_k \end{cases}$

其中， W_k 的协方差矩阵为 Q_k ， V_k 的协方差矩阵为 R_k 。

各个子系统的状态空间模型如下：

$\begin{cases} X_{i,k} = \Phi_{i,(k,k-1)} X_{i,k-1} + \Gamma_{i,k-1} W_{i,k-1} \\ Z_{i,k} = H_{i,k} X_{i,k} + V_{i,k} \end{cases}, \quad i = 1, 2, 3, \ldots$

其中， $W_{i,k}$ 的协方差矩阵为 $Q_{i,k}$ ， V_k 的协方差矩阵为 $R_{i,k}$ 。

那么FKF的解算过程包括以下五个步骤：

1、设置初值：

$P_{i,0} = \beta_i^{-1} P_{g,0}, \quad Q_{i,0} = \beta_i^{-1} Q_{g,0}$

2、预测：

$\hat{X}_{i,k+1/k} = \Phi_{i,k+1/k} \hat{X}_{i,k}\\ P_{i,k+1/k} = \Phi_{i,k+1/k} P_{i,k} \Phi_{i,k+1/k}^T + \Gamma_{i,k} Q_{i,k} \Gamma_{i,k}^T$

3、更新：主滤波器不存在对应的量测信息，所以主滤波器不需要进行量测更新。

$K_{i,k+1} = P_{i,k+1|k} H_{i,k+1}^T \left( H_{i,k+1} P_{i,k+1|k} H_{i,k+1}^T + R_{i,k+1} \right)^{-1} \\\hat{X}_{i,k+1} = \hat{X}_{i,k+1|k} + K_{i,k+1} \left( Z_{i,k+1} - H_{i,k+1} \hat{X}_{i,k+1|k} \right)\\ P_{i,k+1} = \left( I - K_{i,k+1} H_{i,k+1} \right) P_{i,k+1|k}$

4、融合：将子滤波器的局部最优解进行融合，获得融合后的全局最优解。

$P_{g,k} = \left( \sum P_{i,k}^{-1} \right)^{-1} \\\hat{X}_{g,k} = P_{g,k} \sum \left( P_{i,k}^{-1} \hat{X}_{i,k} \right)$

5、信息反馈和分配

$\hat{X}_{i,k} = \hat{X}_{g,k}\\ P_{i,k} = \beta_{i}^{-1} P_{g,k}\\ Q_{i,k} = \beta_{i}^{-1} Q_{g,k}$

通俗的讲：

定义：

$\beta _{m}=0$ （可能用不到）

N=3 （子滤波器的个数）

$\beta _{i}=1/N$ （每个滤波器分配相同的权重）

定义并初始化一个二维位置状态变量 $X=[x_{1},x_{2}]=[0,500]$

定义并初始化系统的状态变量噪声的协方差

定义并初始化系统的状态变量的协方差

定义并初始化三个子系统的观测噪声方差为 $R_{1}=4,R_{2}=1,R_{1}=3$

设每个子滤波器的 $Q_{i}=\frac{1}{\beta _{i}}Q,P_{i}=\frac{1}{\beta _{i}}P$ ，状态转移方程 $F=\begin{bmatrix} cos\theta &-sin\theta \\ sin\theta &cos\theta \end{bmatrix}$ ，观测源位置 $[x_{r},y_{r}]$ 。

系统和各子滤波器的初始位置都是[0,500]，主滤波器和子滤波器的状态转移方程和状态变量都是一致的。

开始子滤波器1的预测步骤：

$\hat{X}_{1,{k|k-1}}=F\hat{X} _{1,k-1}$

$P_{1,k|k-1}=F P_{1,k-1}F ^{T}+Q_{1}$

观测方程 $z_{1}=\sqrt{(x_{1}-x_{r})^{2}+(x_{2}-y_{r})^{2}}$ ，非线性方程需要用EKF，对其求导得 $H_{1}=(\frac{x_{1}-x_{r}}{z_{1}},\frac{x_{2}-y_{r}}{z_{1}})$ ，那么更新步骤为：

$K_{1}=P_{1,k|k-1}H_{1}^{T}(H_{1}P_{1,k|k-1}H_{1}^{T}+R_{1})^{-1}$

$\hat{X}_{1,k}=\hat{X}_{1,k|k-1}+K_{1}(z_{1}-H_{1}\hat{X}_{1,k|k-1})$

$P_{1,k}=((I-K_{1}H_{1})P_{1,k|k-1})^{-1}$

注意这里对状态变量协方差矩阵的更新和传统的相比是取逆的。其它两个子滤波器的更新过程同上。

现在对主滤波器进行预测：

$\hat{X}_{k|k-1}=F\hat{X} _{k-1}\\P_{k|k-1}=(F P_{k-1}F ^{T}+Q)^{-1}$

融合：

$P_{f}=(P_{1,k}+P_{2,k}+P_{3,k}+(P_{k}))\\X_{f}=P_{f}(P_{1,k}X_{1,k}+P_{2,k}X_{2,k}+P_{3,k}X_{3,k}+P_{k}X_{k})$

更新子滤波器和主滤波器的协方差和位置进行下一轮：

$\hat{X} _{1,k-1}=X_{f}\\P_{1,k-1}=\frac{1}\beta_{1} {}P_{f}\\\hat{X} _{2,k-1}=X_{f}\\P_{2,k-1}=\frac{1}\beta_{2} {}P_{f}\\\hat{X} _{3,k-1}=X_{f}\\P_{3,k-1}=\frac{1}\beta_{3} {}P_{f}\\$

用matlab实现这个联邦卡尔曼滤波器：

%% clc clear all; close all; %1.建一个匀速圆周运动的模型 r = 500; x = -r:0.01:r; y = sqrt(r.^2 - x.^2); %运动的轨迹 plot(x,[y;-y],'LineWidth',2); grid on;axis equal;title('质点轨迹','FontSize',16) xlabel('x/m','FontSize',16) ylabel('y/m','FontSize',16) xlim([-2000 2000]) ylim([-2000 2000]) text(750,750,'o','color','g') text(750,750,'雷达1','FontSize',10) text(-750,750,'o','color','g') text(-750,750,'雷达2','FontSize',10) text(0,-1000,'o','color','g') text(0,-1000,'雷达3','FontSize',10) %% %目标的移动 Observation_time = 0.5; v = 10; w = v/r;%角速度 t = 0:Observation_time:2*pi/w;%刚好转一圈 Q = 2;%过程噪声 x_w=sqrt(Q)*randn(1,size(t,2)); y_w=sqrt(Q)*randn(1,size(t,2)); x_traj = r * sin(w*t);%实现刚好走完一圈 y_traj = r * cos(w*t); s_traj = [x_traj;y_traj]; x_ture_traj = r * sin(w*t)+x_w;%实现刚好走完一圈 y_ture_traj = r * cos(w*t)+y_w; ture_traj = [x_ture_traj;y_ture_traj]; %雷达的位置 radar_1 = [750 750]; radar_2 = [-750 750]; radar_3 = [0 -1000]; radar1_noise = 3; radar2_noise = 1; radar3_noise = 4; %真实的测量信号 radar1_ture_measuremnet = sqrt((radar_1(1)-x_ture_traj).^2 + (radar_1(2)-y_ture_traj).^2 ); radar2_ture_measuremnet = sqrt((radar_2(1)-x_ture_traj).^2 + (radar_2(2)-y_ture_traj).^2 ); radar3_ture_measuremnet = sqrt((radar_3(1)-x_ture_traj).^2 + (radar_3(2)-y_ture_traj).^2 ); %加噪声的测量 radar1_noise_measuremnet = radar1_ture_measuremnet + radar1_noise * randn(1,size(radar1_ture_measuremnet,2)); radar2_noise_measuremnet = radar2_ture_measuremnet + radar2_noise * randn(1,size(radar2_ture_measuremnet,2)); radar3_noise_measuremnet = radar3_ture_measuremnet + radar3_noise * randn(1,size(radar3_ture_measuremnet,2)); %% %FR结构的联邦滤波器(融合重置结构) %联邦滤波器 三个子滤波器 一个主滤波器 beta_M = 0; N = 3; beta_i = 1/N;%每个传感器分配的权值是一样的 Q_process_noise_system = diag([2 2]);%系统的过程噪声 P_cov_system = diag([1000 1000 ]);%初始的系统协方差,随便给定的 X_init_state = [0;500];%初始目标的位置 %%%%%%%%%%%%%%%%%%%%%%%%%%%%1.信息分配与重置%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Q_process_noise_radar = 1/(beta_i) * Q_process_noise_system; system_init_pos = X_init_state; object1_init_pos = X_init_state; object2_init_pos = X_init_state; object3_init_pos = X_init_state; object1_correct_pos = X_init_state; object2_correct_pos = X_init_state; object3_correct_pos = X_init_state; fusion_pos = X_init_state; object1_init_cov = 1/(beta_i) * P_cov_system; object2_init_cov = 1/(beta_i) * P_cov_system; object3_init_cov = 1/(beta_i) * P_cov_system; for i = 1:size(radar1_ture_measuremnet,2)-1 %第一个观测值扔掉 %%%%%%%%%%%%%%%%%%%%%%%%%%%%2.传感器时间量测更新%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %由于是匀速圆周运动，所以可以用旋转矩阵来做预测 R = [cos(theta) -sin(theta) ; sin(theta) cos(theta)] %由于旋转矩阵本身的方向是逆时针方向的，而本题物体的运动是顺时针的，所以需要用到旋转矩阵的逆 = 旋转矩阵的转置 theta = w * Observation_time * 1; R = [cos(theta) -sin(theta); sin(theta) cos(theta)]'; %对于每个传感器都是一样的 %% %传感器1 %radar1的卡尔曼子滤波器 %预测 F = R; object1_estimate_pos(:,i+1) = F * object1_init_pos; P_object1_estimate = F * object1_init_cov * F' + Q_process_noise_radar; %更新 %因为观测并不是线性的，所以这里需要用到拓展卡尔曼滤波，对观测方程进行求导 %观测矩阵也是不断变化的，因为是在均值处进行展开 dec = sqrt((radar_1(1)-object1_estimate_pos(1,i+1)).^2 + (radar_1(2)-object1_estimate_pos(2,i+1)).^2); H = [ -(radar_1(1)-object1_estimate_pos(1,i+1))/dec -(radar_1(2)-object1_estimate_pos(2,i+1))/dec]; K = P_object1_estimate * H' * inv(H * P_object1_estimate * H' + radar1_noise) ; object1_correct_pos(:,i+1) = object1_estimate_pos(:,i+1) + K * ( radar1_noise_measuremnet(i+1) - sqrt((radar_1(1)-object1_estimate_pos(1,i+1)).^2 + (radar_1(2)-object1_estimate_pos(2,i+1)).^2)); inform_object1_correct = inv((eye(2) - K * H)*P_object1_estimate); %radar2的卡尔曼子滤波器 object2_estimate_pos(:,i+1) = F * object2_init_pos; P_object2_estimate = F * object2_init_cov * F' + Q_process_noise_radar; %更新 dec = sqrt((radar_2(1)-object2_estimate_pos(1,i+1)).^2 + (radar_2(2)-object2_estimate_pos(2,i+1)).^2); H = [ -(radar_2(1)-object2_estimate_pos(1,i+1))/dec -(radar_2(2)-object2_estimate_pos(2,i+1))/dec]; K = P_object2_estimate * H' * inv(H * P_object2_estimate * H' + radar2_noise) ; object2_correct_pos(:,i+1) = object2_estimate_pos(:,i+1) + K * ( radar2_noise_measuremnet(i+1) - sqrt((radar_2(1)-object2_estimate_pos(1,i+1)).^2 + (radar_2(2)-object2_estimate_pos(2,i+1)).^2)); inform_object2_correct = inv((eye(2) - K * H)*P_object2_estimate); %% %radar3的卡尔曼子滤波器 %object3_init_pos object3_estimate_pos(:,i+1) = F * object3_init_pos; P_object3_estimate = F * object3_init_cov * F' + Q_process_noise_radar; %更新 dec = sqrt((radar_3(1)-object3_estimate_pos(1,i+1)).^2 + (radar_3(2)-object3_estimate_pos(2,i+1)).^2); H = [ -(radar_3(1)-object3_estimate_pos(1,i+1))/dec -(radar_3(2)-object3_estimate_pos(2,i+1))/dec]; K = P_object3_estimate * H' * inv(H * P_object3_estimate * H' + radar3_noise) ; object3_correct_pos(:,i+1) = object3_estimate_pos(:,i+1) + K * ( radar3_noise_measuremnet(i+1) - sqrt( (radar_3(1)-object3_estimate_pos(1,i+1)).^2 + (radar_3(2)-object3_estimate_pos(2,i+1)).^2) ); inform_object3_correct = inv((eye(2) - K * H)*P_object3_estimate); %%%%%%%%%%%%%%%%%%%%%%%%%%%%3.主滤波器时间更新%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %主滤波器 有3种模式，NR,ZR,FS system_estimate_pos = F * system_init_pos; system_estimate_cov = F * P_cov_system * F' + Q_process_noise_system; %%%%%%%%%%%%%%%%%%%%%%%%%%%%4.最后的融合处理%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% fusion_cov = inv( inform_object1_correct + inform_object2_correct + inform_object3_correct + inv(system_estimate_cov)); fusion_pos(:,i+1) = fusion_cov* (inform_object1_correct *object1_correct_pos(:,i+1) + inform_object2_correct * object2_correct_pos(:,i+1) + inform_object3_correct *object3_correct_pos(:,i+1) + inv(system_estimate_cov) * system_estimate_pos ); object1_init_pos = fusion_pos(:,i+1); object1_init_cov = 1/(beta_i) * fusion_cov; object2_init_pos = fusion_pos(:,i+1); object2_init_cov = 1/(beta_i) * fusion_cov; object3_init_pos = fusion_pos(:,i+1); object3_init_cov = 1/(beta_i) * fusion_cov; system_init_pos = fusion_pos(:,i+1); P_cov_system = fusion_cov ; end plot(x,[y;-y],'LineWidth',2); grid on;axis equal;title('质点轨迹','FontSize',16) xlabel('x/m','FontSize',16) ylabel('y/m','FontSize',16) xlim([-2000 2000]) ylim([-2000 2000]) text(750,750,'o','color','g') text(750,750,'雷达1','FontSize',10) text(-750,750,'o','color','g') text(-750,750,'雷达2','FontSize',10) text(0,-1000,'o','color','g') text(0,-1000,'雷达3','FontSize',10) hold on comet(fusion_pos(1,:),fusion_pos(2,:)) for i=1:size(radar1_ture_measuremnet,2)-1 % Err_S(i)=Dist(ture_traj(:,i),s_traj(:,i));%滤波前的误差 Err_FF(i)=Dist(fusion_pos(:,i),ture_traj(:,i));%滤波前的误差 % Err_UKF(i)=RMS(X(:,i),Xukf(:,i));%滤波后的误差 end % mean_S=mean(Err_S); mean_FF=mean(Err_FF); % mean_UKF=mean(Err_UKF); % mean_PF=mean(Err_PF); t=1:size(radar1_ture_measuremnet,2)-1; figure hold on;box on; % plot(t,Err_Obs,'-'); % plot(t,Err_UKF,'--'); % plot(t,Err_S,'-.'); plot(t,Err_FF,'-.'); % legend('滤波前误差',num2str(mean_Observation),'基本滤波后误差','固定增益滤波后误差'); legend(sprintf('FF滤波后误差%.03f',mean_FF)); xlabel('观测时间/s'); ylabel('误差值'); function d=Dist(X1,X2) if length(X2)<=2 d=sqrt((X1(1,1)-X2(1,1))^2+(X1(2,1)-X2(2,1))^2); else % d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(3))^2); end end

主要参考：Changjing-Liu (Changjing Liu) · GitHub

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/113568.html

简单记录一下联邦卡尔曼滤波(需要熟悉KF)

相关推荐

发表回复