IDFT的python实现

大家好，欢迎来到IT知识分享网。

IDFT

$X[k]$：离散频率下标为k时的频率大小

$x[n]$: 离散时域信号序列

$N$: 信号序列的长度，也就是采样的个数

对比我们之前讲过的DFT，两者公式类似，但是注意在DFT中指数带负号，而IDFT中不带

从矩阵的角度看IDFT

DFT的矩阵表示

IDFT的矩阵表示

从IDFT的公式，可以看出，其实IDFT和DFT表示是一样的，只是对象发生了变化。具体来说，有两个变化：

• 由于指数部分不再有符号，$S_k$进行了共轭操作，得到$S_k^{\ast }$
• 输入是频率信息X[k]

Talk is cheap, show me the code

接下来就简单多了，我们将先介绍如何使用scipy中ifft，然后自己动手实现一份ifft

导入必要的包

import numpy as np from scipy.fftpack import fft, ifft import matplotlib.pyplot as plt %matplotlib notebook 

生成信号用于测试

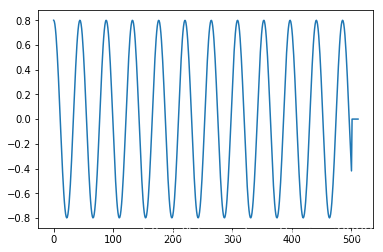
def generate_sine(N, A, fs, f0, phi): ''' N : number of samples A : amplitude fs: sample rate f0: frequency phi: initial phase ''' T = 1/fs n = np.arange(N) x = A*np.cos( 2*np.pi*f0*n*T + phi ) return x # generate signal N = 501 A = 0.8 fs = 44100 f0 = 1000 phi = 0.0 x = generate_sine(N, A, fs, f0, phi) plt.figure() plt.plot(x) plt.show() 

使用scipy中的ifft

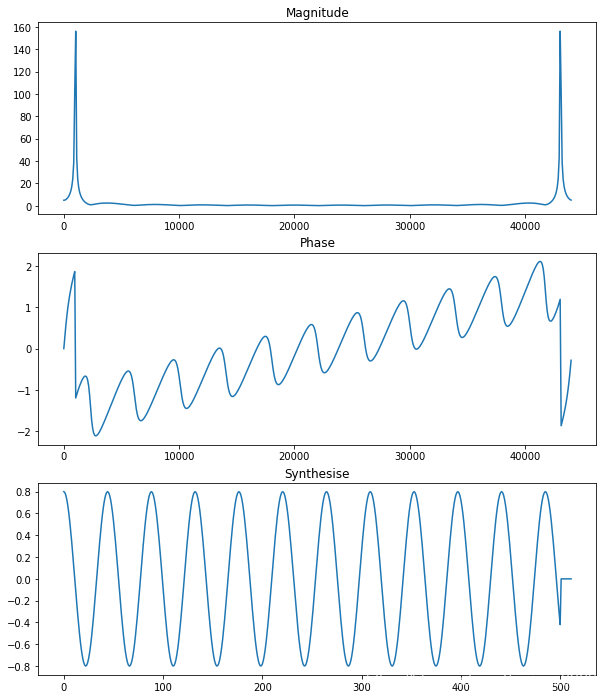
# fft the signal N = 512 # fft size X = fft(x, N) mX = np.abs(X) pX = np.angle(X) freq_axis = np.arange(N)/N * fs plt.figure(figsize=(10, 12)) ax = plt.subplot(3,1,1) plt.plot(freq_axis, mX) ax.set_title('Magnitude') ax = plt.subplot(3,1,2) plt.plot(freq_axis, pX) ax.set_title('Phase') # ifft it ifft_x = ifft(X) ax = plt.subplot(3,1,3) plt.plot(ifft_x) ax.set_title('Synthesise') plt.show() 

自己动手写ifft

只有两个地方要注意：

• 不要忘记乘上 1/N
• $S_k^{\ast }$是$S_k$向量的共轭后的结果。反映在代码中，就是$S_k^{\ast }$不要共轭操作之间返回

def generate_complex_sinusoid(n, N): ''' n : time index (or frequency index) N : number of sample ''' k = np.arange(N) c_sin = np.exp(1j*2*np.pi*k*n/N) return c_sin # ifft loop ifft_x = np.array([]) for i in range(N): s = generate_complex_sinusoid(i, N) ifft_x = np.append(ifft_x, 1/N * np.sum(X*s)) plt.figure() plt.plot(ifft_x) plt.show() 

总结

通过自己动手，我们发现IDFT的原来和实现很简单，几乎与DFT一模一样，唯一需要注意的点就是$S_k^{\ast }$