离散数学——通俗易懂的描述：可图化，可简单图画

大家好，欢迎来到IT知识分享网。

一.基础知识部分

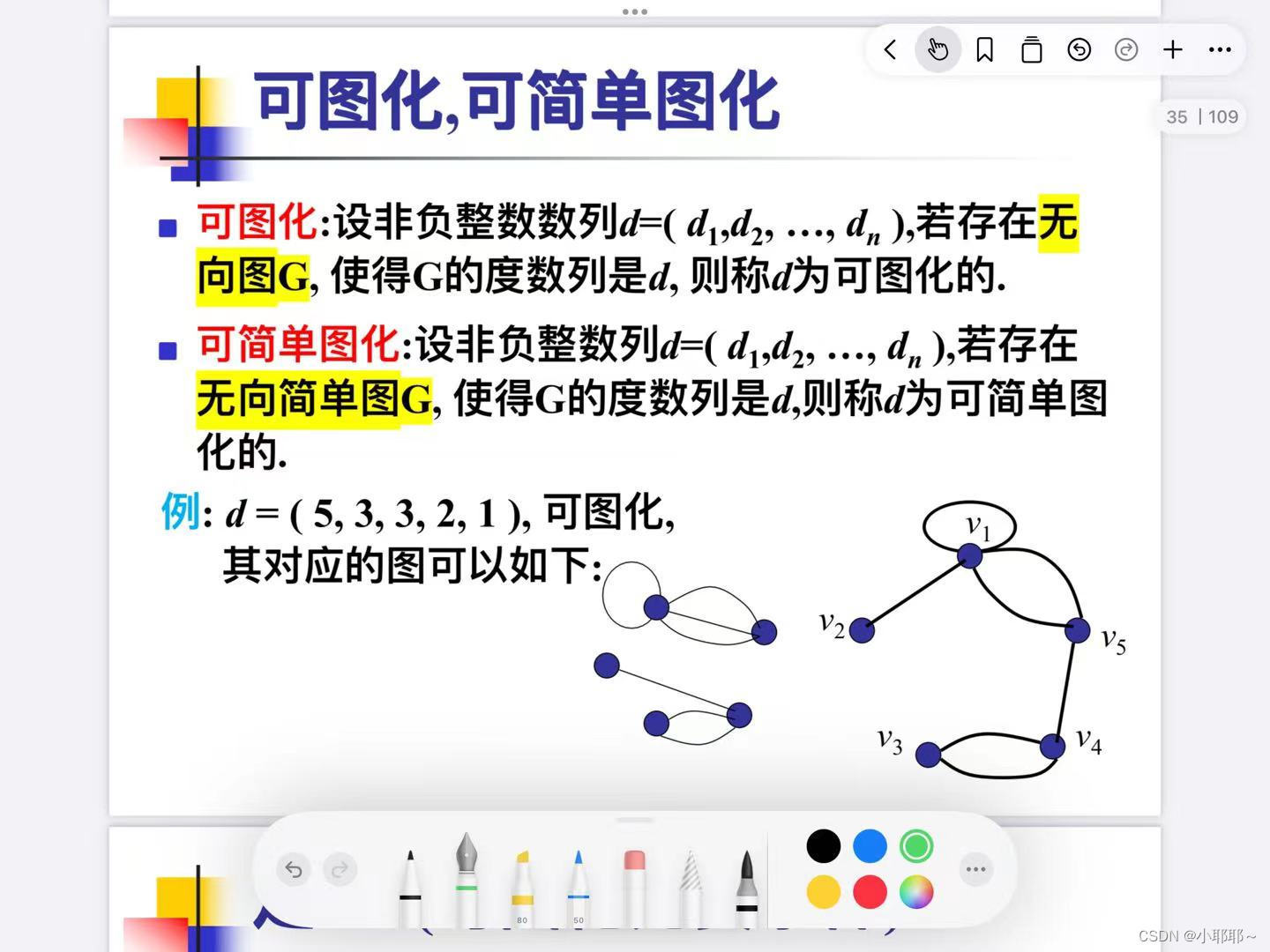
1可图化与可简单图画的定义

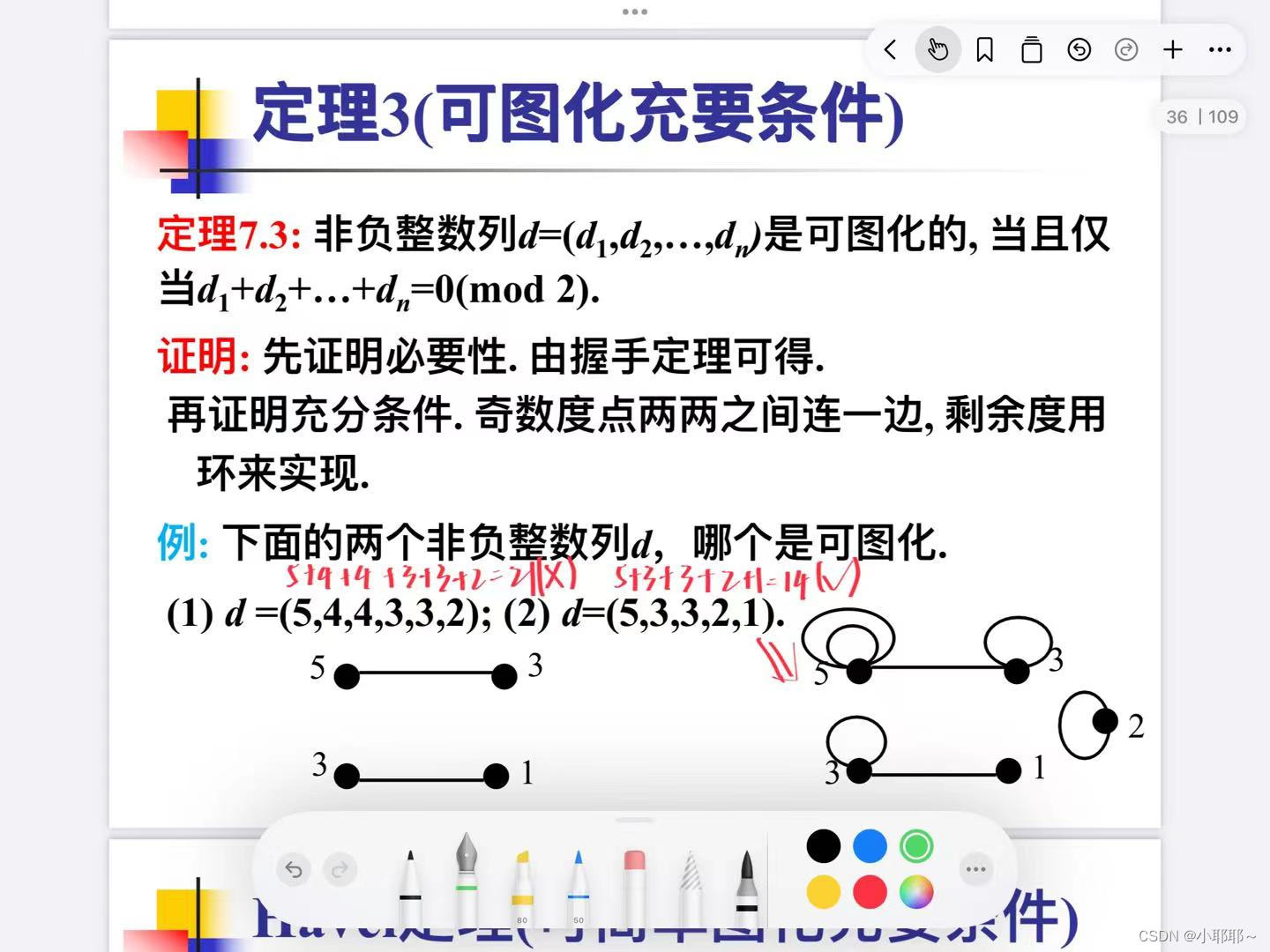
2.判断可图化的充要条件：

其实简单一句话就是：所有度数总和为偶数，就是可图化的，反之也成立

如果还不理解就直接看例子

3.判断可简单图化的充要条件（总共有两种办法：Havel定理和埃尔德什定理）：

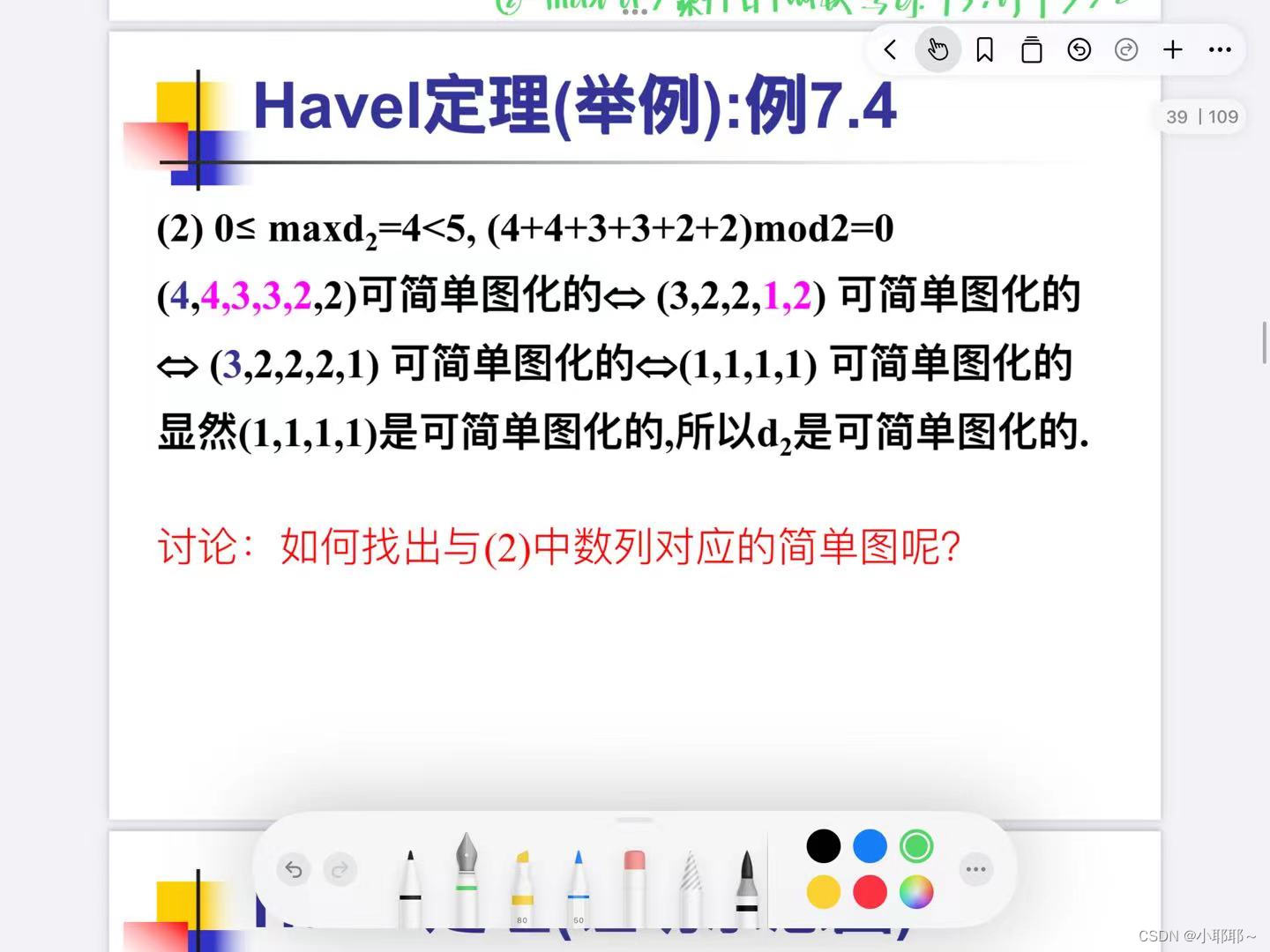
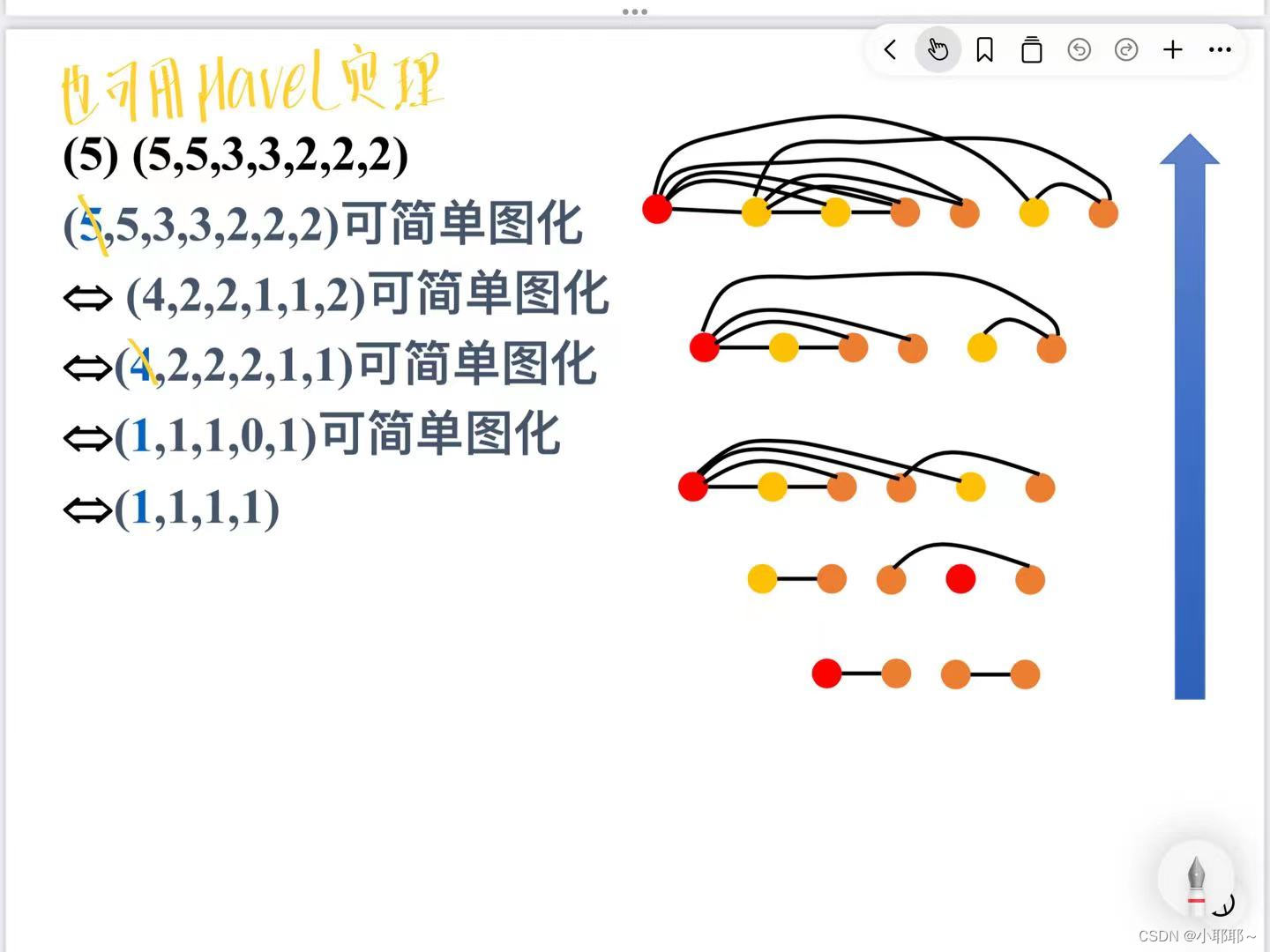
（1）Havel定理

看不懂的话就接看例子理解，然后下一张图片有我总结的步骤，按照步骤会判断就行

接下来是一些例题

步骤：（1）先判断度数之和是否为偶数，即判断是否可图化

           （2）使用Havel定理，即判断是否可简单图化

               注意：使用定理过程中，若出现 1.其中一个点度数为负数  or   2.最大度数>剩下的点数

                          则可判断不可简单图画

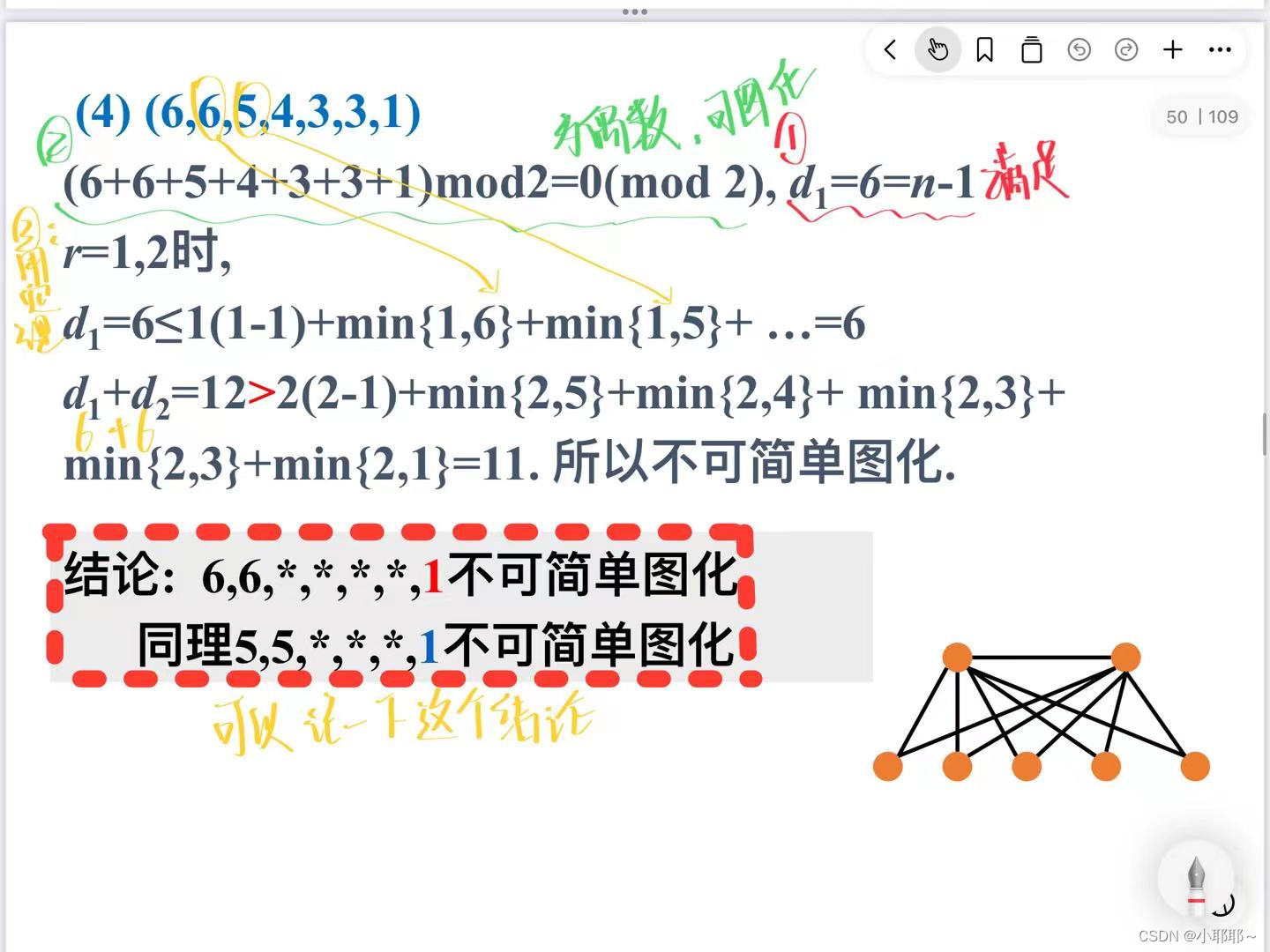
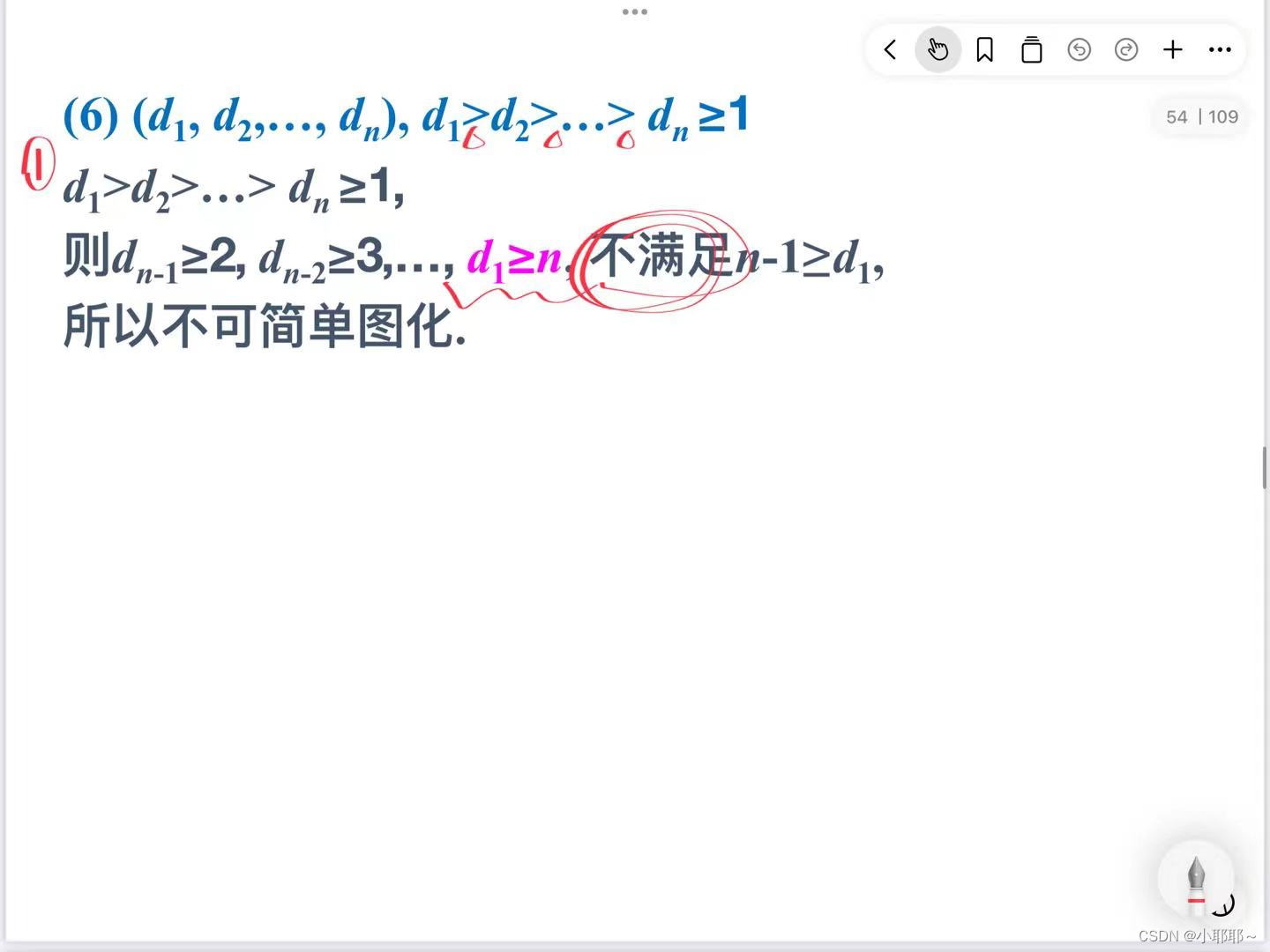
（2）埃尔德什定理

看不懂的话就接看例子理解，然后下一张图片有我总结的步骤，按照步骤会判断就行

接下来是一些例题

步骤：（1）判断 最大度数 小于等于 n-1？

                     判断 最小度数 大于等于 0？

           （2）判断度数之和是否为偶数，即判断是否可图化

           （3）使用埃尔德什定理，即判断是否可简单图化

红色笔是步骤一；绿色笔是第二步；黄色笔是第三步

二.代码实现

1.Havel定理（解析都在注释里面了，只要看懂上面内容就肯定看得懂代码）

bool Havel_Hakimi(int arr[]){ for(int i=0; i<n-1; ++i) { sort(arr+i,arr+n);// 从第i个元素开始进行排序 if(i+arr[i] > n-1) return false;//若第i个元素+arr[i]的值超过n-1，那么不可简单图化 for(int j=i+1; j<=i+arr[i] ; ++j)//如果没有超过n-1，进入循环 { --arr[j]; if(arr[j] < 0) return false; //若出现负数，那么也不可简单化 } } if(arr[n-1]!=0) return false; //若到最后，最小度数不等于0，也不可简单化 return true; 

2.埃尔德什定理(用c语言进行测试，总是判断不对，我就用的python）

def is_graphical(sequence): max_degree = max(sequence) min_degree = min(sequence) total_sum = sum(sequence) n = len(sequence) if max_degree > n - 1 or min_degree < 0 or total_sum % 2 != 0: return False # 不可图化 return True # 可图化 def is_simple_graphical(sequence): sorted_sequence = sorted(sequence, reverse=True) n = len(sorted_sequence) prefix_sum = [0] * n for i in range(n): prefix_sum[i] = prefix_sum[i - 1] + sorted_sequence[i] if sum(sorted_sequence) % 2 != 0: return False # 序列之和为奇数，不可简单图化 while True: if sorted_sequence[0] < 0 or sorted_sequence[0] >= n: return False # 最大度数不在有效范围内，不可简单图化 for i in range(1, sorted_sequence[0] + 1): sorted_sequence[i] -= 1 sorted_sequence[0] = 0 sorted_sequence.sort(reverse=True) count = sum(1 for degree in sorted_sequence if degree == 0) if count == n: return True # 所有度数都为 0，可简单图化 if sorted_sequence[0] < 0: return False # 存在负数，不可简单图化 if __name__ == "__main__": sequence = list(map(int, input("请输入非负整数序列，以空格分隔（例如：2 2 1 1）: ").split())) if not sequence: print("输入错误！") else: if is_graphical(sequence): print("非负整数序列是可图化的。") if is_simple_graphical(sequence): print("非负整数序列是可简单图化的。") else: print("非负整数序列不是可简单图化的。") else: print("非负整数序列不是可图化的。")