转置卷积(transposed-convolution)

大家好，欢迎来到IT知识分享网。

目录

一、什么是转置卷积

1、转置卷积的背景

2、对反卷积的误解

3、转置卷积的计算

二、代码实现

1、padding=0, stride=1和单通道

2、padding≠0, stride≠1和多通道

三、总结

一、什么是转置卷积

1、转置卷积的背景

       通常，对图像进行多次卷积运算后，特征图的尺寸会不断缩小。而对于某些特定任务 (如图像分割和图像生成等)，需将图像恢复到原尺寸再操作。这个将图像由小分辨率映射到大分辨率的尺寸恢复操作，叫做上采样 (Upsample)，如下图所示：

对于上采样(up-sampling)操作，目前有着一些插值方法进行处理：

• 最近邻插值(Nearest neighbor interpolation)
• 双线性插值(Bi-Linear interpolation)
• 双立方插值(Bi-Cubic interpolation) 

       然而，这些上采样方法都是基于人们的先验经验来设计的，在很多场景中效果并不理想 (如：规则固定、不可学习)。因此，我们希望神经网络自己学习如何更好地插值，即接下来要介绍的转置卷积。 与传统的上采样方法相比，转置卷积的上采样方式并非预设的插值方法，而是同标准卷积一样，具有可学习的参数，可通过网络学习来获取最优的上采样方式。

2、对反卷积的误解

       曾经，转置卷积又称反卷积 (Deconvolution)。zfnet在他们可视化的时候，利用到了《Zeiler, M., Taylor, G., and Fergus, R. Adaptive deconvolutional networks for mid and high level featurelearning. In ICCV, 2011》这篇论文中的反卷积操作，进行特征图的可视化，那什么是deconv操作呢？实际上deconv是有误导性的，令人误认为是卷积的逆运算，实际上cnn的卷积是不可逆的，deconv实际上是转置卷积（Transposed Convolution），是对矩阵进行上采样的一种方法。deconv的作用一般有以下几种：

（1）unsupervised learning（无监督学习）：其实就是covolutional sparse coding：这里的deconv只是观念上和传统的conv反向，传统的conv是从图片生成feature map，而deconv是用unsupervised的方法找到一组kernel和feature map，让它们重建图片。
（2）CNN可视化：通过deconv将CNN中conv得到的feature map还原到像素空间，以观察特定的feature map对哪些pattern的图片敏感，这里的deconv其实不是conv的可逆运算，只是conv的transpose，所以tensorflow里一般取名叫transpose_conv。
（3）upsampling（上采样）：在pixel-wise prediction比如image segmentation以及image generation中，由于需要做原始图片尺寸空间的预测，而卷积由于stride往往会降低图片size， 所以往往需要通过upsampling的方法来还原到原始图片尺寸，deconv就充当了一个upsampling的角色。在语义分割中，会在编码器中用卷积层提取特征，然后在解码器中恢复原先尺寸，从而对原图中的每个像素分类。该过程同样需用转置卷积。经典方法有 FCN 和 U-Net。

       反卷积很少用在深度学习中，我们说的反卷积神经网络其实是指用了转置卷积的神经网络。

3、转置卷积的计算

       让我们暂时忽略通道，从基本的转置卷积开始，设步幅为1且没有填充。假设我们有一个的输入张量和一个的卷积核。以步幅为1滑动卷积核窗口，每行次，每列次，共产生个中间结果。每个中间结果都是一个的张量，初始化为0。为了计算每个中间张量，输入张量中的每个元素都要乘以卷积核，从而使所得的张量替换中间张量的一部分。请注意，每个中间张量被替换部分的位置与输入张量中元素的位置相对应。最后，所有中间结果相加以获得最终结果。

       下图解释了如何为的输入张量计算卷积核为的转置卷积。

       一个重要结论：输入高（宽）为、核、填充、步幅，进行转置卷积，如果k=2p+s，那么转置卷积会将输入的高和宽分别放大倍。

二、代码实现

1、padding=0, stride=1和单通道

       我们可以对输入矩阵X和卷积核矩阵K(实现基本的转置卷积运算)trans_conv。

def trans_conv(X, K): # stride=1, padding=0 h, w = K.shape Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1)) for i in range(X.shape[0]): for j in range(X.shape[1]): Y[i: i + h, j: j + w] += X[i, j] * K return Y

       与通过卷积核“减少”输入元素的常规卷积相比，转置卷积通过卷积核“广播”输入元素，从而产生大于输入的输出。我们可以通过构建输入张量X和卷积核张量K从而验证上述实现输出。此实现是基本的二维转置卷积运算。

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]]) K = torch.tensor([[0.0, 1.0], [2.0, 3.0]]) trans_conv(X, K)

tensor([[ 0., 0., 1.], [ 0., 4., 6.], [ 4., 12., 9.]])

       或者，当输入X和卷积核K都是四维张量时，我们可以使用高级API获得相同的结果。

X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2) # (b, c, h, w) tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False) tconv.weight.data = K tconv(X)

tensor([[[[ 0., 0., 1.], [ 0., 4., 6.], [ 4., 12., 9.]]]], grad_fn=<ConvolutionBackward0>)

2、padding≠0, stride≠1和多通道

（1）转置卷积的填充

       与常规卷积不同，在转置卷积中，填充被应用于的输出（常规卷积将填充应用于输入）。例如，当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列。

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False) tconv.weight.data = K tconv(X)

tensor([[[[4.]]]], grad_fn=<SlowConvTranspose2DBackward0>)

（2）转置卷积的步幅

       在转置卷积中，步幅被指定为中间结果（输出），而不是输入。使用fig1中相同输入和卷积核张量，将步幅从1更改为2会增加中间张量的高和权重，如图fig2。

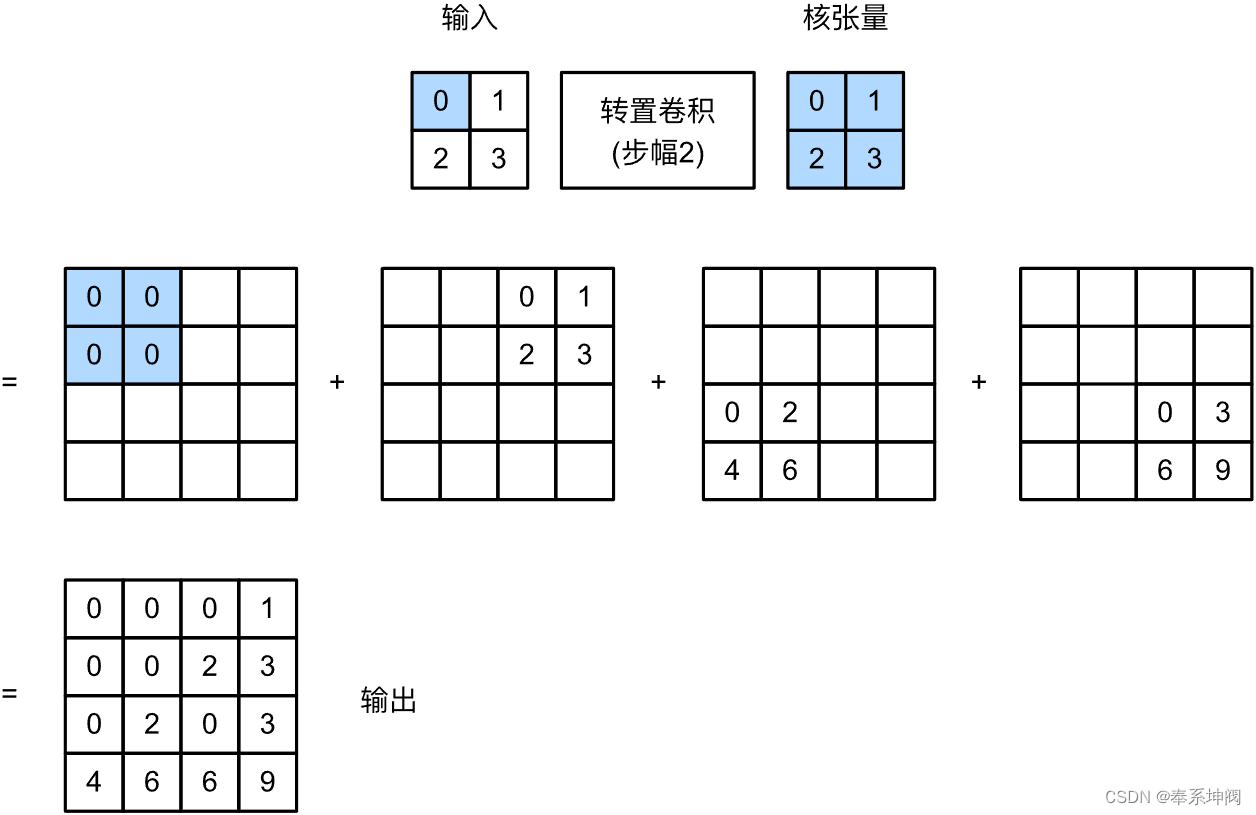
       以下代码可以验证fig2中步幅为2的转置卷积的输出。

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False) tconv.weight.data = K tconv(X)

tensor([[[[0., 0., 0., 1.], [0., 0., 2., 3.], [0., 2., 0., 3.], [4., 6., 6., 9.]]]], grad_fn=<SlowConvTranspose2DBackward0>)

（3）转置卷积中的通道

       对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。假设输入有个通道，且转置卷积为每个输入通道分配了一个的卷积核张量。当指定多个输出通道时，每个输出通道将有一个的卷积核。

       同样，如果我们将代入卷积层来输出，并创建一个与具有相同的超参数、但输出通道数量是中通道数的转置卷积层，那么的形状将与相同。下面的示例可以解释这一点。

X = torch.rand(size=(1, 10, 16, 16)) conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3) tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3) tconv(conv(X)).shape == X.shape

True

三、总结

• 与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出。
• 如果我们将输入卷积层来获得输出并创造一个与有相同的超参数、但输出通道数是中通道数的转置卷积层，那么的形状将与相同。
• 我们可以使用矩阵乘法来实现卷积。转置卷积层能够交换卷积层的正向传播函数和反向传播函数。