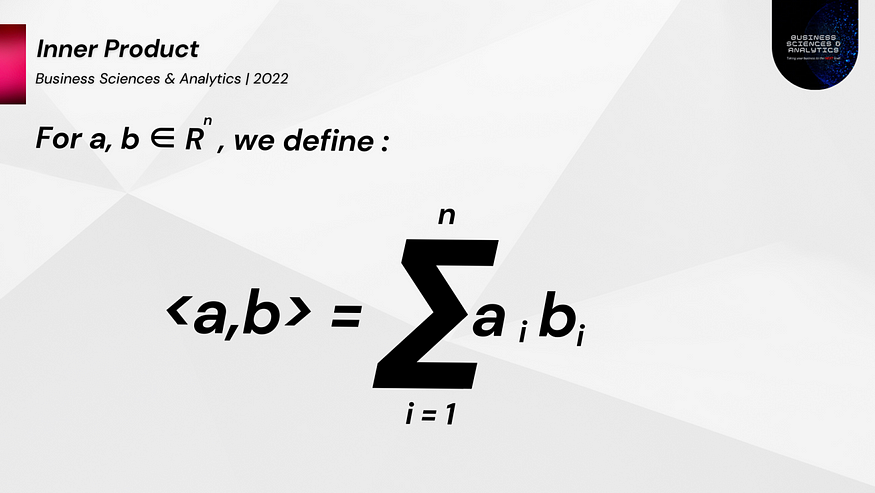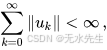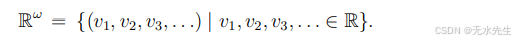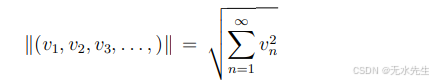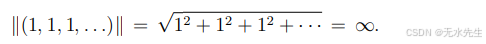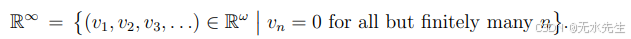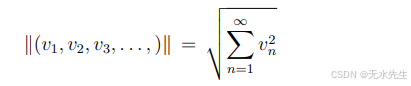大家好,欢迎来到IT知识分享网。
一、说明
在这篇文章中,我们将看看希尔伯特空间,这是一个专门的向量空间,具有超越标准向量空间的独特属性。我们将探讨它的定义特征、基本属性及其在各种数学学科中的深远影响。
在进一步讨论之前,让我们重新审视向量的内积,了解它的定义、性质和意义。
二、什么是内积?
通常表示为 〈 、 〉 或 〈 |〉,内积涉及将 bra 向量与 ket 向量配对,从而产生通常称为“braket”或 Dirac 符号。
狄拉克符号。
它是向量空间固有的一种独特的乘法形式。内积增强了向量空间的结构。内积测量两个向量之间的距离、长度和角度。
标准内积。图片来源:瓦利德·苏拉
三、内积的优点:
F ∈ {R,C}.设 X 是 F 向量空间
- 正定:仅当 x 是 0 向量时,向量 x 与自身的内积应满足 <x,x > ≥ 0,相等 <x,x> = 0
- 共轭对称性 : <x,y> = <y,x > , 仅当 (F(向量空间) ∈ R) 时 , 而是 (F ∈ C) <x,y > = ˉ<y,x >
- 线性度 : <x,y1 + y2> = <x,y1>+ <x,y2>,也<x,λy> = λ<x,y>
3.1 希尔伯特空间 :
希尔伯特空间是一种特殊类型的向量空间,它包含标准向量空间的所有属性,并具有几个附加特征。它的特点是是一个线性向量空间,并具有满足特定条件的内积运算
3.2 希尔伯特空间的优点:
1 — 共轭对称性:“对称内积”,即希尔伯特空间中两个元素的内积是相同内积的复共轭,顺序相反 <Ψ1,Ψ2> = ̄<Ψ2,Ψ1>
此属性可确保当向量的顺序颠倒时,希尔伯特空间中两个向量的内积保持不变,结果是原始内积的复共轭。
注意:复数的复共轭是实部相等和虚部大小相等但符号相反的数。例如,如果 z=a+bi,则 z 的复共轭(表示为 z*)等于 a−bi
2 — 相对于第二个向量的线性度:“线性内积”,此属性断言内积相对于第二个向量是线性的。如果我们取 <Ψ1,aΨ2+bΨ3> 的内积等于 : a <Ψ1,Ψ2> + b <Ψ1,Ψ3>
3 — 非负的确定性:假设我们在 R3 中有一个向量 v=(1,2,3)。那么,v与自身的内积为:〈v,v〉=12+22+32=14。由于这个内积是正的,不等于零,所以v不是零向量,满足正的确定性性质。
4 — 完备性:考虑 R2 中由 Vn =(1/n,1/n) 定义的向量序列。该序列形成柯西序列,因为随着 n 的增加,连续项之间的距离趋近于零。这个序列的极限是零向量 (0, 0),它也在 R2 中,证明了完备性。
如果距离函数如此定义,则任何内积空间都是度量空间,有时也称为豪斯多夫预希尔伯特空间。[6]任何同时也是完全空间的预希尔伯特空间都是希尔伯特空间。[7]
H的完备性可以用H中序列的柯西标准的一种形式来表示:如果每个柯西序列都相对于该范数收敛到空间中的一个元素,则预希尔伯特空间H是完备的。完备性可以用以下等效条件来表征:
如果一系列向量
绝对收敛于
则级数在H中收敛,即部分和收敛于H的一个元素。[8]
作为一个完全赋范空间,希尔伯特空间根据定义也是Banach 空间。因此,它们是拓扑向量空间,其中子集的开放性和封闭性等拓扑概念有明确的定义。特别重要的是希尔伯特空间的闭线性子空间的概念,它通过限制引起的内积也是完全的(是完全度量空间中的闭集),因此本身就是一个希尔伯特空间。
5 — 正交性:设 u=(1,0) 和 v=(0,1) 是 R2 中的向量。那么,“u”和“v”的内积为:<u,v>=1⋅0+0⋅1=0。(由于内积为零,因此 u 和 v 彼此正交。
注意:内积是一种测量两个向量指向同一方向的方法。如果内积为零,则表示向量是垂直的或正交的。
6 — 有界性:有界性是指当算子变换向量时,生成的向量保持在算子本身设定的一定限制内。
四、希尔伯特空间的应用
- 量子力学:描述量子系统的状态,例如粒子的波动函数。
- 信号处理:在平方可积函数空间中分析信号并应用傅里叶分析和小波变换等技术。
- 量子计算:在复杂的希尔伯特空间中将量子比特表示为向量,并通过酉变换操纵它们。
- 图像处理:利用希尔伯特空间执行图像去噪、压缩和特征提取等任务。
- 控制理论:对动态系统进行建模,并使用希尔伯特空间设计控制器来分析系统的稳定性和可控性。
我们已经到了文章的结尾,我们在探索希尔伯特空间的同时探索了向量空间及其性质以及它们的区别,在下一集中见,探索与量子机器学习相关的其他概念
五、附录1:向量空间
向量空间,一组多维量(称为向量)和一组一维量(称为标量),这样向量可以相加,向量可以与标量相乘,同时保留普通的算术性质(结合律、交换律、分配律等)。向量空间是线性代数的基础,并出现在整个数学和物理学中。
向量空间的概念源自普通二维和三维空间的概念,即向量 {u, v, w, …} 的集合以及与之相关的实数域{ a , b , c , …}。意大利数学家首次将向量空间定义为抽象的代数实体1888 年,朱塞佩·皮亚诺 (Giuseppe Peano)提出了向量空间的概念。皮亚诺将他的向量空间称为“线性系统”,因为他正确地看到,可以通过有限多个向量和标量的线性组合(a v + b w + … + c z)得到空间中的任何向量。可以通过这种线性组合生成空间中每个向量的向量集称为生成集。向量空间的维数是最小生成集中向量的数量。(例如,x方向的单位向量与y方向的单位向量与实数组合足以生成二维欧几里得平面中的任意向量。)
六、附录2:范数空间
如果向量空间 V 没有任何有限基,则称向量空间 V 是无限维的。也许无限维向量空间最简单的例子是由所有无限实数序列组成的空间 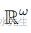
不幸的是,没有明显的方法来对 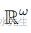
没有定义范数,因为右边的总和可能会有所不同。例如,
如果我们想要一个无限维的赋范空间,我们必须限制为 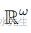
ω。以下示例讨论了这样一个子空间。
对于空间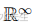
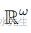
请注意,
此外,函数
一般来说,可能有无穷多个 L 半内积满足此条件。L 半内积是内积的推广,内积是希尔伯特空间与所有其他 Banach 空间的根本区别。这表明所有赋范空间(因此所有 Banach 空间)都可以被视为(预)希尔伯特空间的推广。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/116667.html