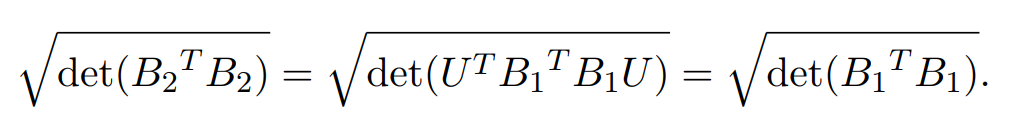格密码的基础概念（1）

大家好，欢迎来到IT知识分享网。

前言

一.格的定义

给定n维空间中一组线性无关向量，其整系数组合构成的集合称为格。

此处的$(b_1,\cdots ,b_n)$定义为格基。同一个格可以由多组不同的格基生成。$b_1,\cdots ,b_n\in$$R^m$,此处如果m=n，则称该“格”满秩。因为格是否满秩对它的性质研究影响不大，所以通常研究满秩的格。
举例：
格基$(1,0{)}^T$与$(0,1{)}^T$可以产生二维空间的所有整数格。如下图：

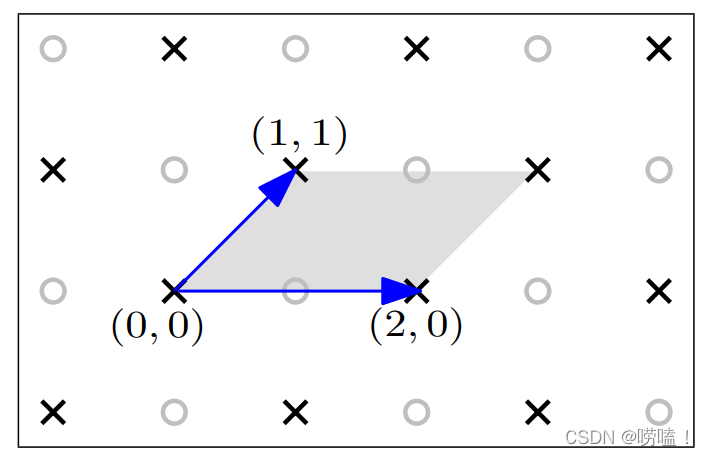
能产生二维空间的所有整数格的格基不唯一，还可以是：$(1,1{)}^T与(2,1{)}^T，(2021,1{)}^T与（1,2022{)}^T$，如下图：

格基$(1,1{)}^T$与$(2,0{)}^T$不能产生二维空间的所有整数格。如下图打“×”的为可产生的格，横纵坐标相加为偶数：

二. 格的延展空间

格基实系数组合生成的空间称为格的延展空间。（区别于前面定义的整数）
s p a n ( L ( B ) ) = s p a n ( B ) = { B a ∣ a ∈ R n } span(L(B))=span(B)=\lbrace Ba|a\in R^n\rbrace span(L(B))=span(B)={
Ba∣a∈Rn}
格的延展空间是整个n维空间的前提：

$$要求为满秩格$$

三. 格的基本区

四.格基的判定定理

秩为n的格$\Lambda$上线性无关的向量组$B=b_1,\cdot \cdot \cdot b_n$为格$\Lambda$的基，当且仅当: P ( B ) ∩ Λ = { 0 } P(B)\cap\Lambda=\lbrace0\rbrace P(B)∩Λ={
0}。
$证明方法$：
（1）证明充分性：当线性无关的向量组$B=b_1,\cdot \cdot \cdot b_n$为格$\Lambda$的基时， P ( B ) ∩ Λ = { 0 } P(B)\cap\Lambda=\lbrace0\rbrace P(B)∩Λ={
0}。
当$b_1,\cdots ,b_n$为$\Lambda$的格基时，格点可以由它们的整数线性组合形成。因为$P(b_1,\cdots ,b_n)$定义为该格基的小于1的小数线性组合，所以很明显二者的交集为空集（或者理解成仅有原点重合）。
充分性证明完毕
（2）证明必要性：当 P ( B ) ∩ Λ = { 0 } P(B)\cap\Lambda=\lbrace0\rbrace P(B)∩Λ={
0}，线性无关的向量组$B=b_1,\cdot \cdot \cdot b_n$为格$\Lambda$的基。
因为$\Lambda$为秩为n的格点，且$b_1,\cdot \cdot \cdot b_n$是线性独立的，可以取$y_i\in R$,使得$x=\sum y_i{b}_i\in \Lambda$，因为格在加减法运算里面是封闭的，所以$x^{\prime }=\sum (y_i-\lfloor y_i\rfloor )b_i$也形成格点。根据条件该格点只能为原点，所以$y_i$必定为整数。
将此过程的推导形成逻辑公式如下：

五. 格基的关系

当给出两组格基$B_1,B_2$，如何判断它们产生的格是一样的呢，也就是$L(B_1)=L(B_2)$吗？
$B_1,B_2$为同一个格的格基，当且仅当存在幺模矩阵U，满足$B_1=B_{2}U$
证明充分性过程如下：
已知$L(B_1)=L(B_2)$，得出$B_2=B_{1}U,U为幺模矩阵$
因为$L(B_1)=L(B_2)$，所以$B_2$中的每一列$b_i$都有，$b_i\in L(B_1)$,这表明必定存在一个整数矩阵$U\in Z^{n\times n}$，使得$B_2=B_{1}U$。同理，也存在$V\in Z^{n\times n}$，使得$B_1=B_{2}V$。
所以可得：
$$B_2=B_{1}U=B_{2}VU$$
将其转置，得到：
$$B_2^T=(VU{)}^T{B}_2^T$$
两式相乘：
$$B_2^T{B}_2=(VU{)}^T{B}_2^T(VU)$$
转置矩阵和原矩阵行列式相等，可得：
$$B_2^T{B}_2=(det(UV){)}^{2}det(B_2^T{B}_2)$$
矩阵相乘再求行列式，和分别求行列式再相乘，结果是一样的，所以：
$$det(V)det(U)=\pm 1$$
因为U和V均为整数矩阵，所以可得：
$$det(U)=det(V)=\pm 1$$
将上述推导过程形成一起，如下:

证明必要性过程如下：
已知$B_2=B_{1}U,U为幺模矩阵$，得出$L(B_1)=L(B_2)$
依据$B_2=B_{1}U$，所以$B_2$的每一列都包含在$L(B_1)$中，所以$L(B_1)$$\subseteq$L$(B_2)$。依据幺模矩阵的性质，$B_1=B_2{U}^{-1}，$同理可得$L(B_2)$$\subseteq$L$(B_1)$。所以$L(B_1)=L(B_2)$。
$提示：行列式等于\pm 1的方阵称为幺模矩阵，幺模矩阵的逆依旧为幺模矩阵。$
$如果学过群环域的知识的话，幺模矩阵在乘法运算下，形成群的概念。$
$此处矩阵乘法的相关性质略。$
推论1：矩阵B是$Z^n$的格基，当且仅当它为幺模矩阵。
推论2：若属于同一个格，则两组基可以相互整系数表示

六. 格基的变换

$B_1,B_2$为同一个格的基，当且仅当可以通过下述变换进行转换：

根据行列式的性质，上式中的变换对应的变换矩阵的行列式为$\pm 1$

七. 格的行列式

格$\Lambda =L(B)$的行列式定义为$det(\Lambda )=\sqrt[2]{det(B^{T}B)}$。
当$\Lambda$满秩时，矩阵B为方阵，格$\Lambda =L(B)$的行列式直接为为$det(\Lambda )=|det(B)|$。
$推论1$：格的行列式与具体基无关。证明如下：
假定$B_1与B_2$为格$\Lambda$的两组不同格基，依据定义六$B_2=B_{1}U,U为幺模矩阵$。可得如下变换：

$推论2$：格行列式的大小与格点的密度成反比。在格的延展空间中取一个n维的球K，球内格点数与$\frac{vol(K)}{det(\Lambda )}$成正比例，其中vol(K)为n维球K的体积。
$推论3$：格的行列式等于格的基本区面积，与具体基无关

八. Gram-Schmidt正交化

如果m=n，该矩阵将为一个正上三角矩阵。

结论

本文可解决的问题：

1. 同一个格可以有多少组不同的基？
2. 格的延展空间总是整个n维空间吗？
3. 在同一个格中，不同格基生成的基本区相同吗？不同的基本区之间有什么关系？
4. 如何判断B是否为格$\Lambda$的基？
5. 根据格的定义，若属于同一个格，则两组基有什么关系？
6. 根据行列式的性质，格基在变换时，对应的变化矩阵需要满足什么条件？
7. 格的行列式等于格基本区的面积，与具体基的选择有关系吗？