数据结构——二叉树的遍历【前序、中序、后序】

大家好，欢迎来到IT知识分享网。

💞💞 前言

hello hello~ ，这里是大耳朵土土垚~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹

💥个人主页：大耳朵土土垚的博客
💥 所属专栏：数据结构学习笔记 、C语言系列函数实现
💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~ 有问题可以写在评论区或者私信我哦~

复习巩固：🥳🥳

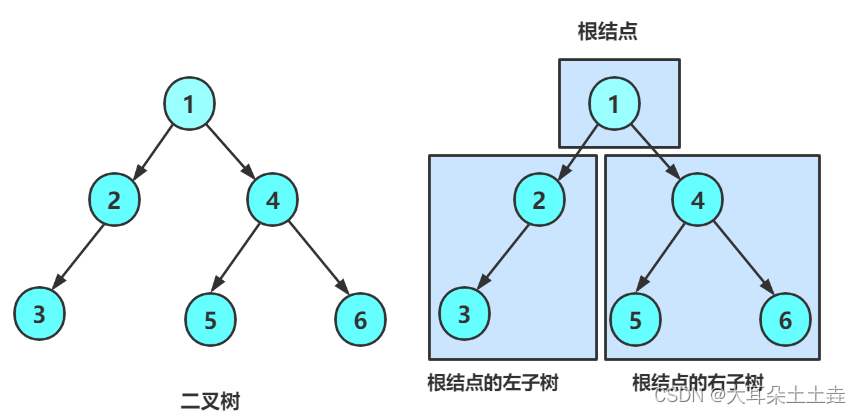
在学习二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的。
   
   从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
   
   

一、手动创建一个简单二叉树🥳🥳

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

手动创建简单二叉树代码如下：

typedef struct BinaryTreeNode { 
    BTDataType data; struct BinaryTreeNode* left; struct BinaryTreeNode* right; }BTNode; BTNode* BuyNode(BTDataType x) { 
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode)); if (newnode == NULL) { 
    perror("malloc fail"); return NULL; } newnode->right = NULL; newnode->data = x; newnode->left = NULL; return newnode; } BTNode* CreatBinaryTree() { 
    BTNode* node1 = BuyNode(1); BTNode* node2 = BuyNode(2); BTNode* node3 = BuyNode(3); BTNode* node4 = BuyNode(4); BTNode* node5 = BuyNode(5); BTNode* node6 = BuyNode(6); node1->left = node2; node1->right = node4; node2->left = node3; node4->left = node5; node4->right = node6; return node1; } 

💥💥注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。

二、二叉树的三种遍历✨✨

1.前序

💫💫这里要注意访问叶子结点时要将它左右也就是NULL访问，这样才不会出差错。不能说它没有左右子树，而是它的孩子结点为NULL。

代码如下：

// 二叉树前序遍历 void PreOrder(BTNode* root) { 
    if (root)//如果root为NULL就不需要进入if语句直接退出函数 { 
    printf("%d\n", root->data); PreOrder(root->left); PreOrder(root->right); } } 

2.中序

代码如下：

// 二叉树中序遍历 void InOrder(BTNode* root) { 
    if (root) { 
    InOrder(root->left); printf("%d\n", root->data); InOrder(root->right); } } 

3.后序

代码如下：

// 二叉树后序遍历 void PostOrder(BTNode* root) { 
    if (root) { 
    PostOrder(root->left); PostOrder(root->right); printf("%d\n", root->data); } } 

三、小练习🥰🥰

四、结语🌹🌹

✨✨由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

以上就是二叉树前中后序的遍历啦~学习它对我们后续学习二叉树的操作有很大作用同时也帮我们复习和了解递归的使用，可谓一举两得，大家都get到了吗， 完结撒花 ~🥳🥳🎉🎉🎉

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2rx6jz7eu90kg