通信原理（一） 通信原理概述

大家好，欢迎来到IT知识分享网。

0、通信系统

数字通信系统模型：

1、通信方式

单工、双工与半双工

对于点与点之间的通信，按消息传递的方向与时间关系，通信方式可分为单工、半双工及全双工通信。

1. 单工通信:是指消息只能单方向传输的工作方式，如广播、遥测、遥控
2. 半双工通信:是指通信双方都能收发消息，但不能同时进行收和发的工作方式，如对讲机
3. 全双工通信:是指通信双方可同时进行收发消息的工作方式。 一般情况全双工通信的信道必须是双向信道

并行传输与串行传输

1. 并行传输:将码元序列在两条以上的并行信道上同时传输,节省传输时间、速度快且不需要另外的措施就实现了同步。缺点是需要n条通信线路，成本高。并行传输一般只用于设备之间的近距离通信，如计算机和打印机之间数据的传输。
2. 串行传输:将码元序列以串行方式一个接一个地在一条信道上传输，远距离数字传输常采用这种方式。优点是只需一条通信信道、成本低，缺点是速度慢，需要外加同步措施。

2、性能指标

2.1、有效性指标

• 模拟系统：有效带宽，同样的消息用不同的调制方式，则需要不同的频率宽度
• 数字系统：波特率和比特率、频带利用率

波特率和比特率
码元传输速率（波特率）：单位时间传输的码元的个数，单位是波特Baud
信息传输速率（比特率）：单位时间传输的比特的个数，单位是bit/s

频带利用率
单位带宽（每Hz）内的传输速率单位带宽(每Hz)内的传输速率， 用符号$\eta$或${\eta }_b$表示:
$$\eta =R_B/B$$$${\eta }_b=R_b/B$$式中，$B$为信道传输带宽;$R_B$为码元传输速率;$R_b$为信息传输速率。

2.2、可靠性指标

• 模拟系统：接收端信噪比
  不同调制方式在同样信道信噪比下所得到的解调后的输出信噪比是不同的。
  
• 数字系统：误码率和误信率

3、码

信源编码可看作信源符号集(消息)到码元集（码符号集）的一种映射

3.1、码字、码元、码长

• 码元（码符号）：一个脉冲信号就是一个码元，二进制码元（码元集元素个数为2）携带1bit信息，四进制码元携带2bit信息；码元是信号传输实体的最小单位
• 码字：码字是码元的组合
• 码长：组成码字的码元个数，平均码长可以衡量码的性能，即编码效率：$$\eta \triangleq \frac{H(X)}{\bar{n}logD}，\bar{n}为平均码长，D为码元集的元素个数$$

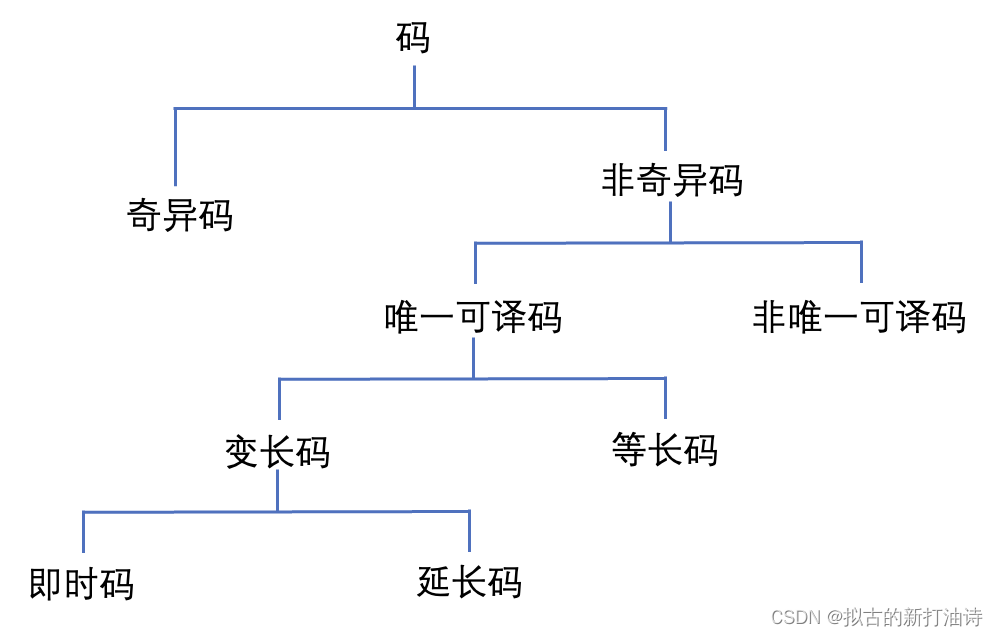
3.2、码的分类

• 非奇异码：信源符号和码字一一对应的码
• 唯一可译码：任意由码字组成的有限长序列都能恢复成唯一的信源序列的码；可保证无失真编码；可由克拉夫特不等式判断
• 即时码：任一码字都不是其他码字字头的码；即时码可用树图法构造

4、抽样与抽样定理

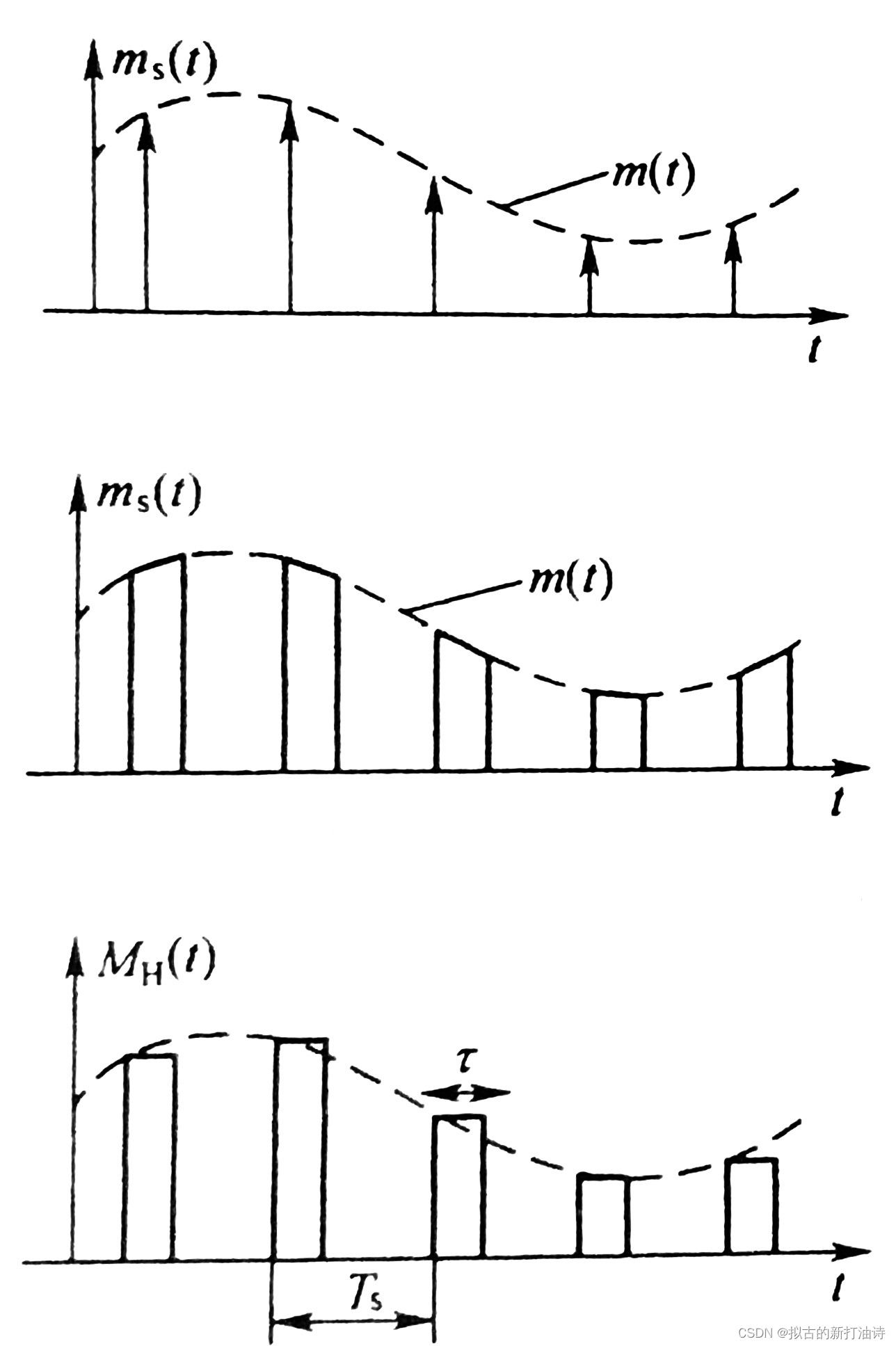
4.1、理想抽样和实际抽样

理想抽样：模拟信号与单位冲激序列相乘，实际无法实现。
自然抽样（曲顶抽样）：用矩形方波抽样，顶部随信号幅度变化
平顶抽样：用矩形方波抽样，顶部为抽样保持

4.2、抽样定理

对一个带宽有限的连续模拟信号进行抽样时，若抽样频率足够大，则抽样值能够完全代表原模拟信号，并能由这些抽样值恢复出原模拟信号。
$$\begin{array}{rl}低通抽样定理:& 一个频率在0\le f\le f_H的连续时间信号m(t)，\\ & 如果以T_s\le \frac{1}{2f_H}的间隔或f_s\ge 2f_H的频率对其进行抽样，\\ & 则m(t)将被这些抽样值完全确定。\\ & 最小抽样频率f_s=2f_H称为奈奎斯特频率，\\ & 最大抽样间隔T_s=\frac{1}{2f_H}称为奈奎斯特间隔。\end{array}$$

$$\begin{array}{rl}带通抽样定理:& 频率在f_L\le f\le f_H且f_L>B的连续时间信号m(t)，\\ & 其最小抽样频率f_s=2B\left(1+\frac{k}{n}\right)，\\ & 其中B为带宽，n、k分别为\frac{f_H}{B}的整数部分和小数部分。\end{array}$$

由于实际滤波器的不理想特性，实用的抽样频率必须比奈奎斯特大一些。例如，典型电话信号的最高频率通常限制在3400Hz，而抽样频率通常采用8000Hz。