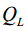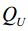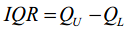大家好,欢迎来到IT知识分享网。
异常点、高杠杆点、强影响点
异常点:残差很大的点;
高杠杆点:远离样本空间中心的点;
强影响点:改变拟合回归方程特征的点。
注意:
A点:非异常点、高杠杆点、非强影响点
- A点在X空间中距离样本的中心较远,A是个高杠杆点;
- A点的位置在通过其他点的直线附近,残差很小,对拟合回归方程没有很大的影响,A点不是异常点也不是强影响点。
B点:异常点、非高杠杆点、强影响点
- B点在X空间中距离样本的中心较近,B不是高杠杆点;
- B点的残差很大,是异常点也是强影响点;
- 注意:B点的存在没有改变拟合直线的斜率,但是改变了拟合直线的截距。
C点:异常点、高杠杆点、强影响点
- C点的残差很大,所以点是一个异常点;
- C点在方向上远离其它的点的中心,所以点是一个高杠杆点;
- C点的引入实质性的改变拟合回归方程的特征,所以它是一个强影响点。
异常值处理:
- 对变量做一个描述性统计,进而查看哪些数据是不合理的,最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出了合理的范围。如:客户年龄的最大值为199岁,则该变量存在异常。
简单的统计量分析
- 若数据服从正态分布,在3
原则下,异常值被定义:一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值3
之外的值出现的概率为
,属于极个别小概率事件。
3原则
- 异常值定义:小于
或大于
的值。
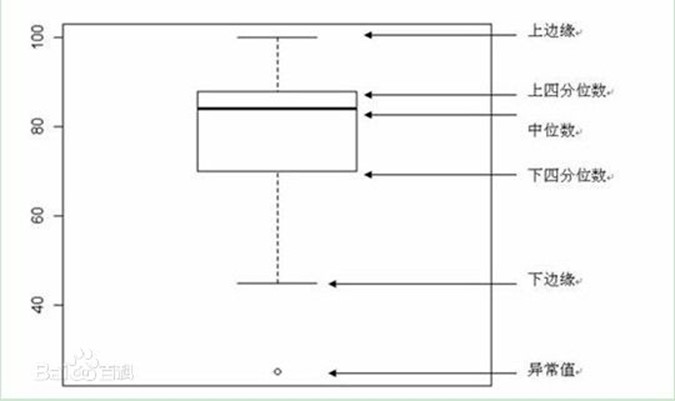
箱型图分析:下四分位数
:上四分位数
:四分位数间距,上下四分位数之差,其间包含全部观测值的一半
异常检测的混合模型方法
步骤如下:
1: 初始化:在时刻t=0,令Gt包含所有对象,而Bt为空;
令F(Gt,Bt)为好坏观测点划分的评价函数。
2: for 属于Gt的每个点x do
3: 将x从Gt移动到Bt,产生新的数据集合Gt+1和Bt+1。
4: 计算D的新的评价函数的值。
5: 计算差值: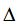
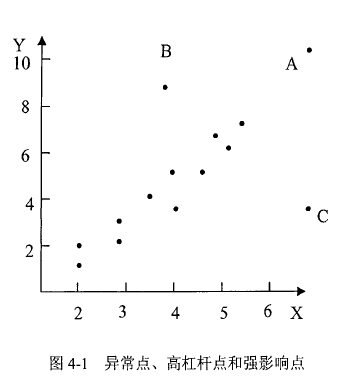
6: if 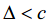
7: 将观测x分类为异常。
8: end if
9:end for
G可以理解为好的观测的集合,B理解为怀的观测的集合。
评价函数可以有很多种:如马氏距离、整个数据集的似然和对数似然等等
以马氏距离划分为例:
如果一种划分方式具有以下性质,我们认为这是合理的:
转载于:https://www.cnblogs.com/SevnChen/p/5024644.html
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/119290.html



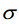 原则下,异常值被定义:一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值3
原则下,异常值被定义:一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值3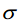 之外的值出现的概率为
之外的值出现的概率为 ,属于极个别小概率事件。
,属于极个别小概率事件。 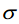 原则
原则 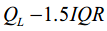 或大于
或大于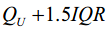 的值。
的值。