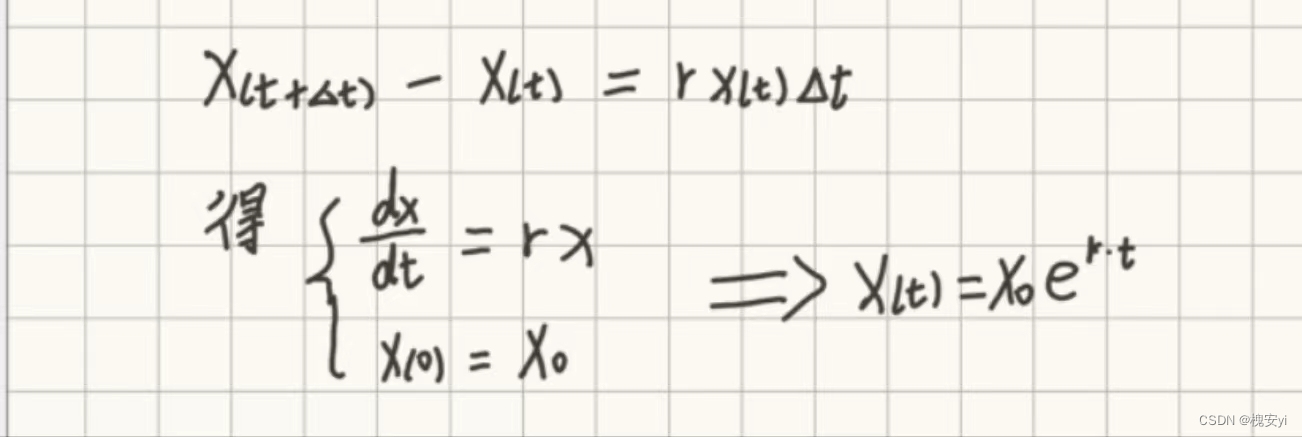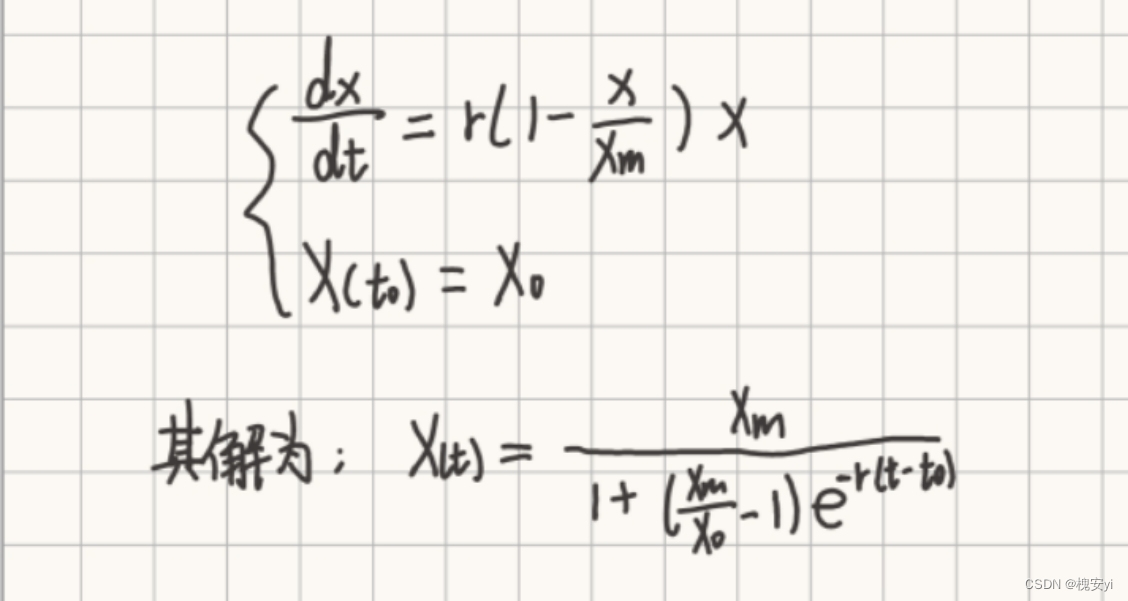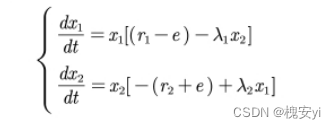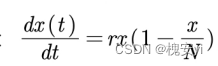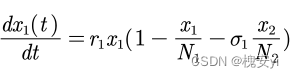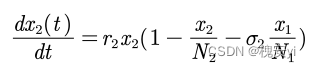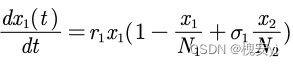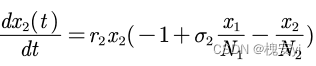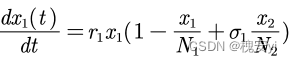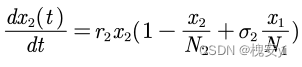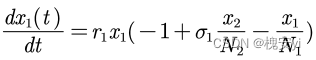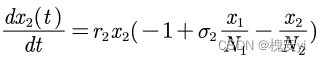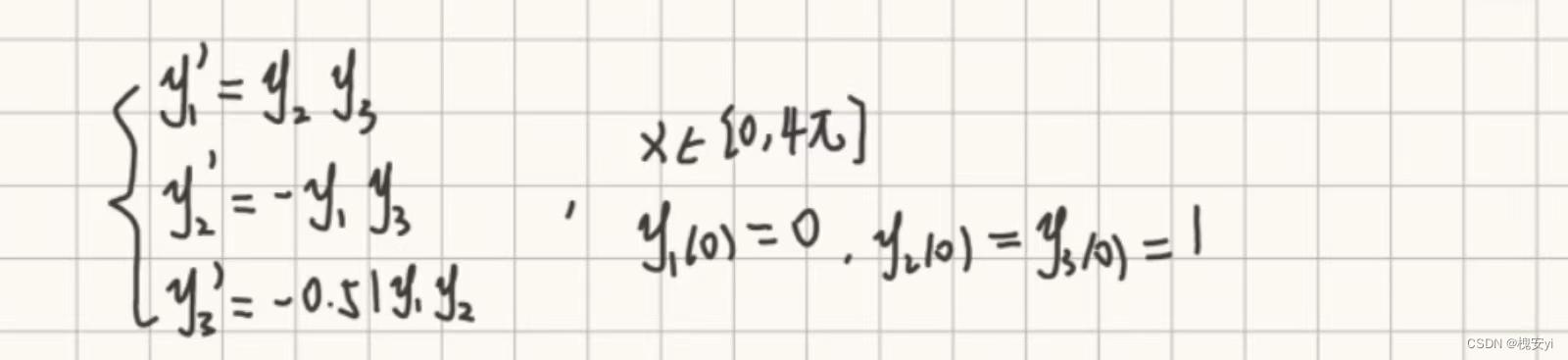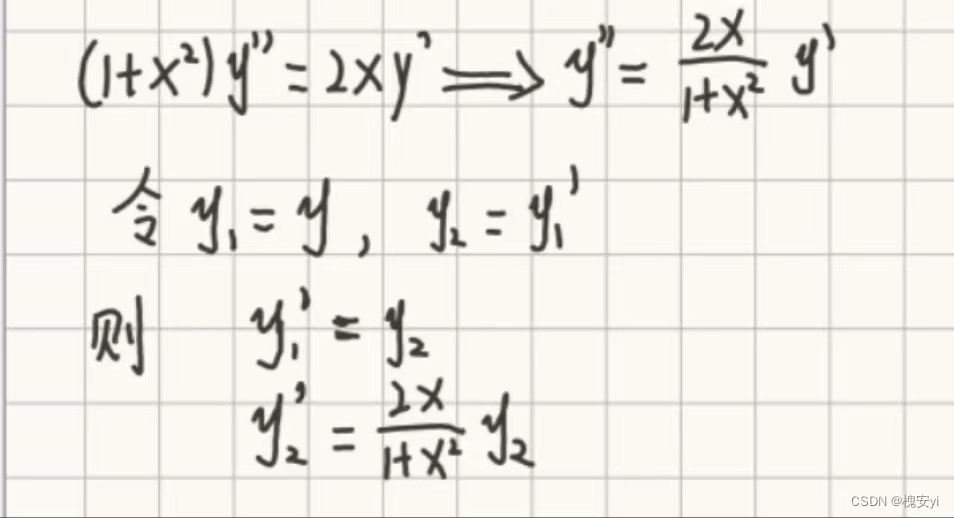【数学建模】微分方程模型

大家好，欢迎来到IT知识分享网。

1微分方程基本概念

1.1微分方程：含有未知函数及其导数的方程。

简单来说，微分方程指，含有未知函数及其导数的方程。

1.2微分方程分类：

（1）常微分方程：未知函数是一元函数

（2）偏微分方程：未知函数是多元函数

1.3微分方程的阶数：微分方程中所含导数或微分的最高阶数。

eg：是二阶微分方程

1.4微分方程的解：使得微分方程成立的函数（不唯一）

eg： $x^{2}$ 和 $x^{2}+1$ 都是一阶微分方程的解

1.5微分方程的通解和特解：特解不含常数；通解中所含的相互独立的任意常数的个数与微分方程的阶数相等。

eg： ${y}'-e^{x}=0$ 的特解为 $e^{x}$ ,通解为 $e^{x}$ +C

1.6初值条件：用来确定通解中常数的条件。

eg：若 ${y}'-e^{x}=0$ 且 y(0)=1 ,则通解 $e^{x}$ +C中C可以确定为0

1.7解析解和数值解

解析解：解的具体表达式

数值解：近似值

2微分方程模型

2.1人口预测模型——马尔萨斯模型、阻滞增长（Logistic）模型

2.1.1 马尔萨斯模型

模型假设：

建模求解：

2.1.2阻滞增长（Logistic）模型

模型假设：在马尔萨斯模型基础上，对人口增长率r进行修正

假设单位时间人口增长率为x的减函数，即r(x)=r-sx

假设当前环境和资源最大可能承受的人口数为xm，即x=xm时，增长率r(xm)=0

建模求解：

2.1.3总结

马尔萨斯模型适用于短期，未考虑环境因素。阻滞增长模型适用于中长期，且考虑外界因素。

2.2传染病模型

建立数学模型描述传染病的传播过程、分析传播规律、为预测和控制传染病提供信息和支持。

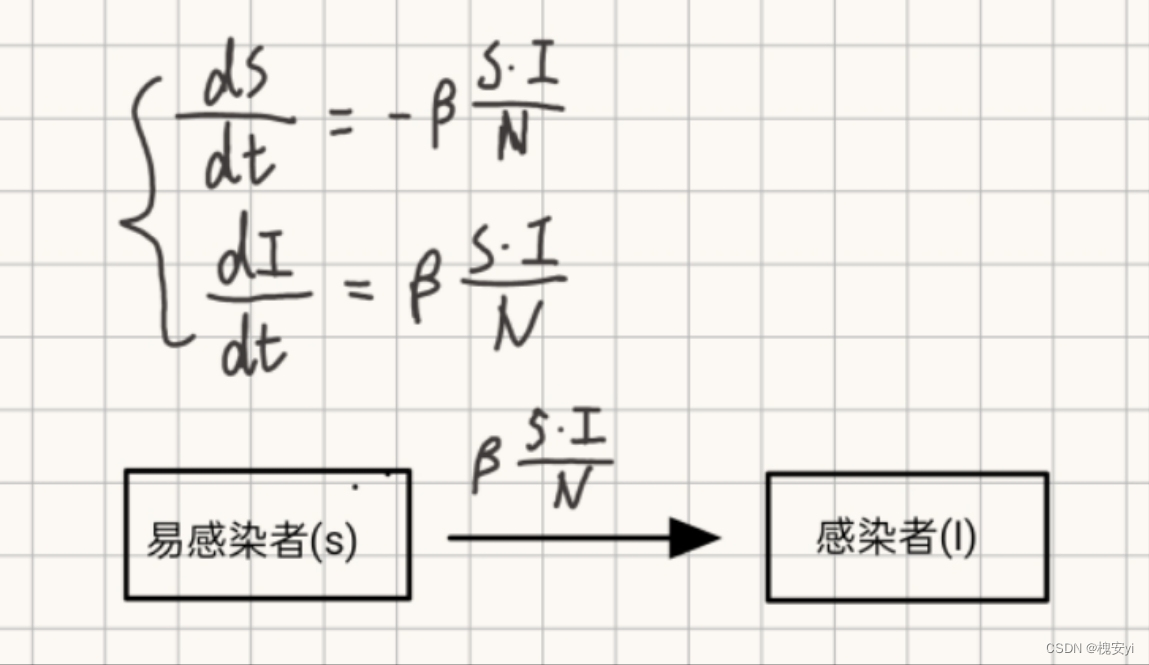
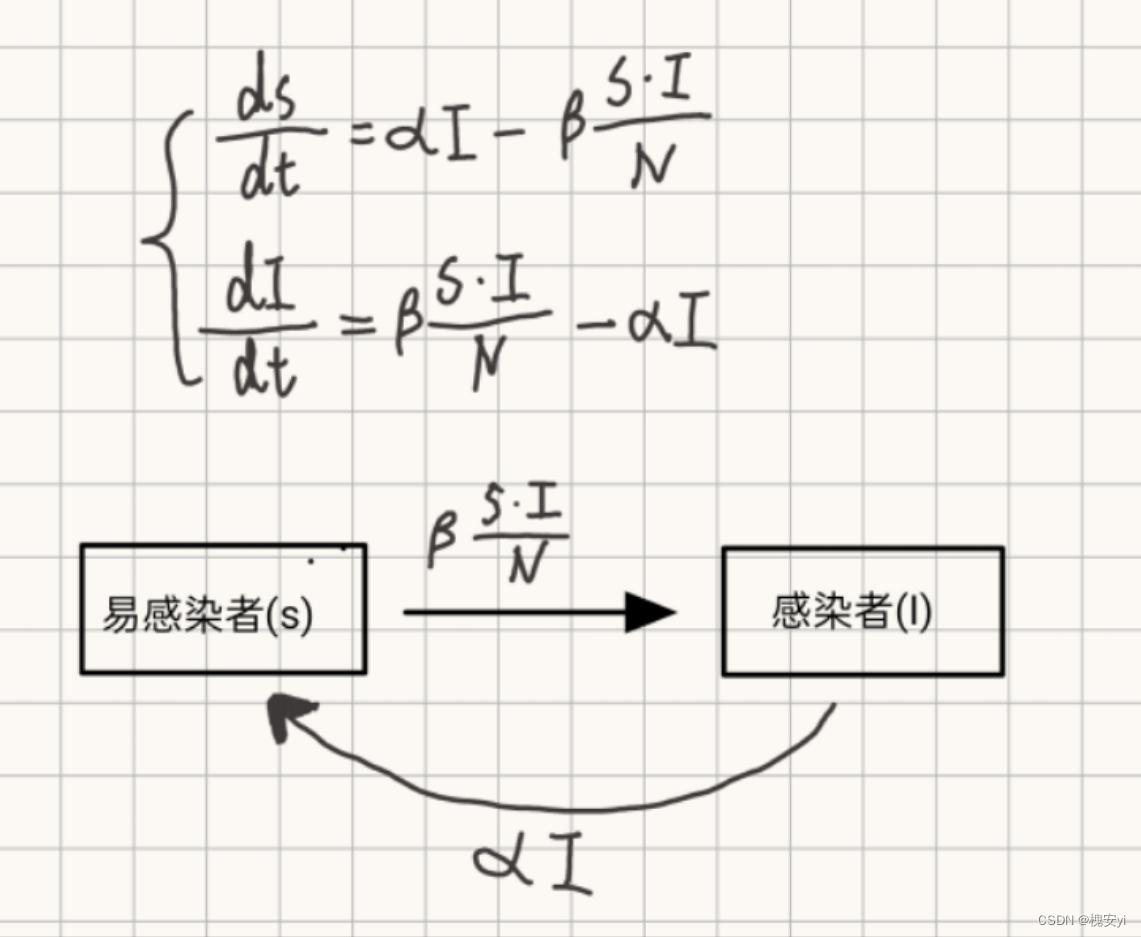
2.2.1 SI模型

SI模型中包括：

易感染者（S）也就是健康人

已感染者（I）也就是患者

模型假设：不考虑人口迁移和生死，设总人数N，则任意时刻N=S+I

假设单位时间内，易感染者S和已感染者I接触且被传染的强度为 $\beta$ ，且单位时间内，由S转换为I的人数为： $\beta \frac{S}{N}*\frac{I}{N}*N=\beta \frac{SI}{N}$

建模求解：

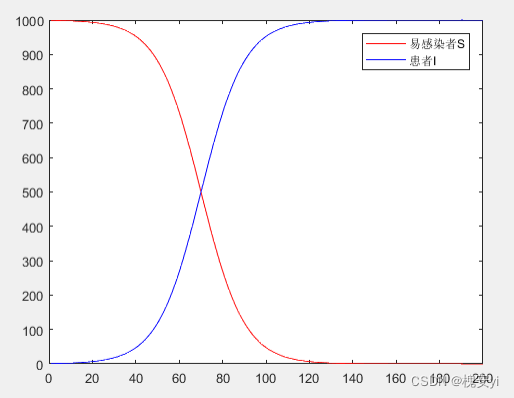
假设N=1000；最开始1人感染， $\beta$ 取0.1：

SI模型未考虑感染者被治愈的情况，最后所有人都变为感染者，不符合实际。

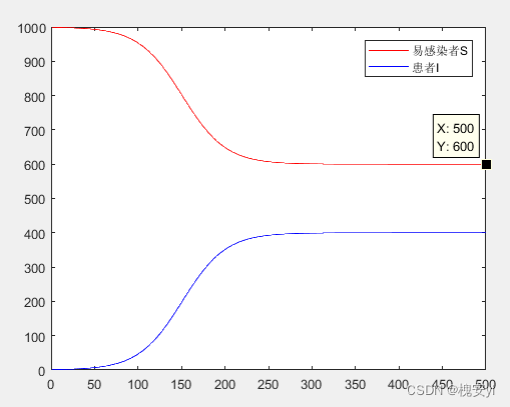
2.2.2 SIS模型

在SI模型的基础上，考虑感染者被治愈的情况，肯会经历：感染、恢复、感染、不断循环。

假定：总人口N，单位时间内感染人数为 $\beta \frac{SI}{N}$ ，由感染者（I）恢复为健康（S）的恢复率为 $\alpha$

建模求解：

假设N=1000；开始有1人感染； $\beta$ 取0.1； $\alpha$ 取0.06：

SIS模型考虑了病人被治愈的情况，未考虑被治愈的病人产生抗体，不会再次感染，即不参与循环的情况。

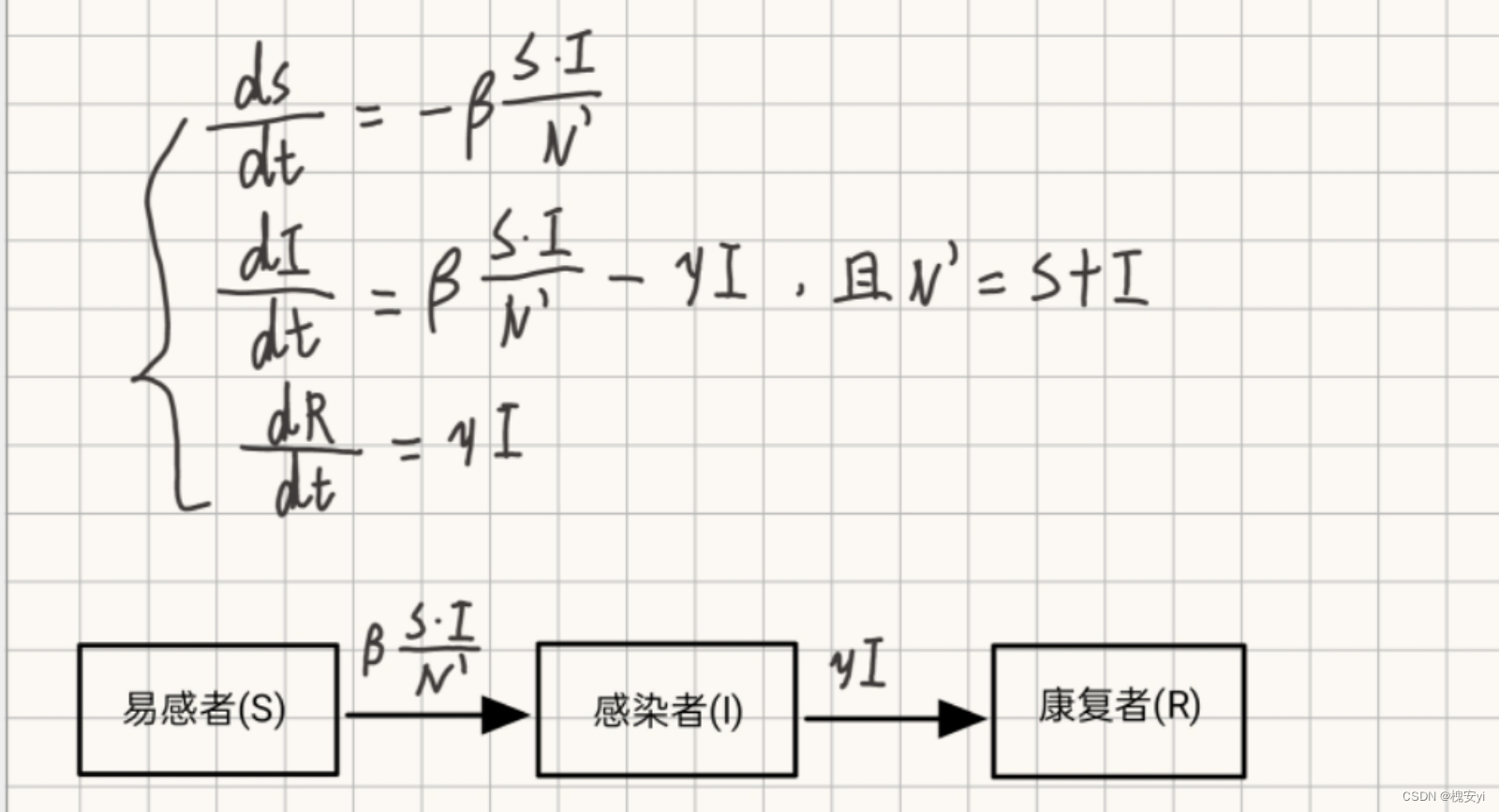
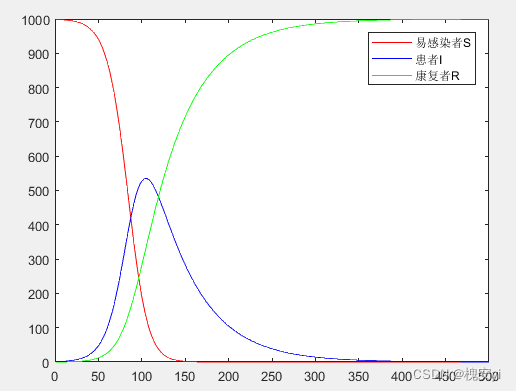
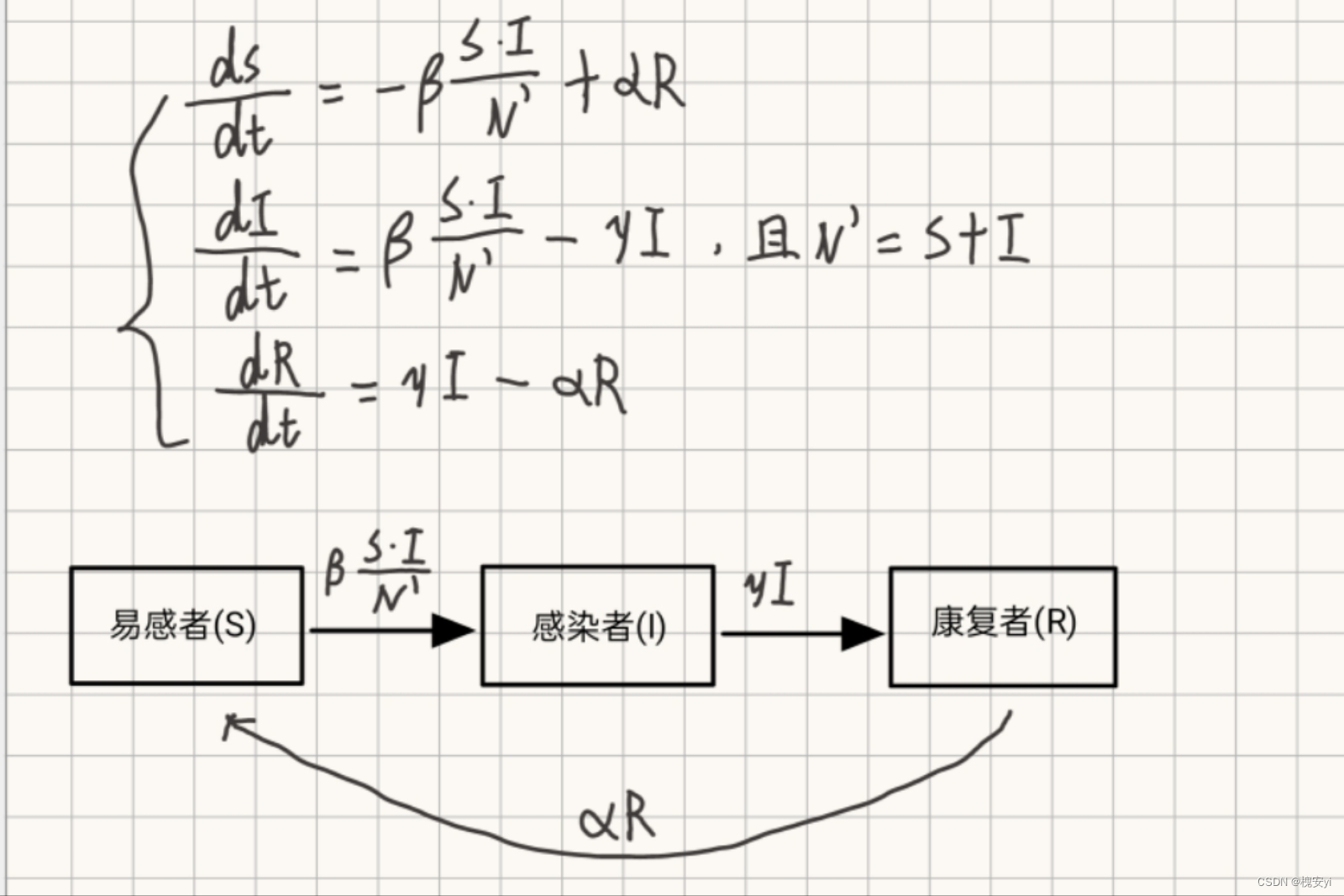
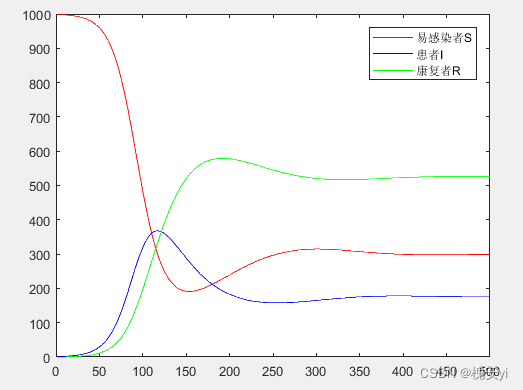
2.2.3 SIR模型

SIR模型中包括：

易感染者（S）也就是健康人

已感染者（I）也就是患者

已痊愈含抗体（R）未来不会被感染（不参与循环）

假定：总人口N；；单位时间内感染人数为 $\frac{\beta SI}{{N}'}$ ，由感染者（I）恢复为健康（S）的康复率为 $\gamma$

模型求解：

假设总人数1000；开始1人感染； $\beta$ 取0.1； $\gamma$ 取0.02：

2.2.4 SIRS模型

康复者R可能会以 $\alpha$ 的转化率再次转化为感染者R

假定：总人口N不变；总人口N，单位时间内感染人数为 $\beta \frac{SI}{N}$ ，由感染者（I）恢复为健康（S）的康复率为 $\gamma$ ；康复者（R)转变为易感者S的转化率为 $\alpha$

建模求解：

总人数1000； $\beta$ 取0.1；康复率 $\gamma$ 取0.03； $\alpha$ 取0.01：

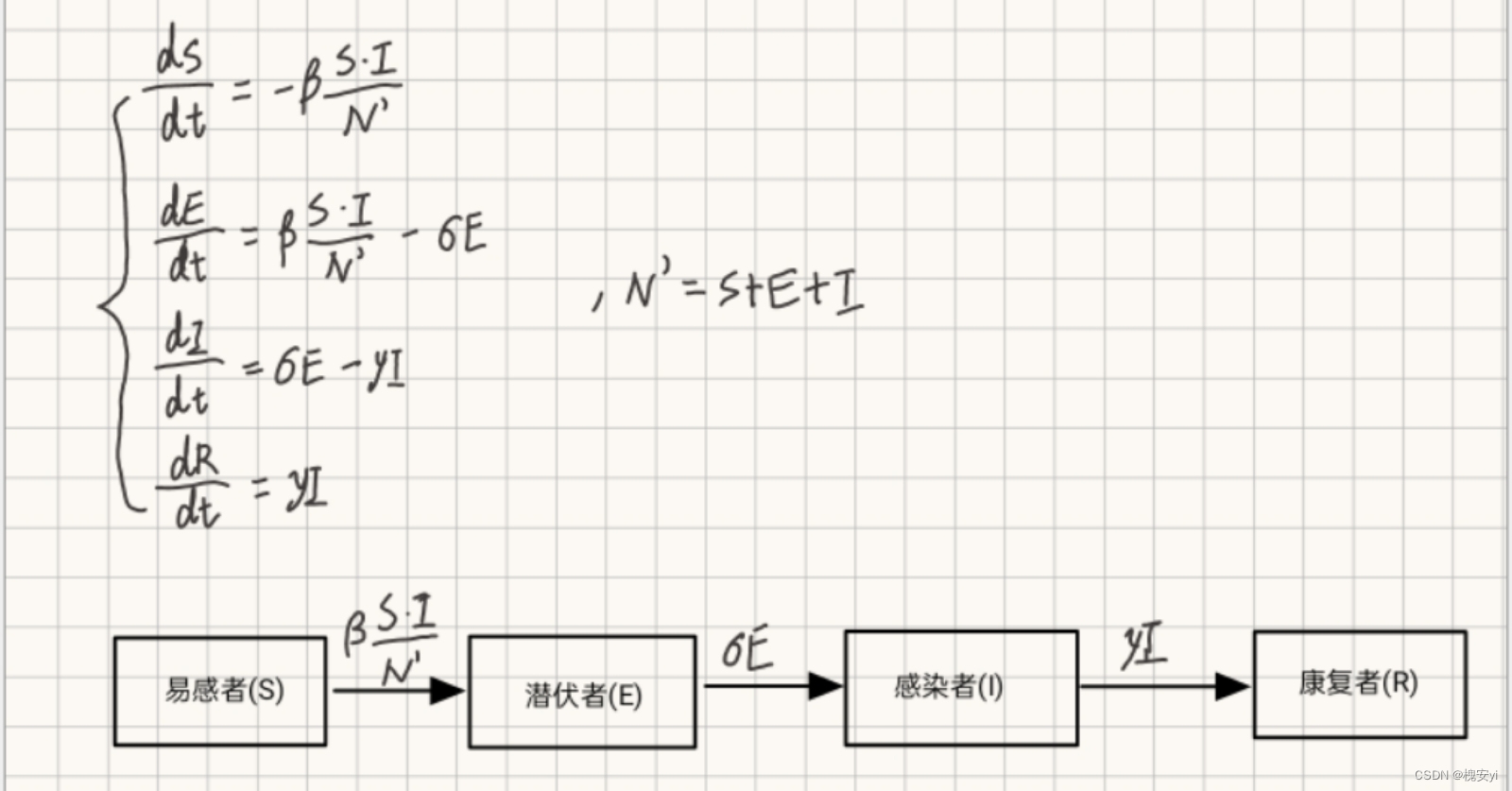
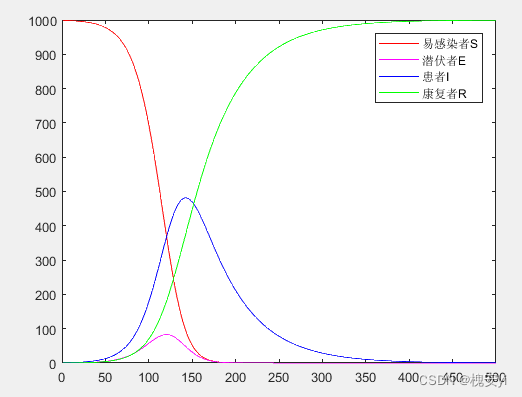
2.2.5 SEIR模型

引入潜伏者（E），即潜伏期人群

假定：总人口N；；单位时间内转变为潜伏者E的人数为 $\frac{\beta SI}{{N}'}$ ，潜伏者E转换为感染者I的速率为 $\sigma$ ；由感染者I康复为康复者R的康复率为 $\gamma$

建模求解：

总人数取1000，开始有1人感染， $\beta$ 取0.1； $\gamma$ 取0.02； $\sigma$ 取0.2：

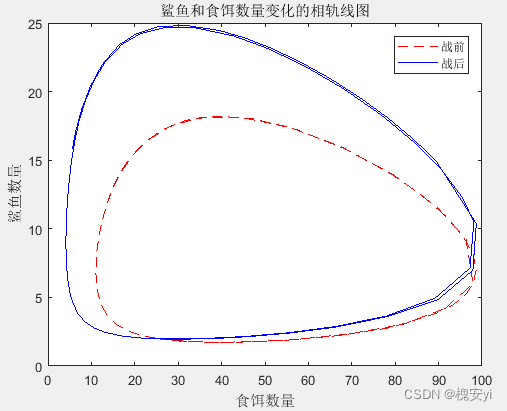
2.3捕食者猎物模型——地中海鲨鱼问题

设定：考虑人工捕获，食饵（即猎物）和捕食者在时刻 t 的数量分别记作 x1(t)和 x2(t) ，λ为捕食者捕食能力，e为人工捕食强度，r1为食饵的自然增长率，r2为捕食者的死亡率，有：

建模求解：

取x1(0)=25,x2(0)=2,战前e=0.3，战后e=0.1，r1=1,r2=0.02,λ1=0.1,λ2=0.02

2.4种群相互竞争模型（扩展应用到品牌竞争等）

就单个种群而言，常用阻滞增长模型描述数量变化：r是增长率，N是环境容纳量

若甲乙种群为竞争关系，我们需要考虑甲乙两个种群的相互影响，我们需要对“（）”内部分进行修正： $\sigma _{1 }$ 表示单位数量乙种群消耗供养甲的食物量为单位数量的甲消耗的供养甲的食物量的 $\sigma _{1 }$ 倍； $\sigma _{2}$ 表示单位数量甲种群消耗供养乙的食物量为单位数量的乙消耗的供养乙的食物量的 $\sigma _{2}$ 倍

2.5种群相互依存模型（国家相互贸易）

设定：

$\sigma _{1 }$ 表示单位数量乙种群提供供养甲的食物量为单位数量的甲消耗的供养甲的食物量的倍数； $\sigma _{2}$ 表示单位数量甲种群提供供养乙的食物量为单位数量的乙消耗的供养乙的食物量的倍数； r1、r2表示甲乙两种群的固有增长率（死亡率）

两个种群的相互依存情况有三种形式：

（1）甲可以独自生存，乙不能（或者反过来）

（2）甲乙均可以独自生存

（3）甲乙均不可以独自生存

（1）甲可以独自生存，乙不能

甲可以独自生存，且乙对甲有助长作用，r1为固有增长率，所以甲：

乙不能独自存活，假设他固有死亡率为r2，甲对乙有助长作用，所以乙：

（2）甲乙均可独自生存

r1、r2均为固有增长率

（3）甲乙均不能独自生存

r1、r2均为固有死亡率

3微分方程求解

3.1微分方程的解析解

dsolve('方程1'，'方程2'，...,'方程n','初始条件'，'自变量')

注：1）单双引号均可

2）字母D表示微分，D2表示二阶微分，D3表示三阶微分，后面跟要求解的因变量（Dy）

3）自变量可以指定，不写默认为t

4）方程中乘号“*”不能省略

5）初始值可以不给，这样求出来是通解

6）若微分方程较为复杂，可能得不到解析解，只能求数值解

eg：1）

dsolve('y-Dy=2*x','x')

2) $y-{y}'=2x,y\left ( 0 \right )=3$

dsolve('y-Dy=2*x','y(0)=3','x')

3) ${y}''+4{y}'+29y=0,y\left ( 0 \right )=0,{y}'\left ( 0 \right )=15$

dsolve('D2y+4*y*Dy+29*y','y(0)=0,Dy(0)=15','x')

4) $\frac{dx}{dt}=2x-3y+3z+t; \frac{dy}{dt}=4x-5y+3z+t; \frac{dz}{dt}=4x-4y+2z+t$

[x y z] = dsolve('Dx=2*x-3*y+3*z+t','Dy=4*x-5*y+3*z+t','Dz=4*x-4*y+2*z+t','t')

3.2微分方程数值解

[x,y]=solver('f',xs,y0,options)

注：1）x表示自变量

2）y表示函数值

3）代表求解函数，常用：ode45、ode45s。ode45s函数图像存在突变

4）xs=[x0,xf]代表自变量的初值和终值，也可以指定一个向量

5）y0表示函数初始值

6）options（可选）：options=odeset(‘reltol’,’rt’,’abstol’,at)，rt，at分别为设定的相对误差，默认为10e-3，10e-6

7）f表示由待解微分方程编写的m函数文件名，可以写成@f

8）x，y只是变量名，可以自己取名

9）使用matlab求解数值解，高阶微分方程必须转化为一阶

一阶微分方程数值解：1）化为标准型；2）带入函数

eg：1），y（0）=3，x范围[0,2]

1)化为标准型：

2)带入函数：

i)建立m文件，编辑f函数

function dy = f(x,y) % dy是标准化后左边的式子，x是式子右边的自变量，y是因变量 dy = y - 2*x; end

ii）新建m文件，计算

[x y] = ode45('f',[0,2],3); %x是自变量，y是因变量 figure(1) plot(x,y,'*-') axis([0 2 -inf inf]) grid on

2）方程组：

1）题目已经化为标准型

2）带入函数

i)编辑f函数

function dy = f(x,y) % dy是标准化后左边的式子，x是式子右边的自变量，y是因变量 dy = zeros(3,1); dy(1) = y(2)*y(3); dy(2) = -y(1)*y(3); dy(3) = -0.51*y(1)*y(2); end

ii)新建m文件，计算

[x, y] = ode45('f', [0 4*pi], [0 1 1]); % 这里的y是一个有3列的矩阵哦！x是自变量，y是因变量 plot(x, y(:,1), 'o', x, y(:,2), '*', x, y(:,3), '+') legend('y1','y2','y3') % 加上标注 axis([0, 4*pi, -inf, +inf]) % 设置横坐标范围为0-4pi，纵坐标范围不需要设置，写成-inf到+inf

高阶微分方程数值解：1）标准化，高阶转化为一阶；2）按一阶求解

eg：

1）标准化

2）带入函数

i）f函数

function dy=f(x,y) dy=zeros(2,1); dy(1)=y(2); dy(2)=(2*x)/(1+x*x)*y(2); end

ii)计算

[x,y]=ode45('f',[-2,2],[3,4])

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/123138.html

【数学建模】微分方程模型

相关推荐

发表回复