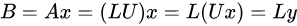理论总结-三次样条插值

大家好，欢迎来到IT知识分享网。

主要参考文献：三次样条(cubic spline)插值

0 前言

1、在每个分段小区间[x_i,x_i+1]上，S(x)=S_i(x)都是一个三次方程，其中i=0,1…,n-1；

1 思路

现在的目标是：【通过找出4n个方程去求解4n个未知数】

现在总共有4n-2个方程了，还差两个方程就可以解出所有未知数。

剩余的两个方程将通过边界条件得到。有三种边界条件：

2 推导

S_i(x)及其一阶导数、二阶导数分别为：

1、由：

可得：

2、步长设为：

由S_i(x_i+1)=y_i+1可得：

3、由S’_i(x_i+1)=S’_i+1(x_i+1)可得：

有：

4、由S”_i(x_i+1)=S”_i+1(x_i+1)可得：

设：

可得：

5、由上面1-4的a_i、c_i、d_i的公式，即：

代入到：

可得：

6、于是将a_i、b_i、c_i、d_i的公式代入到：

可得：

下面通过三种不同的边界条件分别构造三个以m为未知数的线性方程组。

2.1 自然边界

2.2 固定边界

2.3 非扭结边界

3 总结

3、解矩阵方程，求得二次微分值m_i。该矩阵为三对角矩阵，常见解法为高斯消元法，可以对系数矩阵进行LU分解，分解为单位下三角矩阵和上三角矩阵，即：

4、计算样条曲线的系数：

5、在每个子区间：

中，创建方程：

结束

END