【图论】 图论基础

大家好，欢迎来到IT知识分享网。

目录

一. 图的概念

二. 建图方法

1. 邻接矩阵

2. 邻接表

3. 例题分析

3.1 小鑫的难题

3.2 小鑫的难题2

3.3 小鑫的难题3

三. 图的遍历

1. 深度搜索优先（DFS）

1.1 递归实现与非递归实现

1.2 邻接矩阵实现

2. 广度搜索优先（BFS）

3. 例题分析

3.1 迷宫

3.2 魔兽传说

3.3  小鑫的女朋友被魔王抢走了

3.4 广度优先搜索遍历

3.5 广度优先搜索遍历2

3.6 魔兽传说2

3.7 最短时间

3.8 高楼电梯

3.9 PTA 喊山

一. 图的概念

图是一种由“顶点”组成的抽象网络，网络中的各顶点可以通过“边”实现彼此的连接，表示两顶点有关联。最基本的图通常被定义为“无向图”，与之对应的则被称为“有向图”，两者唯一的区别在于有向图中的边是有方向性的。总的来说，图（Graph）G由两个集合顶点V（Vertex）和边E（Edge）组成，记作G=（V,E）。

二. 建图方法

1. 邻接矩阵

邻接矩阵方法使用数组G[i][j]来表示i顶点和j顶点是否连通，若边有权值，则可将G初始化为INF，用G来保存权值！邻接矩阵简单直接好操作但是消耗内存，占用时间，对于小数量的题目可以采用。

2. 邻接表

邻接矩阵是一种不错的图存储结构，但是对于边数相对较少的图，这种结构存在空间上的极大浪费。因此，找到一种数组与链表相结合的存储方法称为邻接表。该方法的核心代码如下：

struct Node { int date; Node *next; }; Node *paint[maxn]; //建图 if(paint[a]==NULL)//此节点没有就更新！ { paint[a]=new Node; paint[a]->date=b; paint[a]->next=NULL; } else { p=new Node; p->date=b; p->next=paint[a]->next;//把所有边存下来连接起来！ paint[a]->next=p;//关键！ }

3. 例题分析

3.1 小鑫的难题

Problem Description

解决图论问题，首先就要思考用什么样的方式存储图。但是小鑫却怎么也弄不明白如何存图才能有利于解决问题。你能帮他解决这个问题么？

Input

有多组输入，到文件结尾。

每一组第一行有两个数n、m表示n个点，m条有向边。接下来有m行，每行两个数u、v代表u到v有一条有向边。第m+2行有一个数q代表询问次数，接下来q行每行有一个询问，输入两个数为a，b。

注意：点的编号为0~n-1，2<=n<=5000 ，n*(n-1)/2<=m<=n*(n-1)，0<=q<=，a!=b，输入保证没有自环和重边

Output

对于每一条询问，输出一行。若a到b可以直接连通输出Yes，否则输出No。

Example

#include <iostream> #include<cstdio> #include<cstring> using namespace std; const int maxn=5000; bool connection[maxn][maxn];//int会超时，bool一个字节，所以比较快？？ int main() { int n,m; while(scanf("%d%d",&n,&m)!=EOF) { memset(connection,0,sizeof(connection));//用cin和cout会超时！而用scanf和printf不会！说明了cin和cout很慢了！ for(int i=0;i<m;i++) { int a,b; scanf("%d%d",&a,&b); connection[a][b]=1;//有边标记即可，若为无向图则需要双向标记！ } int q; scanf("%d",&q); while(q--) { int a,b; scanf("%d%d",&a,&b); if(connection[a][b]==1) printf("Yes\n"); else printf("No\n"); } } return 0; }

3.2 小鑫的难题2

Problem Description

解决图论问题，首先就要思考用什么样的方式存储图。但是小鑫却怎么也弄不明白如何存图才能有利于解决问题。你能帮他解决这个问题么？

Input

有多组输入，到文件结尾。

每一组第一行有两个数n、m表示n个点，m条有向边。接下来有m行，每行两个数u、v代表u到v有一条有向边。第m+2行有一个数q代表询问次数，接下来q行每行有一个询问，输入两个数为a，b。

注意：点的编号为0~n-1，2<=n<= ，0<=m<=，0<=q<=，a!=b，输入保证没有自环和重边

Output

对于每一条询问，输出一行。若a到b可以直接连通输出Yes，否则输出No。

Example

#include <iostream> #include<cstdio> #include<cstring> using namespace std; const int maxn=;//数据过大，使用邻接矩阵超内存，只能使用邻接表！！ struct Node { int date; Node *next; }; Node *paint[maxn]; int main() { int n,m; while(scanf("%d%d",&n,&m)!=EOF) { Node *p,*t; memset(paint,0,sizeof(paint)); for(int i=0;i<m;i++) { int a,b; scanf("%d%d",&a,&b); if(paint[a]==NULL)//此节点没有就更新！ { paint[a]=new Node; paint[a]->date=b; paint[a]->next=NULL; } else { p=new Node; p->date=b; p->next=paint[a]->next;//把所有边存下来连接起来！ paint[a]->next=p; } } int q; scanf("%d",&q); while(q--) { int a,b; scanf("%d%d",&a,&b); t=paint[a]; bool judge=false; while(t!=NULL) { if(t->date==b) { judge=true; break; } t=t->next;//查找时顺着链子依次查找！ } if(judge) printf("Yes\n"); else printf("No\n"); } } return 0; }

3.3 小鑫的难题3

（1）问题描述

Problem Description

解决图论问题，首先就要思考用什么样的方式存储图。但是小鑫却怎么也弄不明白如何存图才能有利于解决问题。你能帮他解决这个问题么？

Input

多组输入，到文件结尾。

每一组第一行有两个数n、m表示n个点，m条有向边。接下来有m行，每行两个数u、v、w代表u到v有一条有向边权值为w。第m+2行有一个数q代表询问次数，接下来q行每行有一个询问，输入一个数为a

注意：点的编号为0~n-1，2<=n<= ，0<=m<=，0<=q<=，u!=v，w为int型数据。输入保证没有自环和重边

Output

 对于每一条询问，输出一行两个数x，y。表示排序后第a条边是由x到y的。对于每条边来说排序规则如下：

1. 权值小的在前。
2. 权值相等的边出发点编号小的在前
3. 权值和出发点相等的到达点编号小的在前

注：边的编号自0开始

Example

（2）题解代码

        考察快速排序，邻接矩阵和邻接表都不能排序，直接用结构体表示。

#include <iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=; struct Node { int start,ending,val; bool operator<(const Node &A)const{//重载一下 if(val!=A.val)return val<A.val; else if(start!=A.start)return start<A.start; else return ending<A.ending; } }node[maxn]; int main() { int n,m; while(cin>>n>>m) { for(int i=0;i<m;i++) { int a,b,v; scanf("%d%d%d",&a,&b,&v); node[i].start=a; node[i].ending=b; node[i].val=v; } sort(node,node+m);//！ int q; scanf("%d",&q); while(q--) { int instruct; scanf("%d",&instruct); printf("%d %d\n",node[instruct].start,node[instruct].ending); } } return 0; } 

三. 图的遍历

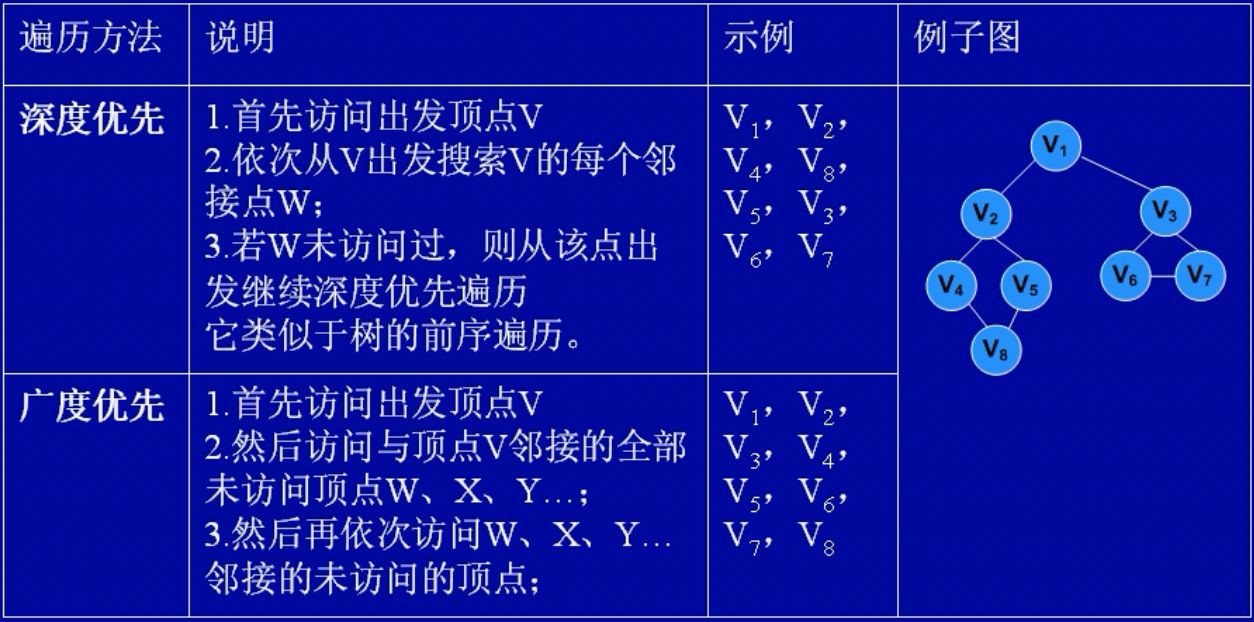
        由于图的存储方式有邻接矩阵和邻接表，所以图的遍历也有所不同。但是图的遍历分为深度遍历（DFS）和广度遍历（BFS）。由名字就可以看出，DFS是一条路探索到尽头，而BFS是由点扩散探索！其中，DFS常用于可否到达或者联通块问题，而BFS常用于最短路迷宫问题。

1. 深度搜索优先（DFS）

        DFS从图中某个结点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。其基本实现思想如下：

（1）访问顶点v；

（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；

（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

1.1 递归实现与非递归实现

（1）递归实现

（1）访问顶点v；visited[v]=1；//算法执行前visited[n]=0

（2）w=顶点v的第一个邻接点；

（3）while（w存在）  

           if（w未被访问）

                   从顶点w出发递归执行该算法； 
           w=顶点v的下一个邻接点；

（2）非递归实现

 （1）栈S初始化；visited[n]=0；

 （2）访问顶点v；visited[v]=1；顶点v入栈S

 （3）while(栈S非空)

            x=栈S的顶元素(不出栈)；

            if(存在并找到未被访问的x的邻接点w)

                    访问w；visited[w]=1；

                    w进栈;

            else

                     x出栈；

1.2 邻接矩阵实现

（1）邻接矩阵递归实现

void dfs(int p) { vis[p]=1; for(int j=1; j<=n; j++) { if(sign[p][j]&&!vis[j]) { dfs(j); } } }

（2）邻接矩阵栈实现

void DFS1(MGraph G,int v)   //非递归实现 {     stack<int> s;    printf("%d ",v);        //访问初始结点 visited[v]=true; s.push(v); //入栈    while(!s.empty())    {           int i,j;          i=s.top();          //取栈顶顶点         for(j=0;j<G.n;j++)  //访问与顶点i相邻的顶点         {            if(G.edges[i][j]!=0&&visited[j]==false)            {                printf("%d ",j);     //访问                visited[j]=true;                 s.push(j); //访问完后入栈                break;               //找到一个相邻未访问的顶点，访问之后则跳出循环          }       }        if(j==G.n)                   //如果与i相邻的顶点都被访问过，则将顶点i出栈       s.pop();    } }

2. 广度搜索优先（BFS）

        BFS是一个分层搜索的过程和二叉树的层次遍历十分相似，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。它是按照以某点为中心向周围扩散的顺序，因此他第一个碰到目的地的长度就是最短路！！其基本实现思想如下： 

（1）顶点v入队列。

（2）当队列非空时则继续执行，否则算法结束。

（3）出队列取得队头顶点v；访问顶点v并标记顶点v已被访问。

（4）查找顶点v的第一个邻接顶点col。

（5）若v的邻接顶点col未被访问过的，则col入队列。

（6）继续查找顶点v的另一个新的邻接顶点col，转到步骤（5）。

直到顶点全部处理完，队列为空转到(2)

注意：广度优先遍历图是以顶点v为起始点，由近至远，依次访问和v有路径相通而且路径长度为1，2，……的顶点。为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问，需设置队列存储访问的顶点。其伪代码如下：

（1）初始化队列Q；visited[n]=0；

（2）访问顶点v；visited[v]=1；顶点v入队列Q；

（3） while（队列Q非空）   

              v=队列Q的对头元素出队；

              w=顶点v的第一个邻接点；

             while（w存在） 

                     如果w未访问，则访问顶点w；

                     visited[w]=1；

                     顶点w入队列Q；

                     w=顶点v的下一个邻接点。

3. 例题分析

3.1 迷宫

Problem Description

一个由n * m 个格子组成的迷宫，起点是(1, 1)， 终点是(n, m)，每次可以向上下左右四个方向任意走一步，并且有些格子是不能走动，求从起点到终点经过每个格子至多一次的走法数。

Input

第一行一个整数T 表示有T 组测试数据。(T <= 110)

对于每组测试数据:

第一行两个整数n, m，表示迷宫有n * m 个格子。(1 <= n, m <= 6, (n, m) !=(1, 1) ) 接下来n 行，每行m 个数。其中第i 行第j 个数是0 表示第i 行第j 个格子可以走，否则是1 表示这个格子不能走，输入保证起点和终点都是都是可以走的。

任意两组测试数据间用一个空行分开。

Output

对于每组测试数据，输出一个整数R，表示有R 种走法。

#include <iostream> #include<cstdio> #include<cstring> using namespace std; int maps[10][10];//地图 int vis[10][10];//标记是否走过 int dh[]={-1,1,0,0}; int dl[]={0,0,-1,1}; int sum,n,m; void dfs(int a,int b) { if(a==n&&b==m)//走到终点 { sum++; return; } for(int i=0;i<4;i++) { int da=a+dh[i],db=b+dl[i]; if(da>=1&&da<=n&&db>=1&&db<=m&&!maps[da][db]&&!vis[da][db])//满足条件 { vis[da][db]=1;//标记 dfs(da,db);//DFS vis[da][db]=0;//回溯 } } } int main() { int T; cin>>T; while(T--) { memset(maps,0,sizeof(maps)); memset(vis,0,sizeof(vis)); sum=0; cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) cin>>maps[i][j]; } vis[1][1]=1; dfs(1,1); cout<<sum<<endl; } return 0; } 

3.2 魔兽传说

（1）问题描述

Problem Description

在古老的魔兽传说中，有两个军团，一个叫天灾，一个叫近卫。在他们所在的地域，有n个隘口，编号为1..n，某些隘口之间是有通道连接的。其中近卫军团在1号隘口，天灾军团在n号隘口。某一天，天灾军团的领袖巫妖王决定派兵攻打近卫军团，天灾军团的部队如此庞大，甚至可以填江过河。但是巫妖王不想付出不必要的代价，他想知道在不修建任何通道的前提下，部队是否可以通过隘口及其相关通道到达近卫军团展开攻击。由于n的值比较大（n<=1000），于是巫妖王找到了擅长编程的你 =_=，请你帮他解决这个问题，否则就把你吃掉变成他的魔法。为了拯救自己，赶紧想办法吧。

Input

输入包含多组，每组格式如下。

第一行包含两个整数n,m（分别代表n个隘口，这些隘口之间有m个通道）。

下面m行每行包含两个整数a，b；表示从a出发有一条通道到达b隘口（注意：通道是单向的）。

Output

如果天灾军团可以不修建任何通道就到达1号隘口，那么输出YES，否则输出NO。

（2）题解代码

        注意区分上题的回溯法与本题的区别，上题是求到目的地的路数，因此需要回溯尝试多条路，而本题只需判断是否可到达，所以DFS即可。如可以到达，一次DFS肯定可以深搜到，否则就说明每一个点的终点都不是目的地。因此标记不需要回溯，本题采用邻接表。

#include <iostream>//不要把回溯法和DFS搞混了！！！ #include<cstring> #include<cstdio> using namespace std; const int maxn=1000; int n,m; bool vis[maxn]; bool sign; struct Node { int date; Node *next; }; Node *node[maxn]; void dfs(int a) { if(a==1)//到达即可 { sign=true; return; } vis[a]=1; Node *t=node[a]; while(t) { if(!vis[t->date]) dfs(t->date); t=t->next; } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { sign=false; memset(node,0,sizeof(node)); memset(vis,0,sizeof(vis)); for(int i=0;i<m;i++) { int a,b; scanf("%d%d",&a,&b); if(node[a]==NULL) { node[a]=new Node; node[a]->date=b; node[a]->next=NULL; } else { Node *p=new Node; p->date=b; p->next=node[a]->next; node[a]->next=p; } } Node *t=node[n]; vis[n]=1; dfs(n); if(sign) printf("YES\n"); else printf("NO\n"); } return 0; } 

3.3  小鑫的女朋友被魔王抢走了

（1）问题描述

Problem Description

魔王留给小鑫一张n*m大的表，上面有各种各样的颜色，用A-Z这26个字母来表示。魔王留给他一个任务，如果小鑫可以在这张表中找出任意一个长度大于1的环，并且这个环的颜色是相同的，魔王就把小鑫的女朋友还给他。为了从魔王手中夺回他的女朋友，小鑫请你帮忙，你能帮帮他吗？

Input

Output
如果可以救回他的女朋友，输出Yes，否则输出No

（2）题解代码

        经典DFS联通块，但是要注意几个小细节：一是还是要注意回溯与DFS的区别，如果可以联通，那么一个DFS就可以把某点周围所有同色的点标记，能不能构成环也就自然明了。因此标记不用回溯！类似uva油田。二是在上下左右行走时，这个点的来的方向不能再走了，所以要加一个标记！

#include <iostream> #include<cstring> #include<cstdio> using namespace std; char maps[201][201]; int vis[201][201];//不用再回溯为0，因为深度搜索尽力的搜索任何一个可能的联通块，如果在这个搜索里不行，那么下一个肯定也不行！！！ int dx[]= {-1,1,0,0}; int dy[]= {0,0,-1,1}; int notd[]={1,0,3,2};//不能走标记，走dx[0]的时候下一个点不能走dx[1]，以此类推； int n,m; bool sign; void dfs(int a,int b,int d) { if(sign) return; for(int i=0;i<4;i++) { if(i==d)continue; int mx=a+dx[i]; int my=b+dy[i]; if(mx>=1&&mx<=n&&my>=1&&my<=m&&maps[mx][my]==maps[a][b]) { if(vis[mx][my])//找到某个已经走过的点，形成了环！ { sign=true; return; } vis[mx][my]=1; dfs(mx,my,notd[i]);//不能走notd[i] } } } int main() { while(cin>>n>>m) { sign=false; memset(maps,0,sizeof(maps)); memset(vis,0,sizeof(vis)); for(int i=1; i<=n; i++) { for(int j=1; j<=m; j++) cin>>maps[i][j]; } for(int i=1; i<=n; i++) { for(int j=1; j<=m; j++) { if(!vis[i][j]) { vis[i][j]=1; dfs(i,j,-1); } if(sign) break; } if(sign) break; } if(sign) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; } 

3.4 广度优先搜索遍历

Problem Description

给定一个无向连通图，顶点编号从0到n-1，用广度优先搜索(BFS)遍历，输出从某个顶点出发的遍历序列。(同一个结点的同层邻接点，节点编号小的优先遍历）

Input

Output

输出有n行，对应n组输出，每行为用空格隔开的k个整数，对应一组数据，表示BFS的遍历结果（请使用邻接矩阵）

#include <iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int maxn=1000; int G[maxn][maxn]; int vis[maxn]; int n,m,t; void BFS(int a) { vis[a]=1; cout<<a; queue<int> que; que.push(a); while(!que.empty()) { int k=que.front(); que.pop(); for(int i=0;i<n;i++) { if(G[k][i]&&!vis[i]) { cout<<" "<<i; vis[i]=1; que.push(i); } } } cout<<endl; } int main() { int T; cin>>T; while(T--) { cin>>n>>m>>t; memset(G,0,sizeof(G)); memset(vis,0,sizeof(vis)); for(int i=0;i<m;i++) { int a,b; cin>>a>>b; G[a][b]=G[b][a]=1; } BFS(t); } return 0; } 

3.5 广度优先搜索遍历2

（1）问题描述

Problem Description

定一个无向连通图，顶点编号从0到n-1，用广度优先搜索(BFS)遍历，输出从某个顶点出发的遍历序列。(同一个结点的同层邻接点，节点编号小的优先遍历）

Input

Output

输出有n行，对应n组输出，每行为用空格隔开的k个整数，对应一组数据，表示BFS的遍历结果。（请使用邻接表）

（2）题解代码

        使用邻接表BFS时该题注意：1.注意无向图，邻接表双向建立！2.如何用邻接表进行由小到大呢？可以对每个点的表进行排序，按顺序指向的点就是由小到大的点！

#include <iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int maxn=1010; struct Node { int date; Node *next; }; Node *node[maxn]; int vis[maxn]; int k,m,t; void BFS(int a) { vis[a]=1; cout<<a; queue<int> que; que.push(a); for(int i=0;i<m;i++)//每个点都冒泡排序！！该点的联通点由小到大排列（这里差点忘了冒泡排序怎么写QAQ，快排用多了要复习巩固了QAQ） { for(Node *p=node[i];p!=NULL;p=p->next) { for(Node *q=p->next;q!=NULL;q=q->next) { if(p->date>q->date) { int temp=p->date; p->date=q->date; q->date=temp; } } } } //cout<<"yes"<<endl; while(!que.empty())//BFS { int u=que.front(); que.pop(); Node *mm=node[u]; while(mm) { if(!vis[mm->date]) { vis[mm->date]=1; cout<<" "<<mm->date; que.push(mm->date); } mm=mm->next; } } } int main() { int T; cin>>T; while(T--) { memset(node,0,sizeof(node)); memset(vis,0,sizeof(vis)); cin>>k>>m>>t; for(int i=1;i<=m;i++) { int a,b; cin>>a>>b; if(node[a]==NULL)//建立双向邻接表 { node[a]=new Node; node[a]->date=b; node[a]->next=NULL; } else if(node[a]!=NULL) { Node *p=new Node; p->date=b; p->next=node[a]->next; node[a]->next=p; } if(node[b]==NULL) { node[b]=new Node; node[b]->date=a; node[b]->next=NULL; } else if(node[b]!=NULL) { Node *p=new Node; p->date=a; p->next=node[b]->next; node[b]->next=p; } } BFS(t); cout<<endl; } return 0; } 

3.6 魔兽传说2

Problem Description

在古老的魔兽传说中，有两个军团，一个叫天灾，一个叫近卫。在他们所在的地域，有n个隘口，编号为1..n，某些隘口之间是有通道连接的。其中近卫军团在1号隘口，天灾军团在n号隘口。某一天，天灾军团的领袖巫妖王决定派兵攻打近卫军团，天灾军团的部队如此庞大，甚至可以填江过河。但是巫妖王不想付出不必要的代价，他想知道在不修建任何通道的前提下，部队是否可以通过隘口及其相关通道到达近卫军团展开攻击；如果可以的话，最少需要经过多少通道。由于n的值比较大（n<=1000），于是巫妖王找到了擅长编程的你 =_=，请你帮他解决这个问题，否则就把你吃掉变成他的魔法。为了拯救自己，赶紧想办法吧。

Input

输入包含多组，每组格式如下。

第一行包含两个整数n,m（分别代表n个隘口，这些隘口之间有m个通道）。

下面m行每行包含两个整数a，b；表示从a出发有一条通道到达b隘口（注意通道是单向的）。

Output

如果天灾军团可以不修建任何通道就到达1号隘口，那么输出最少经过多少通道，否则输出NO

#include <iostream> #include<cstring> #include<queue> using namespace std; const int maxn=1010; int G[maxn][maxn]; int vis[maxn]; int n,m; struct Node { int step; }; Node per[maxn];//存储步数！ bool sign; bool dfs(int a) { vis[a]=1; per[a].step=0; queue<int> num; num.push(a); while(!num.empty()) { int u=num.front(); num.pop(); for(int i=1;i<=n;i++) { if(G[u][i]&&i==1&&!vis[i]) { per[1].step=per[u].step+1; return true; } else if(G[u][i]&&!vis[i]) { num.push(i); vis[i]=1; per[i].step=per[u].step+1; } } } return false; } int main() { while(cin>>n>>m) { sign=false; memset(per,0,sizeof(per)); memset(G,0,sizeof(G)); memset(vis,0,sizeof(vis)); for(int i=0;i<m;i++) { int a,b; cin>>a>>b; G[a][b]=1; } if(dfs(n)) cout<<per[1].step<<endl; else cout<<"NO"<<endl; } return 0; } 

3.7 最短时间

（1）问题描述

Problem Description

X，作为户外运动的忠实爱好者，总是不想呆在家里。现在，他想把死宅Y从家里拉出来。问从X的家到Y的家的最短时间是多少。

为了简化问题，我们把地图抽象为n*m的矩阵，行编号从上到下为1 到 n，列编号从左到右为1 到 m。矩阵中’X’表示X所在的初始坐标，’Y’表示Y的位置 , ’#’表示当前位置不能走，’ * ’表示当前位置可以通行。X每次只能向上下左右的相邻的 ’*’ 移动，每移动一次耗时1秒。

Input

多组输入。每组测试数据首先输入两个整数n，m(1<= n ,m<=15 )表示地图大小。接下来的n 行，每行m个字符。保证输入数据合法。

Output

若X可以到达Y的家，输出最少时间，否则输出 -1。

Example

输出：4   -1

（2）题解代码

        使用结构体存储xy和该点最小步数，对二维坐标运用queue来进行BFS即可。

#include <iostream> #include<cstring> #include<cstdio> #include<string> #include<queue> using namespace std; char maps[16][16]; int vis[16][16]; int movex[]={-1,1,0,0}; int movey[]={0,0,-1,1}; int x1,y1,x2,y2,n,m; struct Node { int x,y,step; Node(int a,int b,int c):x(a),y(b),step(c) {} }; int dfs(int a,int b) { vis[a][b]=1; queue<Node> que; que.push(Node(a,b,0)); while(!que.empty()) { Node u=que.front(); que.pop(); for(int i=0;i<4;i++) { int dx=u.x+movex[i]; int dy=u.y+movey[i];//移动，相当于找图的联通部分 if(dx==x2&&dy==y2&&!vis[dx][dy])//目的地 { return u.step+1; } else if(dx>=1&&dx<=m&&dy>=1&&dy<=n&&!vis[dx][dy]&&maps[dx][dy]=='*')//否则继续走BFS { vis[dx][dy]=1; que.push(Node(dx,dy,u.step+1)); } } } return -1;//都没有则返回-1； } int main() { while(cin>>m>>n) { memset(maps,0,sizeof(maps)); memset(vis,0,sizeof(vis)); for(int i=1; i<=m; i++) { for(int j=1;j<=n;j++) { cin>>maps[i][j]; if(maps[i][j]=='X')//记录下起始位置和目的地位置 { x1=i;y1=j; } else if(maps[i][j]=='Y') { x2=i;y2=j; } } } int k=dfs(x1,y1); cout<<k<<endl; } return 0; } 

3.8 高楼电梯

Problem Description

有一座已知层数为n的高楼，这座高楼的特殊之处在于只能靠电梯去上下楼，所以要去到某一层要非常耽误时间，然而更悲哀的是，这座高楼的电梯是限号的，小鑫最开始的时候在1层，他想去第x层，问题是他最起码要经过多少层(包含第x层)才能到达第x层。

Input

Output

对于每次询问输出一个整数，占一行。代表如果要去某个楼层最少要经过多少层，如果到不了的话就输出-1。

#include <iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; int G[2001][2001]; int vis[2001]; int n,m,q,p; struct Node { int x; int step; Node(int aa,int bb):x(aa),step(bb) {} }; int BFS(int a) { vis[a]=1; queue<Node>que; que.push(Node(a,0));//对于1->1层问题，应该输出1，错在这里！原程序输出-1； while(!que.empty()) { Node u=que.front(); que.pop(); if(u.x==p) return u.step+1; for(int i=1;i<=n;i++) { //if(G[u.x][i]&&!vis[i]&&i==p)//原程序这样，若输入p=1的话，原本就在1层，1->1应为1但这里输出-1因为G[1][1]=0! //return u.step+1; if(G[u.x][i]&&!vis[i]) { que.push(Node(i,u.step+1)); vis[i]=1; } } } return -1; } int main() { while(cin>>n>>m>>q) { memset(G,0,sizeof(G)); for(int i=1;i<=m;i++) { int a,num,t; cin>>a>>num; for(int j=1;j<=num;j++) { cin>>t; G[a][t]=1; } } while(q--) { memset(vis,0,sizeof(vis)); cin>>p; int k=BFS(1); cout<<k<<endl; } } return 0; } 

3.9 PTA 喊山

（1）问题描述

Problem Description

一个山头呼喊的声音可以被临近的山头同时听到。题目假设每个山头最多有两个能听到它的临近山头。给定任意一个发出原始信号的山头，本题请你找出这个信号最远能传达到的地方。

Input
输入第一行给出3个正整数n、m和k，其中n（≤10000）是总的山头数（于是假设每个山头从1到n编号）。接下来的m行，每行给出2个不超过n的正整数，数字间用空格分开，分别代表可以听到彼此的两个山头的编号。这里保证每一对山头只被输入一次，不会有重复的关系输入。最后一行给出k（≤10）个不超过n的正整数，数字间用空格分开，代表需要查询的山头的编号。

Output

依次对于输入中的每个被查询的山头，在一行中输出其发出的呼喊能够连锁传达到的最远的那个山头。

注意：被输出的首先必须是被查询的个山头能连锁传到的。若这样的山头不只一个，则输出编号最小的那个。若此山头的呼喊无法传到任何其他山头，则输出0。

（2）题解代码

        对于数据n-10000建立邻接矩阵肯定不行了，那么我们只能用邻接表，但是指针很烦人。所以可以使用vector实现邻接表。

#include <iostream> #include<bits/stdc++.h> using namespace std; vector<int> line[10010];//用vector建立邻接表 bool vis[10010];//标记走过 int n,m,k; struct Node { int id; int step; Node(int a,int b):id(a),step(b) {} }; int BFS(int a) { if(line[a].empty()) return 0; vis[a]=1; int maxn=0; int dd=10001; queue<Node> que; que.push(Node(a,0)); while(!que.empty()) { Node u=que.front(); que.pop(); if(u.step>maxn)//判断 { dd=u.id; maxn=u.step; } else if(u.step==maxn) dd=dd<u.id?dd:u.id; for(int i=0; i<line[u.id].size(); i++) { if(!vis[line[u.id][i]]) { que.push(Node(line[u.id][i],u.step+1)); vis[line[u.id][i]]=1; } } } return dd; } int main() { cin>>n>>m>>k; while(m--) { int a,b; cin>>a>>b; line[a].push_back(b); line[b].push_back(a); } while(k--) { memset(vis,0,sizeof(vis)); int num; cin>>num; int mm=BFS(num); cout<<mm<<endl; } return 0; }