二叉搜索树（树表查找）

大家好，欢迎来到IT知识分享网。

目录

一、概念

1.二叉查找树 

 2.二叉查找树的查找

3.二叉查找树的插入

4.二叉查找树的创建

 5.二叉查找树的删除

二、代码

三、题目

1.Falling Leaves

2.BST

3.Hardwood Species

4.二叉搜索树

一、概念

1.二叉查找树 

二叉查找树，又称为二叉搜索树、二叉排序树，是一种对查找和排序都有用的特殊二叉树。

二叉查找树要么是空树，要么满足以下性质：

• 若其左子树非空，则左子树上所有结点的值均小于根节点的值；
• 若其右子树非空，则右子树上所有结点的值均大于等于根节点的值；
• 其左右子树本身又各是一棵二叉查找树。

左子树<根<右子树，即二叉查找树的中序遍历是一个严格递增序列

 2.二叉查找树的查找

因为二叉查找树的中序遍历有序，所以查找和二分查找类似，每次缩小查找范围，查找的效率较高。

算法步骤：

①若二叉查找树为空，查找失败，返回空指针；

②若二叉查找树非空，将带查找关键字x与根节点的关键字T->data比较：

• 若x==T->data，查找成功，返回根节点指针；
• 若x<T->data，则递归查找左子树；
• 若x>T->data，则递归查找右子树。

举例：

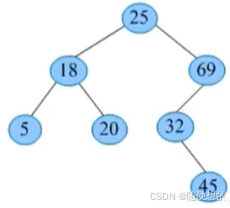
例如，一棵二叉查找树，查找关键字32。

 根节点25<32，从根节点的右子树查找；69>32，从69结点的左子树查找；32=32，找到关键字。

代码：

BSTree SearchBST(BSTree T,ElemType key){ if((!T) || key==T->data)//若查找成功，则返回指向该数据元素结点的指针，否则返回空指针 return T; else if(key<T->data){ SearchBST(T->lchild, key); } else{ SearchBST(T->rchild, key); } }

算法分析

二叉查找树的查找时间复杂度和树的形态有关（树高），可分为最好情况、最坏情况和平均情况分析。

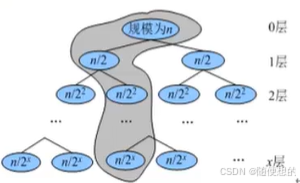
• 最好情况下，二叉查找树的形态和二分查找的判定树相似，如图所示。每次查找可以缩小一半的搜索范围，查找路径最多从根到叶子，比较次数最多为树的高度logn，最好情况的平均查找长度为O(logn)

  ​

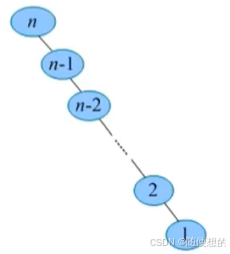
• 最坏情况下，二叉排序树的形态为单支树，即只有左子树或只有右子树，如图所示。每次查找的搜索范围缩小为n-1，退化为顺序查找，最坏情况的平均查找长度为O(n)。

3.二叉查找树的插入

首先要查找待插入关键字的插入位置，当查找不成功时，将待插入关键字作为新的叶子节点插入到最后一个查找结点的左孩子或右孩子。

算法步骤：

①若二叉查找树为空，创建一个新的结点s，将待插入关键字放入新结点的数据域，s结点作为根结点，左右子树均为空；

②若二叉查找树非空，将待查找关键字x与根结点的关键字T->data比较：

• 若x<T->data，则将x插入到左子树；
• 若x>T->data，则将x插入到右子树。

 举例：

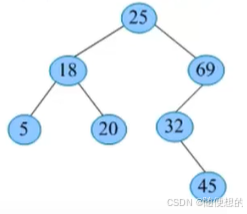
例如，一棵二叉查找树，插入关键字30

 根节点25<30，从根节点的右子树查找；69>30，从69结点的左子树查找；32>30，从32结点的左子树查找，左子树为空，查找不成功，创建一个新的结点插入为32结点的左节点。

若插入元素存在于二叉查找树中，那么查找成功时，怎么处理：①什么也不做返回；②每个结点增加一个域num=1，查找成功num++

代码： 

void InsertBST(BSTree &T,ElemType e){ //当二叉查找树T中不存在关键字等于e的数据元素时，则插入该元素 if(!T){ BSTree s=new BSTNode;//生成新结点 s->data=e; s->lchild=rchild=NULL; T=s; }//e==T->data不处理 else if(e<T->data){ InsertBST(T->lchild,e);//插入左子树 } else if(e>T->data){ InsertBST(T->rchild,e);//插入右子树 } }

 算法分析：

二叉查找树的插入需要先查找插入位置，插入本身只需常数时间，但查找插入位置的时间复杂度为O(logn)。

4.二叉查找树的创建

二叉查找树的创建从空树开始，按照输入关键字的顺序依次进行插入操作，最终得到一棵二叉查找树。

算法步骤：

①初始化二叉查找树为空树，T=NULL;

②输入一个关键字x，将x插入到二叉查找树T中；

③重复步骤②，直到关键字输入完毕。

代码：</