数据结构——查找

大家好，欢迎来到IT知识分享网。

查找

查找的概念

查找

在数据集合中寻找满足某种条件的数据元素的过程

查找表

用于查找的数据集合，可以是线性表、栈、队列、树、图等

查找表的操作

1. 查询某个特定的元素是否在查找表中
2. 检索满足条件的某个特定数据元素的各种属性
3. 在查找表中插入一个数据元素
4. 从查找表中删除某个数据元素

• 静态查找表：只有操作 1 和 2
• 动态查找表：包括 1 ~ 4

关键字

数据元素中唯一标识该元素的某个数据项的值。

平均查找长度（ASL, Average Search Length）——查找算法的评价指标

所有查找过程中进行关键字的比较次数的平均值

对 “每个元素被查找的概率 × 长度” 求和

• 注意查找二叉树查找失败时，需要画空的来计算。

顺序查找和折半查找

顺序查找

一般线性表的顺序查找

这里引入“哨兵”的概念

typedef struct SSTable { 
    // 查找表 ElemType *elem; // 元素存储空间基址，建表（用 malloc 或 new）时，0 号留空，放置“哨兵” int TableLen; }SSTable; int Search_Seq(SSTable ST, ElemType key) { 
    ST.elem[0] = key; // 放置“哨兵” for (int i = ST.TableLen; ST.elem[i] != key; i--); // 从表尾向表头扫描 return i; // 表中不存在 key 则返回 0，存在则返回位序 } 

引入“哨兵”，不必判断数组是否会越界。

ASL： 见 22 王道 P259

【注】若查找概率不等，能获知查找概率情况下，应按照查找概率排序（排序的规则取决于从表头开始还是从表尾开始查找）

有序表的顺序查找

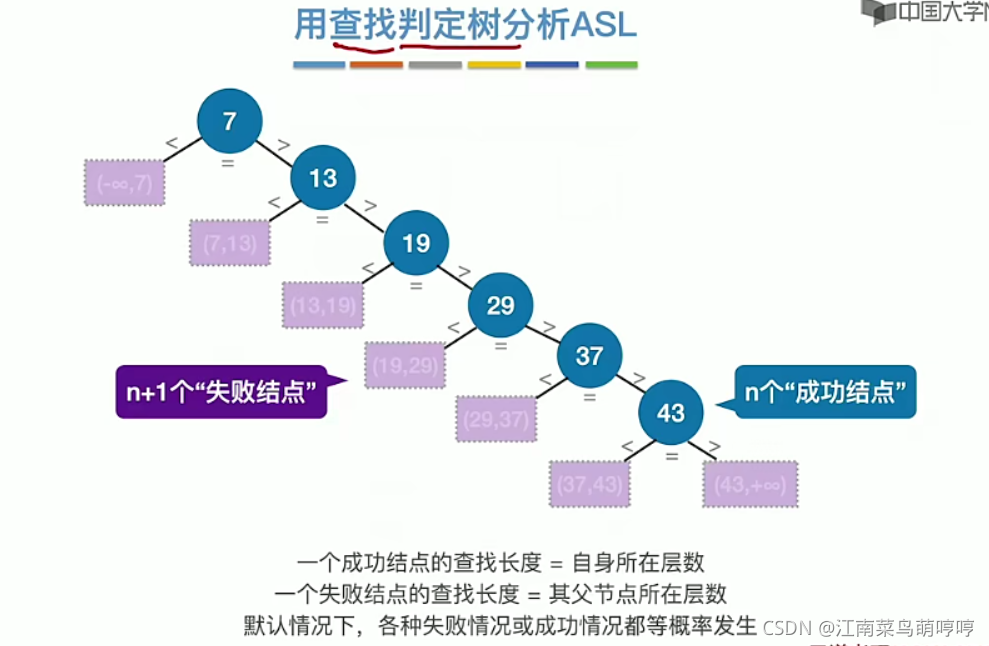
查找判定树

• 方形为查找失败结点
• 圆形为查找成功结点

🔸 计算查找失败 ASL

最好画出 查找判定树，本质是“插空”，在数据元素的左右“插空”，共会有 n + 1 个空，注意，查找“判定树”中最后一个数据元素失败时，有两个“空”，其长度都为 n 。

若查找概率不等，视具体情况分析：

• 如果将概率排序，查找成功的 ASL 将会优化，但查找失败无法得到优化。

折半查找——二分查找

仅适用于有序的顺序表，链表不适用（链表不能随机存取）

• 时间复杂度 log2(n)

算法思想

初始化 low、high、mid。

将给定 key 与表中间位置元素（下标为 mid）比较，有两种情况：

1. 相等；返回下标 mid
2. 不等，则 key 在左半区或右半区。

   key 在右：令 low = mid + 1；mid = (low + high) / 2; 再次查找

   key 在左：令 high = mid – 1；mid = (low + high) / 2; 再次查找

查找失败： low > high

// 设序列 L 是升序序列 int Binary_Search(SSTable L, ElemType key) { 
    int low = 0, high = L.Length - 1, mid = (low + high) /2; while (low <= high) { 
    mid = (low + high) / 2; // mid 取中间位置 if (L.elem[mid] == key) // 查找成功，返回下标 return mid; if (L.elem[mid] < key) // 如果 key 在 mid 右边 low = mid + 1; // low 变为 mid 后面一位 if (L.elem[mid] > key) // 如果 key 在 mid 左边 high = mid - 1; // high 变为 mid 前面一位 } return -1; // 跳出循环则说明 low > high ，查找失败！ } 

递归写法

int Binary_Sort(SSTable L, int low, int high, ElemType key) { 
    if (low <= high) { 
    mid = (low + high) / 2; if (L.elem[mid] == key) return mid; if (L.elem[mid] < key) Binary_Sort(L, low, mid - 1, key); if (L.elem[mid] > key) Binary_Sort(L, mid + 1, high, key); }else return -1; } 

🔸折半查找判定树

注意上述 mid 若改成向上取整，情况相反~

例子如下：

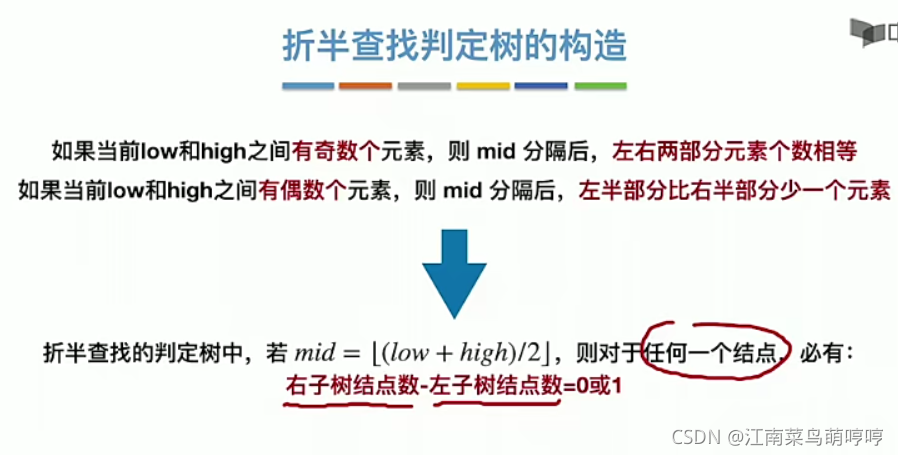
• 折半查找判定树是二叉排序树，每一颗子树的根结点是 每次折半查找时可能的 mid 结点。
• 对折半查找树进行 中序遍历 可得到正确排序。
• 对于查找失败的情况，在 二叉排序树 的 有空指针域 的结点的空指针域上连“方形结点”，表示查找失败的情况。
• 查找失败结点的个数 = 空指针域的个数 = n + 1

  也可以这么理解：在(-∞, +∞)上，对序列插空，有 n + 1 个位置可以插入，这些位置意味着查找失败。

• 折半查找判定树的树高，与完全二叉树的树高计算方式相同。

$$具有n个数据元素的查找表对应的折半查找二叉树高度h=\lceil {\log }_2(n+1)\rceil =\lfloor {\log }_{2}n\rfloor +1$$

分块查找——索引顺序查找

选择题中考得多

• 块内无序，块间有序。

数据结构

算法思想

0. 初始化一个 “索引表”：

typedef struct { 
    ElemType maxValue; // 记录块中最大值 int low, high; // 块的起始和终点下标 }Index; Index[BlockNum]; // 索引表 

1. 在索引表汇总确定待查记录所属的分块（可用 顺序查找、折半查找【块间有序】）
   • 若使用折半查找，有两种情况：

     ①：key = 索引表中的某个值，直接查找成功

     ②：key != 索引表中的某个值，此时需要找到 maxValue 恰好大于 key 的块

     但是由于是折半查找，如果 key != 索引表中任何一个值，最终都会导致 low > high，此时，注意一定是在 low 所指向的块 中继续顺序查找，但也要注意增加判断：如果 low 超过了索引，则查找失败。

2. 在对应的块内暴力顺序查找（块内无序）

ASL

一个数据元素的查找次数 = 第一步在索引表中查找次数 + 第二步在块内查找次数

每个数据元素按照上述方式计算，×其概率，求和即可。

查找效率分析

见 22 王道 P261-262

若均匀分块，块内长度一定，则可得到：

ASL = 索引查找平均长度 + 块内查找平均长度

存储结构优化

若查找表是“动态查找表”，可以采用在前面图一章中使用的“邻接表”来存储

瞎写的，仅供参考：

struct BlockNode { 
    // 这是一个块 ElemType maxValue; // 块内最大值 ElemInBlock *first; // 指向块内第一个元素 }; struct ElemInBlock { 
    ElemType value; // 块内一个元素 ElemInBlock *next; // 指向下一个块内元素 } struct LinkTable { 
    BlockNode[size] BlkNodes; int nodeNum; } 

B 树（Balanced Tree）与 B+ 树

多叉排序树

struct Node{ 
    ElemType keys[m - 1]; // 关键字最多 m - 1 个 Node *child[m]; // 一棵子树最多 m 叉，child 在 key 之间“插空” int keyNum; // 记录 key 的数目 }; 

• 根结点的 key 数目决定了子树的分叉树，结点中 key 的值按照升序或者降序排列，“插空”分叉，每个孩子拥有的 key 值都 ①介于双亲某两个 key 之间、 ②大于 双亲 key 中最大、③小于双亲 key 中最小。

• 每次查找都可以用 折半查找！

$$\begin{gathered} 规定：①除根结点外的所有非叶结点至少有\lceil m/2\rceil 棵子树，即至少含有\lceil m/2\rceil 个关键字。 \\ ②m叉树中，对于任一个结点，其子树高度都需要相同 \end{gathered}$$

B 树及其基本操作

B 树也叫做 多路平衡查找树，B 树中所有结点的孩子个数的最大值称为 B 树的阶，通常用 m 表示。

m 阶 B 树性质