六度空间理论实现

大家好，欢迎来到IT知识分享网。

目录

1 需求分析

1.1 任务

1.2 输入形式

1.3 输出形式

1.4 程序功能

2 概要设计

2.1 抽象数据类型

2.2 主程序流程图

3 详细设计

3.1 功能函数设计

3.2 主函数

4 调试分析

4.1 调试过程的问题

4.2 时空分析

4.3 经验体会

5 测试结果

5.1 数据输入

5.2 结果输出

1 需求分析

1.1 任务

        六度空间理论又称作“六度分隔”理论，其含义是：你和任何一个陌生人之间所建构的人不会超过6 个，即最多通过5 个人，你就能认识一个陌生人。假设有一个社交网络图，对每个结点计算符合六度空间理论的结点占结点总数的百分比。

1.2 输入形式

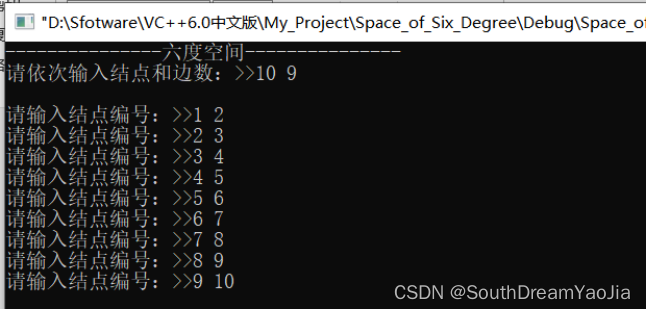
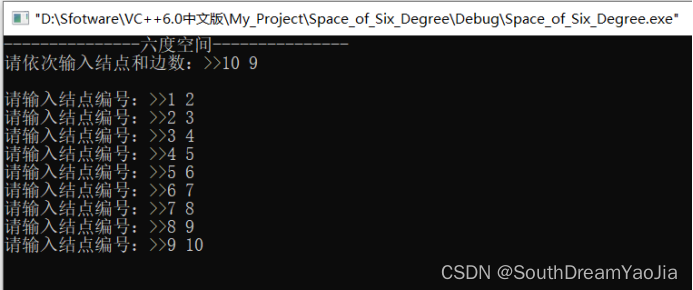
        输入第一行给出两个正整数，分别表示社交网络中的结点数 N（1<N<=10^3，表示人数）、边数 M（<=33*N，表示社交关系数）。随后的 M 行对应 M 条边，每行给出一对正整数，分别是该条边直接连通的两个结点的编号（结点从 1 到 N 编号）。

1.3 输出形式

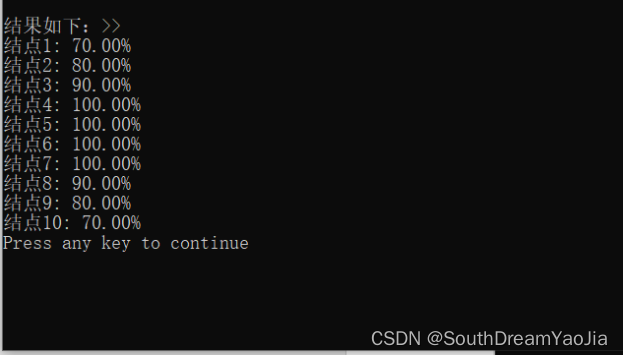
        对每个结点输出与该结点距离不超过 6 的结点数占总结点数的百分比，格式为“结点编号：百分比%”。

1.4 程序功能

        （1）构造图的邻接矩阵：“void BuildGraph()”根据输入的结点树和边数来初始化邻接矩阵，并根据后续输入结点构造邻接矩阵。

        （2）计算结点数目：“int BFS(int v)”计算与当前结点距离不超过 6 的结点数量。

        （3）计算结点比例：“void SDS()”根据“int BFS(int v)”的返回值和总结点数量计算与该结点距离不超过 6 的结点数占总结点数的百分比。

2 概要设计

2.1 抽象数据类型

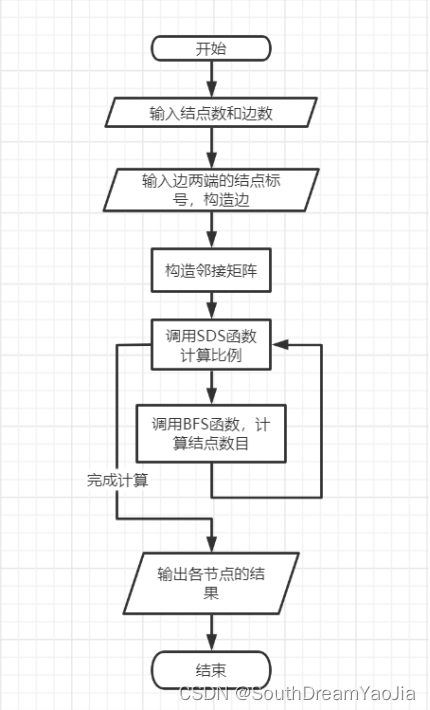
//定义图的存储结构：以邻接矩阵存储图的信息 int Graph[MAXN][MAXN]; //标记数组：用来标记某一结点是否已经被访问过 int visited[MAXN];

2.2 主程序流程图

3 详细设计

3.1 功能函数设计

//构造邻接矩阵： void BuildGraph(){ //创建邻接矩阵 int i,j,n1,n2; //初始化矩阵 for( i = 0; i < Nv; i++){ for( j = 0; j < Nv; j++){ Graph[i][j] = 0; } } //输入数值建立图 for(i = 0; i < Ne; i++){ printf("请输入结点编号：>>"); scanf("%d%d",&n1,&n2); Graph[n1][n2] = 1; Graph[n2][n1] = 1; } } //计算结点所占比例： void SDS(){ //计算比例 int i,j; float rate; for(i = 0; i < Nv; i++){ for(j = 0; j < Nv; j++)//初始化 visited[j] = 0; rate = (float)BFS(i) / Nv; printf("结点%d: %.2f%%\n",i+1,rate*100); } } //计算距离不超过 6 的结点数量： int BFS(int v){ //计算结点数目 int cnt = 1,level = 0, last = v,i,n,tail; int que[1000],rear,front;//模拟队列 rear = front =0; visited[v] = 1; que[rear] = v; rear++; while(rear > front){ n = que[front]; front++; for(i = 0; i < Nv; i++){ if(visited[i] == 0 && Graph[n+1][i+1] == 1){ visited[i] = 1; que[rear] = i; rear++; cnt++; tail = i; } } if(n == last){ level++; last = tail; } if(level == 6){ break; } } return cnt; }

3.2 主函数

int main(){ printf("---------------六度空间---------------\n"); printf("请依次输入结点和边数：>>"); scanf("%d%d",&Nv,&Ne); printf("\n"); BuildGraph(); printf("\n结果如下：>>\n"); SDS(); }

4 调试分析

4.1 调试过程的问题

        （1）问题1：最开始构建邻接矩阵的时候未初始化，致使程序出现问题。

                解决1：在构建邻接矩阵之前加入初始化的语句，保证邻接矩阵中未填入数据的部分的正确性。

        （2）问题2：在SDS函数中未对visited数组置“0”，导致后续函数调用出现问题。

                解决2：在SDS函数中加入对visited数组的置“0”操作，保证后续函数的正常使用。

4.2 时空分析

4.3 经验体会

        初始化和还原初始值的重要性：在程序的编写过程中一定要对数据进行基本的初始化，防止“类似野指针”的情况的出现，使得程序在后续执行中不确定。除此之外，还要注意对某些标记为的还原操作，在一次功能执行完之后，要对最基本的标记位进行还原操作，以供下一次执行使用

5 测试结果

5.1 数据输入

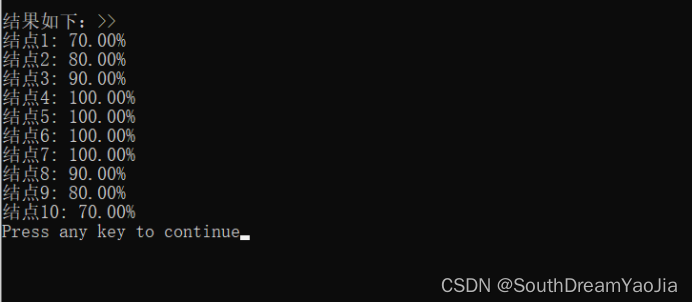
5.2 结果输出