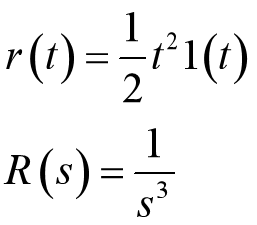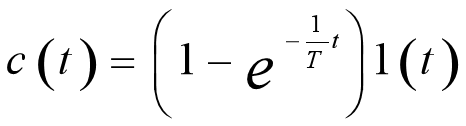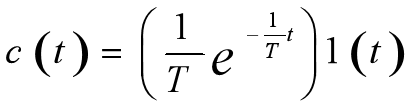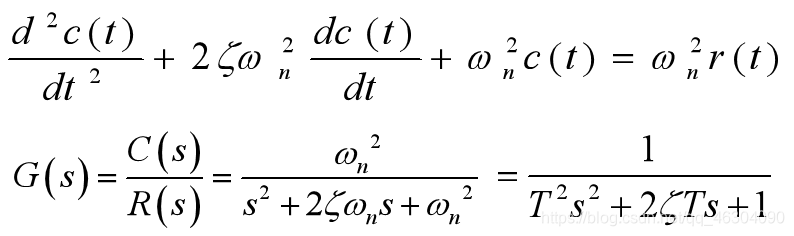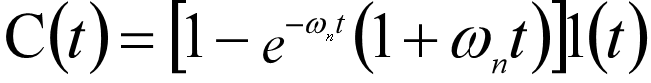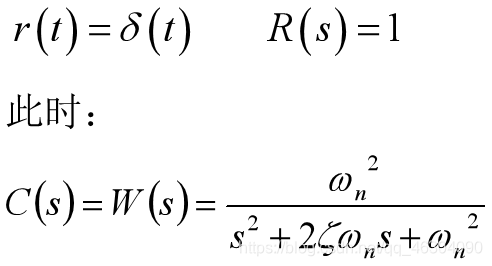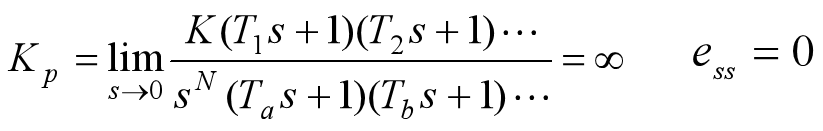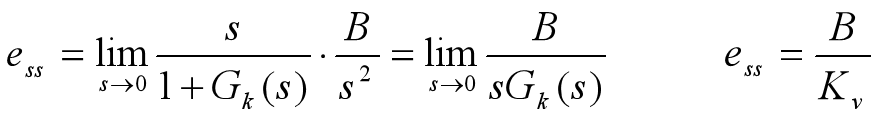大家好,欢迎来到IT知识分享网。
时域分析法
概述
控制系统性能分析方法
直接求解法、间接评价发、计算机仿真法
线性定常系统的主要性能指标
动态性能、稳定性、稳态误差
瞬态响应
系统在输入信号作用下,其输出量从初始状态到进入稳态之间随时间变化的过程。
典型输入信号
- 单位阶跃信号 (step function)
- 单位斜坡函数 (ramp function)
- 抛物线函数(parabolic function)
- 单位脉冲函数 (impulse function)
- 正弦函数(sine function)
动态性能指标
- 延迟时间 t d t_d td:指响应曲线第一次达到其终值一半的时间。
- 上升时间 t r t_r tr:指响应曲线从10%上升到其终值90%所需的时间;对于振荡系统指从零第一次上升到终值所需的时间。
- 峰值时间 t p t_p tp:指响应曲线超过其终值达到第一个峰值所需的时间。
- 调节时间 t s t_s ts:指响应响应到达并保持在终值5%内所需的时间。
- 超调量 σ \sigma σ%:指响应最大偏离量与终值之差与终值比的百分量。
一阶系统单位瞬态响应
一阶系统单位阶跃响应
一阶系统单位脉冲响应
二阶系统瞬态响应
二阶系统单位阶跃响应
- ζ > 1 \zeta>1 ζ>1
s 1 , 2 = − ζ ω n ± ω n ζ 2 − 1 s_{1,2}=-\zeta{\omega_n}\pm\omega_n\sqrt{\zeta^2-1} s1,2=−ζωn±ωnζ2−1
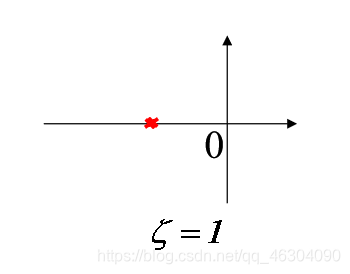
- ζ = 1 \zeta=1 ζ=1
s 1 , 2 = − ω n s_{1,2}=-\omega_n s1,2=−ωn
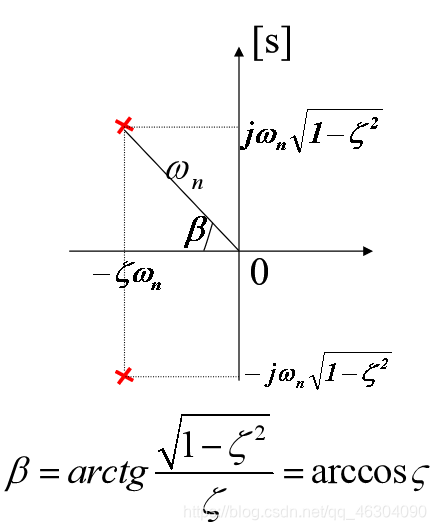
- 0 < ζ < 1 0<\zeta<1 0<ζ<1
s 1 , 2 = − ζ ω n ± j ω n 1 − ζ 2 s_{1,2}=-\zeta{\omega_n}\pm{j}\omega_n\sqrt{1-\zeta^2} s1,2=−ζωn±jωn1−ζ2
- ζ = 0 \zeta=0 ζ=0
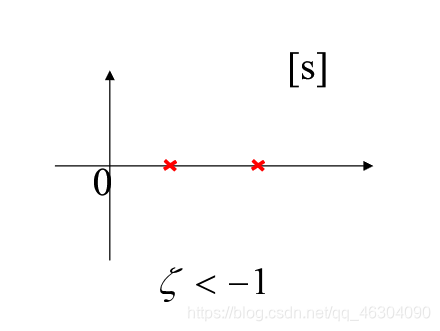
s 1 , 2 = ± j ω n s_{1,2}=\pm{j\omega_n} s1,2=±jωn - ζ < 0 \zeta<0 ζ<0
s 1 , 2 = − ζ ω n ± j ω n 1 − ζ 2 s_{1,2}=-\zeta{\omega_n}\pm{j}\omega_n\sqrt{1-\zeta^2} s1,2=−ζωn±jωn1−ζ2
负阻尼
(1)不相等的正实根
(2)共轭复根
二阶系统脉冲响应
- 0 < ζ < 1 0<\zeta<1 0<ζ<1
s 1 , 2 = − ζ ω n ± j ω n 1 − ζ 2 s_{1,2}=-\zeta{\omega_n}\pm{j}\omega_n\sqrt{1-\zeta^2} s1,2=−ζωn±jωn1−ζ2
- ζ = 1 \zeta=1 ζ=1
s 1 , 2 = − ω n s_{1,2}=-\omega_n s1,2=−ωn
欠阻尼二阶系统在阶跃输入作用下的瞬态响应指标
- 上升时间
- 峰值时间
- 最大超调量
- 调整时间
参数对系统的影响
欠阻尼二阶系统瞬态响应性能完全取决于阻尼比 ζ \zeta ζ和无阻尼自然振荡频率 ω n \omega_n ωn。
(1)当ωn一定,要减小tr和tp,必须减少ζ 值,要减少ts则应增大ζ、 ωn 值,而且ζ 值有一定范围,不能过大。
(2)增大ωn ,能使tr,tp和ts都减少。
(3)最大超调量σp只由ζ 决定,ζ 越小,σp越大。所以,一般根据σp的要求选择ζ值,在实际系统中,ζ值一般在0.5-0.8之间。而对各种时间性能指标的要求,则可通过ωn的选取来满足 。
改善二阶系统性能的措施
线性定常系统的特性
- 当线性定常系统输入信号为原来输入信号的导数时,这时系统的输出也为原来输出的导数。
- 在零初始条件下,当线性定常系统输入信号为原来输入信号对时间的积分时,则系统的输出为原来输出的积分。
- 由于单位脉冲信号是单位阶跃信号对时间的一阶导数,所以单位脉冲响应也是单位阶跃响应对时间的一阶导数。
- 由于单位斜坡信号和单位抛物线信号分别是单位阶跃信号对时间的一重和二重积分,所以单位斜坡响应和单位抛物线响应也应是单位阶跃响应对时间的一重和二重积分。
零极点的性质
- 闭环传递函数中,如果零、极点数值上相近,则可将该零点和极点一起消去,称之为偶极子相消。
- 系统极点的负实部愈是远离虚轴,则该极点对应的项在瞬态响应中衰减得愈快。反之,距虚轴最近的闭环极点对应着瞬态响应中 衰减最慢的项,该极点对(或极点)对瞬态响应起主导作用,称之为主导极点。 工程上当极点A距虚轴的距离大于5倍的极点B距虚轴的距离时,分析时可忽略极点A。
- 找到了一对共轭复数主导极点,高阶系统就可以近似地当作二阶系统来分析,相应的性能指标都可以按二阶系统进行近似估计。
稳定性
基本概念
线性系统稳定的充要条件
系统特征方程式的根全部具有负实部。或说闭环传递函数的极点全部具有负实部(位于左半s平面)。
劳斯判据
系统稳定性的初步判别
劳斯判据
- 要求a0>0。
- 稳定的充分条件:劳斯阵列中第一列所有项>0 。
特殊情况
- 某一行第一个元素为零,而其余各元素均不为零、或部分不为零;
此时将这个0用 ε \varepsilon ε代替。 ε \varepsilon ε极限趋近于0,下一行用 ε \varepsilon ε代入计算,根据极限的正负判断是否稳定。 - 某一行所有元素均为零
系统必然存在关于坐标原点为对称的根。即存在等值反号的实根 、共轭虚根或偶数对共轭复根。系统必然非渐进稳定。
解决方法:
(1)构成辅助多项式,并求导,用其系数代替全为零的行;
(2)构成辅助方程,并解出这些大小相等但位置径向相反的特征根。
例:
应用
- 稳定裕量的检验
- 分析系统参数对稳定性的影响
赫尔维茨判据
稳态误差分析
系统分类
阶跃输入作用下的稳态误差计算(r(t)=A﹒1(t))
0型系统
Ⅰ型及Ⅰ型以上系统
斜坡输入作用下的稳态误差计算(r(t)=B﹒t)
静态速度误差系数:
0型系统
Ⅰ型系统
Ⅱ型及Ⅱ型以上系统
抛物线函数输入作用下的稳态误差计算( r ( t ) = 1 / 2 C ∗ t 2 r(t)= 1/2C*t^2 r(t)=1/2C∗t2)
加速度误差系数:
0 型系统
Ⅰ型系统
Ⅱ型系统
Ⅱ型以上系统
主扰动输入引起的稳态误差
降低稳态误差的主要措施
- 保证元件有一定的精度和性能稳定性,尤其是反馈通道元件。有时还应考虑实际的环境条件,采取必要的误差补偿等措施。
- 在满足系统稳定性要求的前提下,增大系统开环放大系数或增加前向通道中积分环节数目,保证对参考输入的跟随能力;增大扰动作用点之前的前向通道放大系数或增加扰动作用点之前的前向通道的积分环节数,以降低扰动引起的稳态误差。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/120877.html