【概率方法】MCMC

大家好，欢迎来到IT知识分享网。

纯天然无污染博文，请放心食用 

什么是 MCMC？

MCMC 是 Markov Chain Monte Carlo （马尔科夫链蒙特卡洛），是一种采样方法。

接受-拒绝采样的缺点

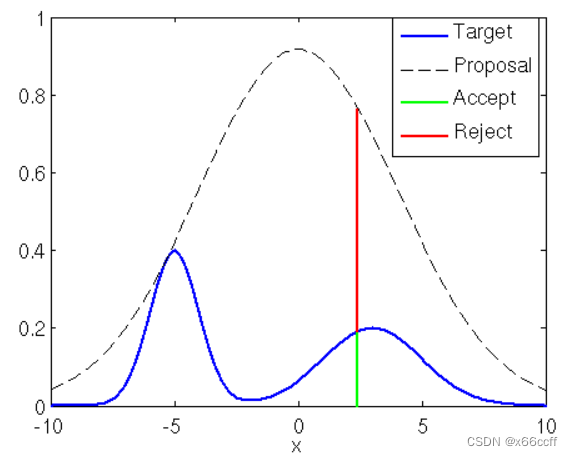
要从一个复杂分布 $p(x)$ 里面采样，并且这个分布可以计算给定 $x$ 的概率（或者未归一化概率 $\tilde{p}(x)$，即 $p(x)=\frac{\tilde{p}(x)}{{\sum }_x\tilde{p}(x)}$），可以使用接受-拒绝采样（ Acceptance-Rejection Sampling）：

• 需要选择一个简单分布 $q(x)$（满足1. 容易算概率 2.容易采样），并且选择系数 $k,\forall xkq(x)>p(x)$。 每一次先从 $q(x)$ 采样一个 $x$，再采样一个 $u\sim U(0,1)$ 如果 $u<\frac{p(x)}{kq(x)}$ 就接受这个采样结果，否则拒绝。

但是，接受-拒绝采样的问题至少有两点：

• 两个分布（的形状）过于不匹配的时候，$k$ 需要很大才能满足条件，造成采样效率很低
• 高维情况下，即使两个分布（的形状）匹配，但是由于每一个维度$q(x)$ 都要大一点，综合考虑所有维度时，实际还是造成采样效率低

因此，需要新的采样算法

MCMC 的基本思想

• 不要从头采样：在拒绝采样中，可以发现，每一次采样都是独立的。新的采样并没有利用老的采样。如果我们可以基于上一次采样的结果$x_t$ ，来采样出新的样本$x_{t+1}$，而不是从头开始采样，那么效率有可能提高。
• 建模成马尔科夫链的稳态：
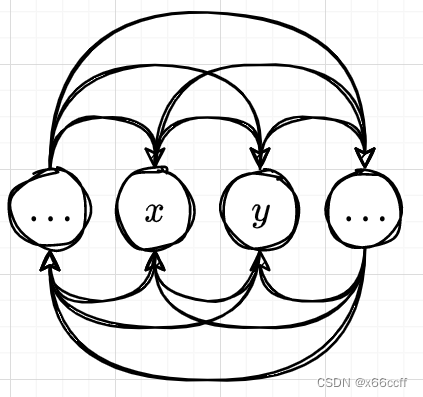
  • 由于新状态仅仅取决于上一个状态，所以很显然满足马尔可夫性，因此我们可以用马尔可夫链进行建模。
  • 我们把每一个状态 $x$ 当作一个分布，如果要满足我们上一次采样$x_t$和这一次采样$x_{t+1}$ 的分布都是相同的，那么说明这个马尔科夫链达到了稳态。我们可以选择它的一个充分条件——细致平衡（Detailed Balance）：
    $${\pi }_i{P}_{ij}={\pi }_j{P}_{ji}\forall i,j$$
    也可以写成
    $$p(x)T(y|x)=p(y)T(x|y)\forall x,y$$
    它表示各个状态之间的边上的“流”达到平衡，那么整个图自然是平衡的，也就是说马尔科夫链达到稳态。
    
    
    
    

也就是说，如果我们能够设计一个这样的算法，它能够从某个非稳态$x_0$开始，逐渐利用前一个采样出来的样本$x_t$，采样下一个样本$x_{t+1}$，并且满足细致平衡条件： $p(x)T(y|x)=p(y)T(x|y)\forall x,y$ ，那么我们就能够对 $p(x)$ 进行采样

如何设计这样的一个算法呢？

Metropolis – Hastings 算法

假设我们要采样一个「可以算给定 $x$ 的概率，但是难以用接受-拒绝采样进行采样的分布 $p(x)$」
首先选择一个简单分布（可以是正态分布），然后构造满足对称性（$g(x|y)=g(y|x)\forall x,y$）的 $g(x_{t+1}|x_t)=N(x_t,{\sigma }^2)$，$\sigma$ 自定义。 这表示我们采样下一个样本的时候，是根据前一个采样出来的被接受的样本 $x_t$ ，作为正态分布的均值，然后采样下一个提议的样本 。

每给出一个提议的样本 $x_{t+1}$ ，我们计算接受概率（取 min 1 是因为概率不能超过1）：
α ( x t + 1 , x t ) = min ⁡ { p ( x t + 1 ) p ( x t ) , 1 } \alpha(x_{t+1},x_t)=\min\{ \frac{p(x_{t+1})}{p(x_{t})},1\} α(xt+1​,xt​)=min{
p(xt​)p(xt+1​)​,1}

然后 random 一个均匀分布随机数出来 $u\sim U(0,1)$，如果$u<\alpha$ ，那么就接受这个提议的样本 $x_{t+1}$ ，否则，重新从 $g$ 里面采样。

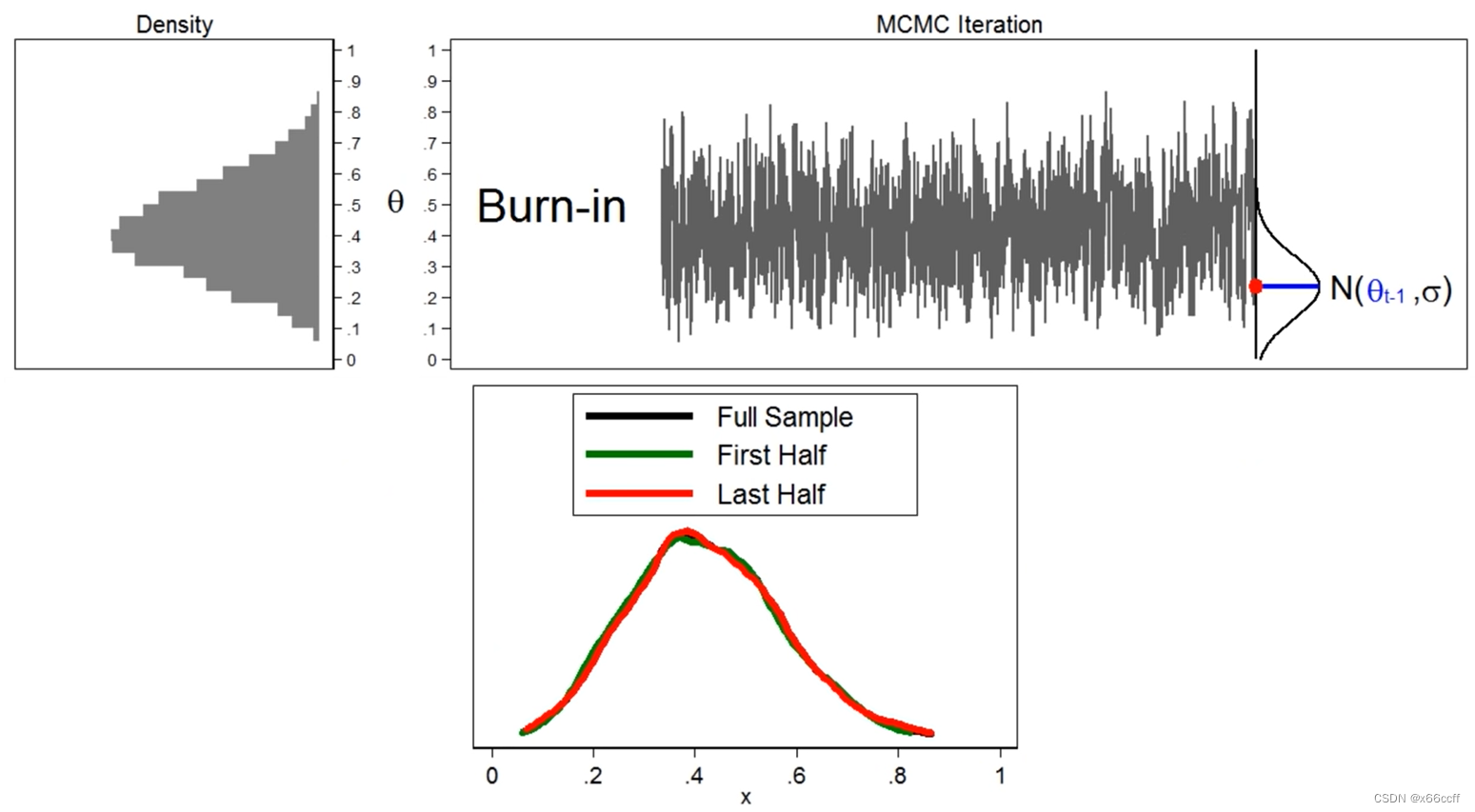
从随便一个 $x_0$ 出发，重复上述采样步骤，当步数足够多的时候，比如说超过我们设定的超参$B$ （称为 Burn-in step，不妨译为煲机冷启动步数），我们就认为分布已经达到稳态了，此时采样出来的分布就是我们想要的 $p(x)$

为什么有用？

只需要证明满足前面说的细致平衡条件 $p(x)T(y|x)=p(y)T(x|y)$ 就可以了。

• 当 $x=y$，显然满足
• 当 $x\ne y$， p ( x ) T ( y ∣ x ) ⏞ 转移概率 = p ( x ) g ( y ∣ x ) ⏞ 提议概率 α ( x , y ) ⏞ 接受概率 = p ( x ) g ( y ∣ x ) min ⁡ { p ( y ) p ( x ) , 1 } = g ( y ∣ x ) min ⁡ { p ( y ) , p ( x ) } = min ⁡ { p ( y ) g ( y ∣ x ) , p ( x ) g ( y ∣ x ) } = min ⁡ { p ( y ) g ( x ∣ y ) , p ( x ) g ( y ∣ x ) } p(x)\overbrace{T(y|x)}^{转移概率} =p(x) \overbrace{g(y|x)}^{提议概率}\overbrace{ \alpha(x,y)}^{接受概率} = p(x)g(y|x)\min\{ \frac{p(y)}{p(x)},1\}=g(y|x)\min\{p(y),p(x)\}=\min\{p(y)g(y|x),p(x)g(y|x)\}=\min\{p(y)g(x|y),p(x)g(y|x)\} p(x)T(y∣x)
  
  
  ​转移概率​=p(x)g(y∣x)
  
  
  ​提议概率​α(x,y)
  
  
  ​接受概率​=p(x)g(y∣x)min{
  p(x)p(y)​,1}=g(y∣x)min{
  p(y),p(x)}=min{
  p(y)g(y∣x),p(x)g(y∣x)}=min{
  p(y)g(x∣y),p(x)g(y∣x)}
  同理 p ( y ) T ( x ∣ y ) = min ⁡ { p ( y ) g ( x ∣ y ) , p ( x ) g ( y ∣ x ) } p(y)T(x|y)=\min\{p(y)g(x|y),p(x)g(y|x)\} p(y)T(x∣y)=min{
  p(y)g(x∣y),p(x)g(y∣x)} ，因此 $p(x)T(y|x)=p(y)T(x|y)$
  

综上，MH 算法步数足够多的时候满足细致平衡条件。

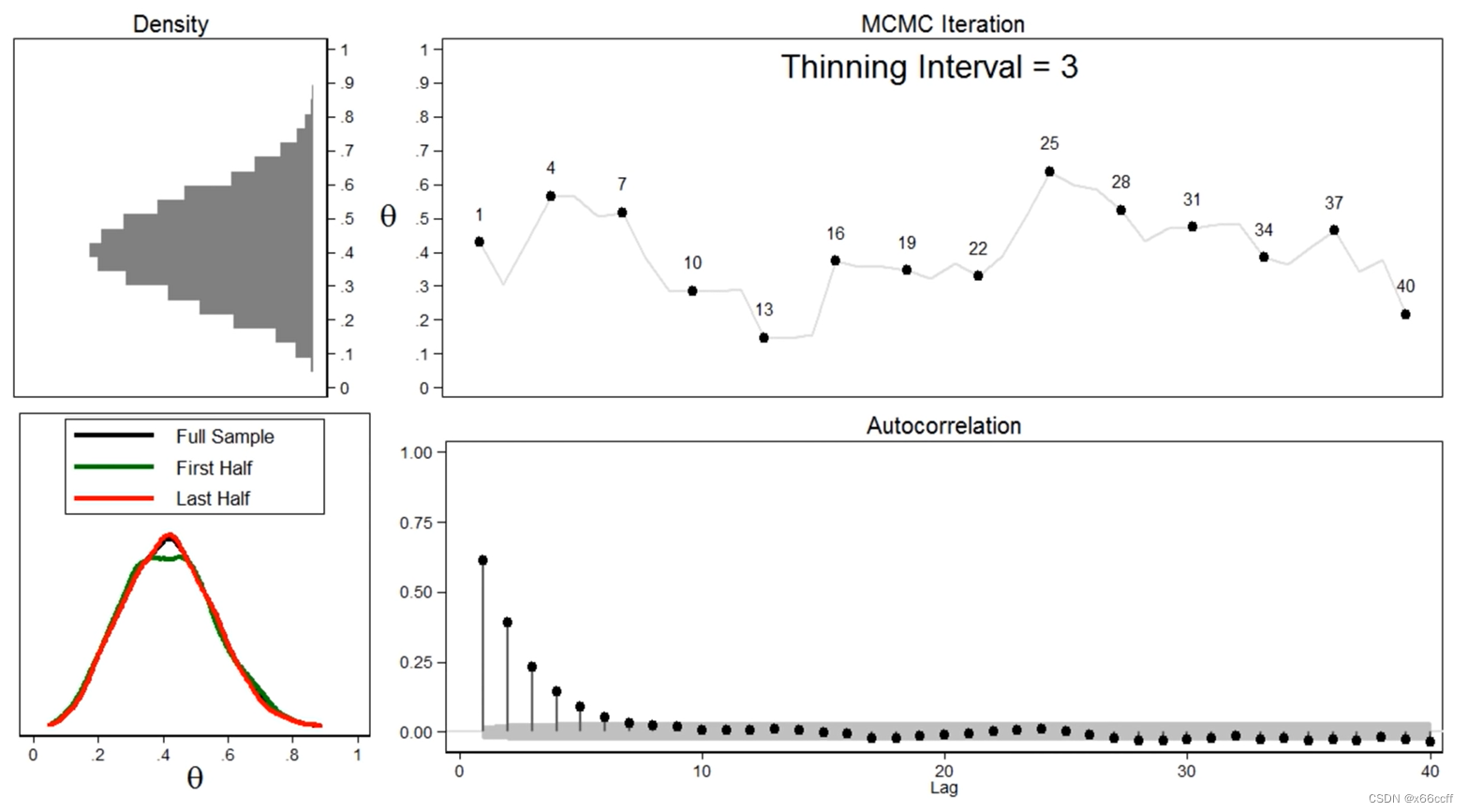
Thinning

代码

 samples = [1] num_accept = 0 for _ in range(N): #sample candidate from normal distribution candidate = np.random.normal(samples[-1], 4) #calculate probability of accepting this candidate prob = min(1, f(candidate) / f(samples[-1])) #accept with the calculated probability if np.random.random() < prob: samples.append(candidate) num_accept += 1 #otherwise report current sample again else: samples.append(samples[-1]) 

burn_in = 1000 retained_samples = samples[burn_in+1:] 

print("Num Samples Collected: %s"%len(retained_samples)) 

Num Samples Collected:

print("Efficiency: %s"%round(len(retained_samples) / N, 3)) 

Efficiency: 0.999

 print("Fraction Acceptances: %s"%(num_accept / N)) 

Fraction Acceptances: 0.

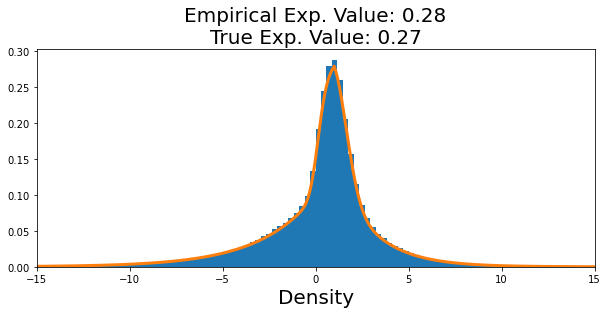
 plt.figure(figsize=(10,4)) plt.hist(retained_samples, bins=200, density=True) plt.xlabel('x', fontsize=20) plt.xlabel('Density', fontsize=20) plt.plot(x_vals, [f/NORM_CONST for f in f_vals], linewidth=3) plt.xlim(-15,15) plt.title('Empirical Exp. Value: %s\nTrue Exp. Value: %s'%(round(np.mean(retained_samples), 2), round(np.mean(TRUE_EXP), 2)), fontsize=20)