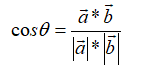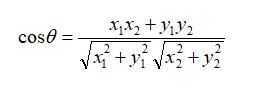十种距离计算公式及Python简单实践（余弦距离、欧式距离、jaccard距离等）

大家好，欢迎来到IT知识分享网。

一、余弦距离

形式化描述：

余弦夹角也可以叫余弦相似度。几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。

余弦取值范围为[-1,1]。求得两个向量的夹角，并得出夹角对应的余弦值，此余弦值就可以用来表征这两个向量的相似性。夹角越小，趋近于0度，余弦值越接近于1，它们的方向更加吻合，则越相似。当两个向量的方向完全相反时，夹角余弦取最小值-1。当余弦值为0时，两向量正交，夹角为90度。因此可以看出，余弦相似度与向量的幅值无关，只与向量的方向有关。

公式描述：

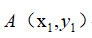
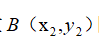
在二维空间中向量与向量的夹角余弦公式为：

Python实现：

import numpy as np vec1 = [1,2,3,4] vec2 = [5,6,7,8] #法一：根据公式求解 dist1 = np.dot(vec1,vec2)/(np.linalg.norm(vec1)*np.linalg.norm(vec2)) print("余弦距离为：\t"+str(dist1)) #法二：根据scipy库求解 from scipy.spatial.distance import pdist Vec = np.vstack([vec1,vec2]) dist2 = 1 - pdist(Vec,'cosine') print("余弦距离为：\t"+str(dist2))

余弦距离为： 0.69662 余弦距离为： [0.]

二、欧式距离

形式化描述：

在数学中，欧几里德距离或欧几里德度量是欧几里德空间中两点间“普通”（即直线）距离。使用这个距离。欧式空间成为度量空间。相关联的范数称为欧几里德范数。较早德文献称之为毕达哥拉斯度量。

公式化描述：

1）平面上两点

三、曼哈顿距离

四、明可夫斯基距离

五、切比雪夫距离

六、杰卡德距离

七、汉明距离

八、标准化欧式距离

九、皮尔逊相关系数

十、编辑距离

来源：自然语言处理理论与实战