十大排序——堆排序

大家好，欢迎来到IT知识分享网。

之前我们了解了堆，堆一个重要的应用就是堆排序，如果对堆的概念还不是很了解的可以点击这里：

十大排序——堆排序

堆排序

堆排序是一种基于比较的排序算法，它利用了完全二叉树特性的堆数据结构来进行排序。堆排序的基本思想是将待排序序列构建成一个大顶堆（对于升序排序）或小顶堆（对于降序排序），然后通过反复交换堆顶元素与末尾元素并重新调整堆，最终使得整个序列有序。以下是对堆排序的详细步骤说明：

步骤一：构建堆

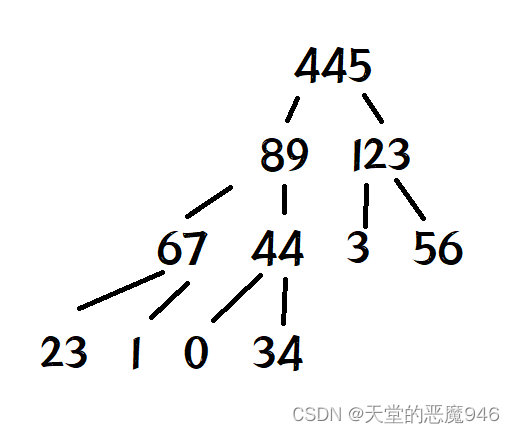
1. 初始化堆：对待排序序列进行初步处理，将其视为一个完全二叉树的层次序列表示，并将该树调整为大顶堆或小顶堆。通常从最后一个非叶子节点开始，自底向上逐个进行向下调整操作（Sift Down），确保每个子树都满足堆的性质。

• 大顶堆：父节点的值大于或等于其子节点的值，堆顶元素是当前最大值。
• 小顶堆：父节点的值小于或等于其子节点的值，堆顶元素是当前最小值。

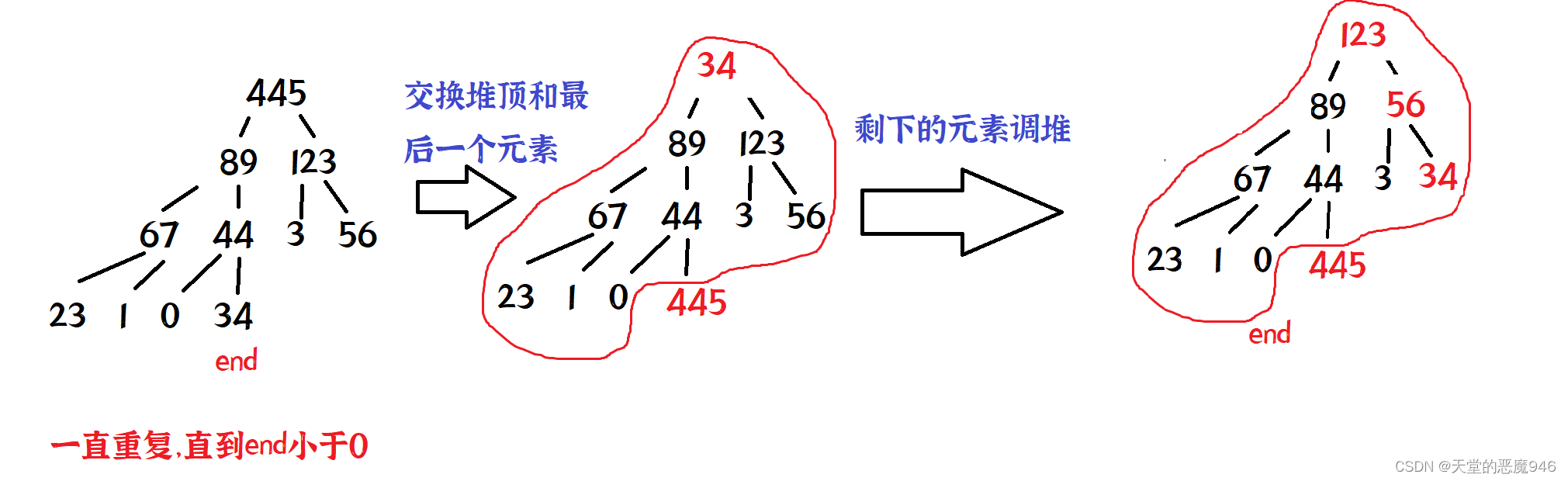
步骤二：交换堆顶元素与末尾元素

1. 交换堆顶元素与最后一个元素：将堆顶元素（最大值或最小值）与序列末尾元素交换位置。这一步骤将最大（小）值“沉”到底部，同时保证了剩余元素组成的子序列仍满足堆的性质。

步骤三：调整堆

1. 调整剩余元素：将交换后剩下的元素（除去已排序的堆顶元素）重新调整为一个堆。由于堆顶元素已被移到末尾，此时需要对剩余元素重新执行向下调整操作，使得新的堆顶元素成为剩余元素中的最大（小）值。

步骤四：重复步骤二和步骤三

1. 重复交换与调整：重复步骤二和步骤三，每次都将当前堆顶元素（即剩余部分的最大或最小值）与末尾元素交换，并对剩余元素重新调整为堆。随着每一次交换和调整，有序序列逐渐扩大，堆的大小逐渐减小。

2. 终止条件：当堆的大小减小到1时，整个序列已经有序，堆排序过程结束。

时间复杂度与空间复杂度

• 时间复杂度：构建堆的时间复杂度为 O(n)，因为需要对 n 个元素进行一次向下调整操作。交换堆顶元素与末尾元素并重新调整堆的过程需要重复 n-1 次，每次调整的时间复杂度为 O(log n)。因此，总的时间复杂度为 O(n log n)。
• 空间复杂度：堆排序是原地排序算法，只需要一个额外的空间存储临时变量（如交换元素时的暂存），所以空间复杂度为 O(1)。

特点与应用场景

• 稳定性：堆排序不是稳定的排序算法，因为相等的元素可能会因为交换操作而改变它们在原序列中的相对顺序。
• 适用场景：堆排序适用于大规模数据的排序，尤其是当内存不足以容纳全部待排序数据，需要在外部存储设备（如硬盘）上进行排序时。由于堆排序不需要额外的存储空间，且时间复杂度较低，因此在这些场景中具有较高的实用价值。

总之，堆排序是一种基于完全二叉堆的高效排序算法，通过构建、交换和调整堆的系列操作，实现对序列的升序或降序排序。尽管不是稳定的排序算法，但由于其原地性和较好的平均时间复杂度，适用于对大规模数据进行排序的场景。

升降序问题

现在有一个问题，如果我们想数据升序，是建大根堆还是小根堆呢？

我们会发现如果是小根堆来排升序的数据，会极大的破坏堆的关系结构。
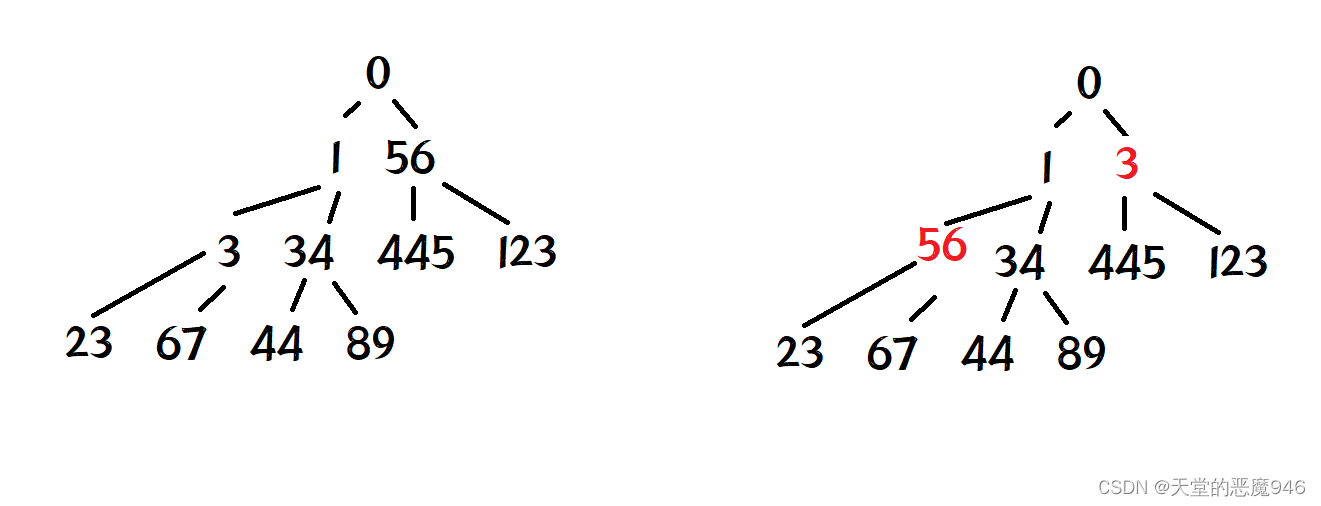
那么如果我们想排升序，是要排大根堆吗？

答案是——是的。

step1：堆顶和最后一个元素交换。
step2：将剩下的元素重新调整。
step3：下标减一。

这里我们就用向下调整算法举例，向上调整算法的例子大家可以自己尝试：

#pragma once #include<iostream> #include<vector> // 堆类模板定义 template<class T> class Heap { 
    public: // 默认构造函数，初始化大小为0，容量为10的堆 Heap() :_size(0) { 
    _data.resize(10); } // 带参数的构造函数，根据输入的size初始化堆的大小和容量 Heap(const size_t& size) :_size(0) { 
    _data.resize(size); } // 插入元素data到堆中 void insert(const T& data) { 
    // 如果堆已满，则将容量扩展到原来的两倍 if(_size >= _data.capacity()) { 
    _data.resize(2 * _size); _capacity = _data.capacity(); } // 将新元素插入到堆尾，并更新堆的大小 _data[_size++] = data; } // 向下调整算法（最小堆），从索引index开始调整 void AdjustDown_to_Min(size_t index,size_t size) { 
    // 计算左孩子的索引 size_t child = 2 * index + 1; // 当左孩子存在时执行循环 while(child< size) { 
    // 确定较小的子节点 if(child + 1< size && _data[child] > _data[child+1]) { 
    child++; } // 如果当前节点小于等于较小的子节点，则不需要调整，跳出循环 if(_data[index] <= _data[child]) break; // 交换当前节点与较小子节点的值 std::swap(_data[index],_data[child]); // 更新索引和左孩子的索引，继续循环 index = child; child = 2 * index + 1; } } // 向下调整算法（最大堆），从索引index开始调整 void AdjustDown_to_Max(size_t index,size_t size) { 
    // 计算左孩子的索引 size_t child = 2 * index + 1; // 当左孩子存在时执行循环 while(child< size) { 
    // 确定较大的子节点 if(child + 1< size && _data[child] < _data[child+1]) { 
    child++; } // 如果当前节点大于等于较大的子节点，则不需要调整，跳出循环 if(_data[index] >= _data[child]) break; // 交换当前节点与较大子节点的值 std::swap(_data[index],_data[child]); // 更新索引和左孩子的索引，继续循环 index = child; child = 2 * index + 1; } } // 堆排序（升序），构建一个最小堆，然后将堆顶元素依次与尾部元素交换并调整堆 void HeapSort_increase() { 
    // 从最后一个非叶子节点开始，构建最小堆 for(int i = (_size - 1 - 1)/2; i >= 0; i--) { 
    AdjustDown_to_Max(i,_size); } // 将堆顶元素依次与尾部元素交换，并从堆中删除已排序的元素 int end = _size - 1; while (end > 0) { 
    std::swap(_data[0], _data[end]); AdjustDown_to_Max(0,end); end--; } } // 堆排序（降序），构建一个最大堆，然后将堆顶元素依次与尾部元素交换并调整堆 void HeapSort_decrease() { 
    // 从最后一个非叶子节点开始，构建最大堆 for(int i = (_size - 1 - 1)/2; i >= 0; i--) { 
    AdjustDown_to_Min(i,_size); } // 将堆顶元素依次与尾部元素交换，并从堆中删除已排序的元素 int end = _size - 1; while (end > 0) { 
    std::swap(_data[0], _data[end]); AdjustDown_to_Min(0,end); end--; } } // 返回堆中元素的个数 size_t size() { 
    return _size; } // 返回堆的容量 size_t capacity() { 
    return _capacity; } // 打印堆中的所有元素 void printHeap() { 
    for(int i = 0; i < _size; i++) { 
    std::cout << _data[i] << " "; } std::cout<< std::endl; } private: std::vector<T> _data; // 使用vector存储堆中的元素 size_t _size; // 记录堆中元素的个数 size_t _capacity; // 记录堆的容量 }; 

//#include"HeapSort.h" //#include"HeapSort2.h" #include"HeapSort3.h" int main() { 
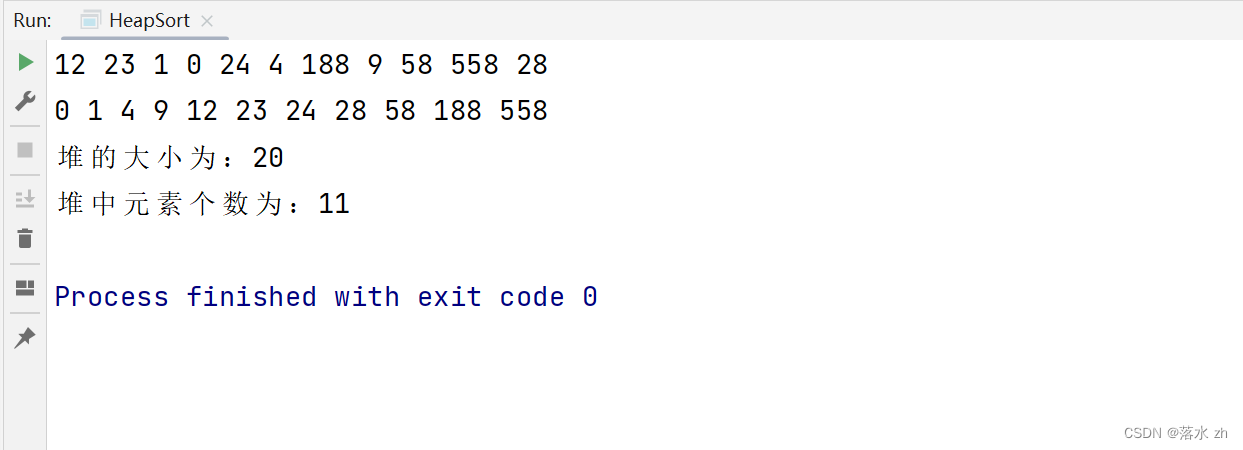
    Heap<int> heap; //用向下调整算法建立小根堆 heap.insert(12); heap.insert(23); heap.insert(1); heap.insert(0); heap.insert(24); heap.insert(4); heap.insert(188); heap.insert(9); heap.insert(58); heap.insert(558); heap.insert(28); heap.printHeap(); heap.HeapSort_decrease(); heap.printHeap(); std::cout << "堆的大小为：" << heap.capacity() << std::endl; std::cout << "堆中元素个数为：" << heap.size() << std::endl; return 0; } 

升序：

//#include"HeapSort.h" //#include"HeapSort2.h" #include"HeapSort3.h" int main() { 
    Heap<int> heap; //用向下调整算法建立小根堆 heap.insert(12); heap.insert(23); heap.insert(1); heap.insert(0); heap.insert(24); heap.insert(4); heap.insert(188); heap.insert(9); heap.insert(58); heap.insert(558); heap.insert(28); heap.printHeap(); heap.HeapSort_increase(); heap.printHeap(); std::cout << "堆的大小为：" << heap.capacity() << std::endl; std::cout << "堆中元素个数为：" << heap.size() << std::endl; return 0; } 

TOK问题

Topk问题研究的的是：在海量的数据中选取最大或最小的K个数。
比如说：

1. 在一亿的玩家中选出积分排名前五的玩家信息。
2. 选出全中国评分最高的五家店铺

套用模板的话就是：在N个数据中选取最XX的K个数据。
步骤为：

step1：以数据中的前K个数建堆。(最大数建小堆，最小数建大堆)
step2：将剩下的N-K的数依次和堆顶的数据比较，满足条件就覆盖原来的堆顶。
step3：完成上述步骤后进行调堆。

// TopKSelect_Min 函数用于找到数组中最小的前 N 个元素 void TopKSelect_Min(int N, int K) { 
    // 创建一个大小为 N 的最小堆 Heap<T> vt(N); // 将前 N 个元素插入堆中 for(int i = 0; i < N; i++) { 
    vt.insert(_data[i]); } // 调整堆结构，使其满足最小堆的性质 for(int i = (N - 1 - 1)/2; i >= 0; i--) { 
    vt.AdjustDown_to_Max(i,N); } // 遍历剩余的 K-N 个元素 for (int i = N; i < K; i++) { 
    // 如果当前元素小于堆顶元素，则替换堆顶元素 if (vt._data[0] > _data[i]) { 
    vt._data[0] = _data[i]; } // 调整堆结构，使其满足最小堆的性质 vt.AdjustDown_to_Max(0,N); } // 打印最小堆 vt.printHeap(); } // TopKSelect_Max 函数用于找到数组中最大的前 N 个元素 void TopKSelect_Max(int N, int K) { 
    // 创建一个大小为 N 的最大堆 Heap<T> vt(N); // 将前 N 个元素插入堆中 for(int i = 0; i < N; i++) { 
    vt.insert(_data[i]); } // 调整堆结构，使其满足最大堆的性质 for(int i = (N - 1 - 1)/2; i >= 0; i--) { 
    vt.AdjustDown_to_Min(i,N); } // 遍历剩余的 K-N 个元素 for (int i = N; i < K; i++) { 
    // 如果当前元素大于堆顶元素，则替换堆顶元素 if (vt._data[0] < _data[i]) { 
    vt._data[0] = _data[i]; } // 调整堆结构，使其满足最大堆的性质 vt.AdjustDown_to_Min(0,N); } // 打印最大堆 vt.printHeap(); } // TopKSelect 函数用于根据 flag 参数选择找到数组中最大的前 N 个元素或最小的前 N 个元素 void TopKSelect(int N, int K, bool flag) { 
    if(flag == true) // 选前 N 个最小的数 { 
    TopKSelect_Min(N, K); } else if(flag == false) // 选前 N 个最大的数 { 
    TopKSelect_Max(N, K); } } 

int main() { 
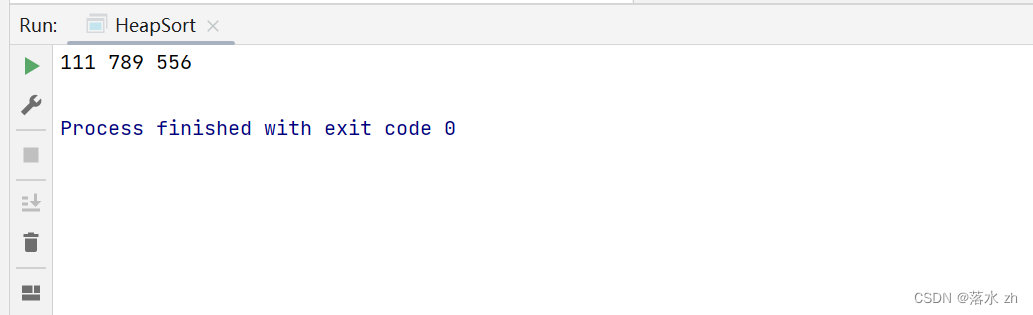
    std::vector<int> vt ={ 
   1,34,6,111,789,0,23,556,11,4,74}; Heap<int> newheap(vt); newheap.TopKSelect(3,vt.size(),false); return 0; } 

 std::vector<int> vt ={ 
   1,34,6,111,789,0,23,556,11,4,74}; Heap<int> newheap(vt); newheap.TopKSelect(3,vt.size(),true); 

如果大家还有不了解的地方，可以点击这里，这里是我以前写的关于堆的博客：

十大排序——堆排序

递归版本

这里的递归版本也是锻炼思维，实际中不会这样用：

// 该函数用于调整从指定索引开始的小顶堆，使其满足堆性质 void Adjust_Up(int *array, int size, int index) { 
    // 如果索引超出了堆的有效范围（即超过了最后一个非叶子节点），则停止调整 if(index > size - 1) return; // 递归调整左子节点 Adjust_Up(array, size, 2*index + 1); // 递归调整右子节点 Adjust_Up(array, size, 2*index + 2); // 计算当前节点的父节点索引 int parent = (index - 1) / 2; // 如果父节点索引小于0，意味着当前节点已经是根节点，无需继续调整 if(parent < 0) return; // 如果父节点的值大于当前节点的值，交换它们以满足小顶堆性质 if (array[parent] > array[index]) std::swap(array[parent],array[index]); } // 向下调整算法，用于维护从指定索引开始的小顶堆性质 void Adjust_Down(int* array, int size, int index) { 
    // 如果当前索引超出了数组的有效范围（即它是叶子节点或不存在的索引），则不需要调整 if (index > size - 1) return; // 递归地对左子节点进行向下调整 Adjust_Down(array, size, 2 * index + 1); // 递归地对右子节点进行向下调整 Adjust_Down(array, size, 2 * index + 2); // 初始化子节点的索引为当前节点的左子节点 int child = 2 * index + 1; // 如果子节点索引超出了数组的有效范围，说明当前节点是叶子节点，无需调整 if (child > size - 1) return; // 找出左右子节点中较小的那个（小顶堆中需要父节点小于或等于子节点） // 如果右子节点存在且其值小于左子节点，则选择右子节点 if (child + 1 < size && array[child] > array[child + 1]) child++; // 如果当前节点的值大于其较小子节点的值，则交换它们以维护小顶堆性质 if (array[index] > array[child]) { 
    std::swap(array[index], array[child]); // 交换后可能破坏了子树的堆性质，需要对交换后的子节点继续进行向下调整 // 注意：这里的递归调用在C++标准库的实现中常见，但在某些场景下可能不是最优解，实际应用中可能需要考虑迭代法替代 Adjust_Down(array, size, child); } else { 
    // 如果当前节点不大于子节点，则堆性质已经满足，直接结束 return; } } void Heap_sort(int *array,int size) { 
    if(size == 0) return; Adjust_Down(array,size,0); int end = size - 1; std::swap(array[0],array[end]); Heap_sort(array,end); } int main() { 
    int a[] = { 
    1,34,2,77,8,100,-1,23,999,1234,99,1,-99,0,8,1,33,71 }; int size = sizeof(a) / sizeof(a[0]); for(int i = 0; i < size; i++) { 
    std::cout << a[i] << " "; } std::cout << std::endl; //Adjust_Down(a,size,0); Adjust_Up(a,size,0); for(int i = 0; i < size; i++) { 
    std::cout << a[i] << " "; } std::cout << std::endl; Heap_sort(a,size); for(int i = 0; i < size; i++) { 
    std::cout << a[i] << " "; } std::cout << std::endl; }