4.2、矩阵转置

大家好，欢迎来到IT知识分享网。

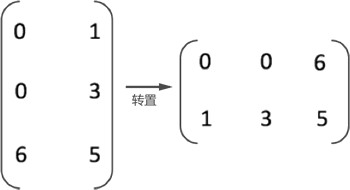
• 矩阵转置：互换矩阵中所有元素的行标和列标

  

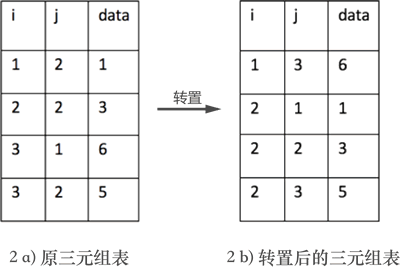
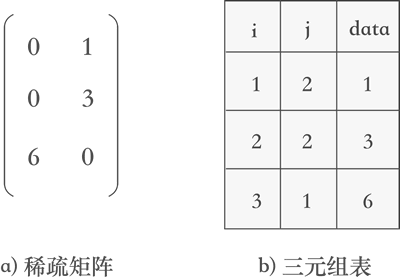
• 如果想通过程序实现矩阵的转置，互换行标和列标只是第一步。因为实现矩阵转置的前提是将矩阵存储起来，数据结构中提供了 3 种存储矩阵的结构：三元组顺序表、行逻辑链接的顺序表和十字链表。如果采用前两种结构，矩阵的转置过程会涉及三元组表也跟着改变的问题，如下图所示：

  

• 不仅如此，如果矩阵的行数和列数不等，也需要将它们互换。
• 因此，矩阵转置需完成以下 3 步：

• • 将矩阵的行数和列数互换
  • 将三元组表（存储矩阵）中的 i 列和 j 列互换，实现矩阵的转置
  • 以 j 列为序，重新排列三元组表中存储各三元组的先后顺序

• 前两步比较简单，关键在于最后一步的实现。

1、矩阵转置的普通算法

• 矩阵转置的实现思路：不断遍历存储矩阵的三元组表，每次都取出表中 j 列最小的那一个三元组，互换行标和列标的值，并按次序存储到一个新三元组表中。
• 例如，将图 2a) 三元组表存储的矩阵进行转置的过程：

1. 1. 新建一个三元组表（用于存储转置矩阵），并将原矩阵的行数和列数互换赋值给新三元组
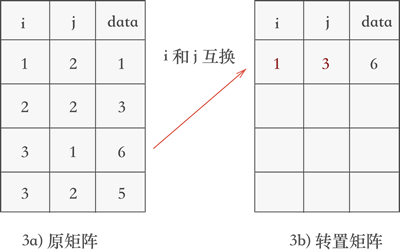
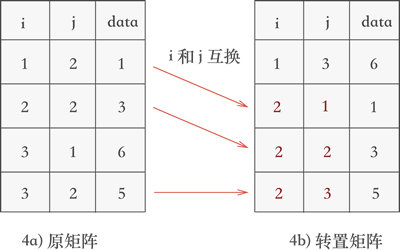
   2. 遍历三元组表，找到表中 j 列最小值 1 所在的三元组(3,1,6)，然后将其行标和列标互换后添加到一个新的三元组表中：

      

   3. 继续遍历三元组表，找到表中 j 列次小值为 2 的三元组，分别为(1,2,1)、(2,2,3)和 (3,2,5)，根据找到它们的先后次序将各自的行标和列标互换后添加到新三元组表中：

      

• • 矩阵被成功地转置。

• 矩阵转置（C 语言）：

#include<stdio.h> #define number 10 typedef struct { int i, j; int data; }triple; typedef struct { triple data[10]; int n, m, num; }TSMatrix; TSMatrix transposeMatrix(TSMatrix M, TSMatrix T) { T.m = M.n; T.n = M.m; T.num = M.num; if (T.num) { int q = 0; for (int col = 1; col <= M.m; col++) { for (int p = 0; p < M.num; p++) { if (M.data[p].j == col) { T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].data = M.data[p].data; q++; } } } } return T; } int main() { TSMatrix M; M.m = 2; M.n = 3; M.num = 4; M.data[0].i = 1; M.data[0].j = 2; M.data[0].data = 1; M.data[1].i = 2; M.data[1].j = 2; M.data[1].data = 3; M.data[2].i = 3; M.data[2].j = 1; M.data[2].data = 6; M.data[3].i = 3; M.data[3].j = 2; M.data[3].data = 5; TSMatrix T; for (int k = 0; k < number; k++) { T.data[k].i = 0; T.data[k].j = 0; T.data[k].data = 0; } T = transposeMatrix(M, T); for (int i = 0; i < T.num; i++) { printf("(%d,%d,%d)\n", T.data[i].i, T.data[i].j, T.data[i].data); } return 0; } /* (1,3,6) (2,1,1) (2,2,3) (2,3,5) */

2、稀疏矩阵的快速转置算法

• 稀疏矩阵快速转置算法和普通算法的区别仅在于第 3 步：快速转置做到遍历一次三元组表即可完成第 3 步的工作。
• 稀疏矩阵和对应的三元组表：

  

• 稀疏矩阵的快速转置：在普通算法的基础上增设两个数组 array 和 copt：

• • array 数组记录原矩阵每一列非 0 元素的个数。上图对应的 array 数组如下（原稀疏矩阵中第一列有 1 个非 0 元素，第二列有 2 个非 0 元素）：

    

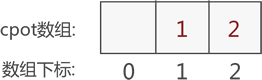
  • copt 数组用于计算稀疏矩阵中每列第一个非 0 元素在新三元组表中存放的位置（通常默认第一列首个非 0 元素存放到新三元组表中的位置为 1），然后通过cpot[col] = cpot[col-1] + array[col-1]公式计算出后续各列首个非 0 元素存放到新三元组表的位置。上图稀疏矩阵对应的 copt 数组如下（原稀疏矩阵中第 2 列首个非 0 元素存放到新三元组表的位置为 2）：

    

• cpot[col] = cpot[col-1] + array[col-1]表示后一列首个非 0 元素存放的位置等于前一列首个非 0 元素的存放位置加上该列非 0 元素的个数。由此可看出，copt 数组才是最终想要的，而 array 数组的设立只是为了帮助我们得到 copt 数组。
• 在实现第 3 步时，根据每个三元组中 j 的数值，可以借助 cpot 数组直接得到此三元组新的存放位置，C 语言实现代码：

// 实现快速转置算法的函数 TSMatrix fastTransposeMatrix(TSMatrix M,TSMatrix T){ // 第 1 步：行和列置换 T.m=M.n; T.n=M.m; T.num=M.num; if (T.num) { // 计算 array 数组 int array[number]; for (int col=1; col<=M.m; col++) { array[col]=0; } for (int t=0; t<M.num; t++) { int j=M.data[t].j; array[j]++; } // 创建并初始化 cpot 数组 int cpot[T.m+1]; // 第一列中第一个非 0 元素的位置默认为 1 cpot[1]=1; for (int col=2; col<=M.m; col++) { cpot[col]=cpot[col-1]+array[col-1]; } // 遍历一次即可实现三元组表的转置 for (int p=0; p<M.num; p++) { // 提取当前三元组的列数 int col=M.data[p].j; // 根据列数和 cpot 数组, 找到当前元素需要存放的位置 int q=cpot[col]; // 转置矩阵的三元组默认从数组下标 0 开始, 而得到的 q 值是单纯的位置, 所 // 以要减 1 T.data[q-1].i=M.data[p].j; T.data[q-1].j=M.data[p].i; T.data[q-1].data=M.data[p].data; // 存放完成后, cpot 数组对应的位置要 +1, 以便下次该列存储下一个三元组 cpot[col]++; } } return T; }

• 使用 fastTransposeMatrix 函数实现稀疏矩阵转置（C 语言）【undo】：

#include<stdio.h> #define number 10 typedef struct { int i,j; int data; }triple; typedef struct { triple data[number]; int rpos[number]; int n,m,num; }TSMatrix; // fastTransposeMatrix 放置位置 int main() { TSMatrix M; M.m=2; M.n=3; M.num=3; M.data[0].i=1; M.data[0].j=2; M.data[0].data=1; M.data[1].i=2; M.data[1].j=2; M.data[1].data=3; M.data[2].i=3; M.data[2].j=1; M.data[2].data=6; TSMatrix T; T=fastTransposeMatrix(M, T); printf("转置矩阵三元组表为：\n"); for (int i=0; i<T.num; i++) { printf("(%d,%d,%d)\n",T.data[i].i,T.data[i].j,T.data[i].data); } return 0; } /* 转置矩阵三元组表为： (1,3,6) (2,1,1) (2,2,3) */