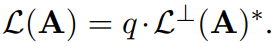格密码基础：详解LWE问题

大家好，欢迎来到IT知识分享网。

一. 介绍

Learning With Errors 简称 LWE，通常翻译为容错学习问题。

在2005年，Regev首次提出了平均情况下的LWE问题。类似SIS问题，LWE也可以用来实现加密。这两类问题实际上互为对偶（dual）关系。接下来我们将介绍LWE的困难性以及基于LWE的密码系统。进阶的内容则包含LWE最坏情况的困难性，以及search和decision版本之间的归约。

SIS问题可参看：

格密码基础：SIS问题的定义与理解-CSDN博客

二. LWE分布

LWE问题有三个重要的参数：整数n，模q和整数上的误差分布X。此处的n和q的理解与SIS类似，分布X可以看成离散高斯分布，其宽度（width）为：

$\alpha q\quad \alpha<1$

此处的宽度类似高斯分布的标准差，可以被称之为相对误差率（relative error rate）。

备注：对于连续的高斯分布（continuous Gaussian distribution），借鉴随机离散化算法便可以形成离散的高斯分布（直观上，我们可以看成对连续高斯分布进行就近取整）。

有一个n维的秘密列向量s，如下：

$s\in Z_q^n$

均匀且随机的选择一个公开的n维列向量a：

$a\in Z_q^n$

接着从分布X中随机选择e：

$e\leftarrow X$

接着计算如下：

$(a,b=\langle s,a\rangle+e\quad mod\ q)$

随着a在不断变化，该形式可形成一个分布，我们称之为LWE分布。再根据a和b的形式，可得该分布的维度如下：

$Z_q^n\times Z_q$

三. LWE问题的两个版本

LWE问题最常用两个版本。给出LWE的样本，让你去求秘密向量s，则称之为search问题。

抽取LWE样本，从均匀且随机的分布中抽取样本，让你进行区分这两种情况，称之为decision问题。

细心的小伙伴会发现，以上抽取样本，通常有多少个呢？

可设定为样本个数有m个，当然为了保证秘密s唯一可解，通常需要要求m>n。这也是LWE问题与SIS问题的区别之一。

3.1 search LWE问题

我们通常将LWE分布记作：

$A_{s,X}$

对于固定的秘密向量s：

$s\in Z_q^n$

从LWE分布中随机抽取m个独立的样本，如下：

$(a_i,b_i)\in Z_q^n\times Z_q$

根据这些样本，求取s的过程，则称之为LWE-search问题，完整表达如下：

$Search-LWE_{n,q,X,m}$

完整的英文形式化表达如下：

3.2 decision LWE问题

给定m个独立的样本，如下：

$(a_i,b_i)\in Z_q^n\times Z_q$

这些样本来源的分布有两种情况：

（1）均匀随机的 $s\in Z_q^n$ ，接着固定s，形成分布 $A_{s,X}$

（2）真均匀且随机的分布

如果能以不可忽略的优势区分这两种情况，才可以称之为解决了decision LWE问题。

四. LWE的性质

4.1 误差e的重要性

如果没有来源于分布X的误差项，那么以上LWE问题就都可以被解决。比如借助高斯消元法（Gaussian elimination）可以从LWE样本中恢复出s。

在decision-LWE问题中，对于真均匀分布的情况，可以大概率确定s不存在，也就可以区分开来了。

4.2 矩阵形式

在网络安全等领域，通常会把以上样本结合成矩阵A:

$A\in Z_q^{n\times m}$

矩阵A的每一列都代表一个向量 $a_i\in Z_q^n$

同理，b也可以形成向量：

$b\in Z_q^n\quad b_i\in Z_q$

结合以上形式，我们可以将LWE样本写成：

其中误差e：

$e\leftarrow X^m$

如果是真的成均匀分布中选取，也就是在decision LWE问题中,b就是真随机的，且与矩阵A无关。

4.3 LWE与BDD问题

bounded-distance decoding 简称 BDD，中文通常翻译为：有限距离解码问题

我们知道，对于任意LWE样本，向量b与LWE格是很接近的，中间差一个误差e。LWE就是我们通常所说的m维q-ary格，如下：

所以可以把LWE问题看成寻找格点的过程，也就可以把search-LWE问题看成平均情况的BDD问题。

如果向量b来源于均匀分布，那么其大概率跟格L(A)中的所有格点都很远。

根据LWE与SIS之间的关系，其实我们可以得到两者之间互为q倍对偶关系：

4.4 LWE与隐藏超平面问题

观察LWE的样本：

$(a_i,b_i)\in Z_q^{n+1}$

可对样本的横坐标与纵坐标做如下运算：

那么我们可以发现LWE跟垂直于（-s,1）的子空间很接近，当然所有的运算都在模q下，所以我们发现这个跟Ajtai-Dwork发现的隐藏超平面问题非常类似。

五. 推荐文献

（1）解释LWE与隐藏超平面之间的关系

O. Regev. The learning with errors problem (invited survey). In IEEE Conference on Computational Complexity, pages 191–204. 2010.

（2）完整介绍LWE问题

（3）Regev对格密码介绍的课件

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/124447.html

格密码基础：详解LWE问题

一. 介绍

二. LWE分布

三. LWE问题的两个版本

3.1 search LWE问题

3.2 decision LWE问题

四. LWE的性质

4.1 误差e的重要性

4.2 矩阵形式

4.3 LWE与BDD问题

4.4 LWE与隐藏超平面问题

五. 推荐文献

相关推荐

发表回复