查找（二）—— 折半查找

大家好，欢迎来到IT知识分享网。

折半查找——只能用于有序顺序表的查找

1.什么是折半查找

        折半查找（又称二分查找）是一种用于在有序数组中查找特定元素的算法。它的基本思想是将有序数组分成两个部分，找到中间元素，与要查找的关键字进行比较，如果相等，则查找成功；如果要查找的关键字比中间元素小，则在左半部分继续查找；如果要查找的关键字比中间元素大，则在右半部分继续查找。通过不断的缩小查找范围，最终可以找到要查找的元素。

        折半查找的时间复杂度为 O(log n)，比顺序查找的时间复杂度 O(n) 要更快。因此，折半查找是一种非常高效的查找算法。

2.折半查找实现过程 

        上述顺序表折半查找31过程如下：

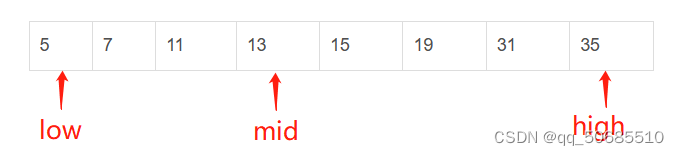
                第一步：设定头指针，尾指针，。

                 第二步：mid元素与31比较。因为13<31，则，不变，。

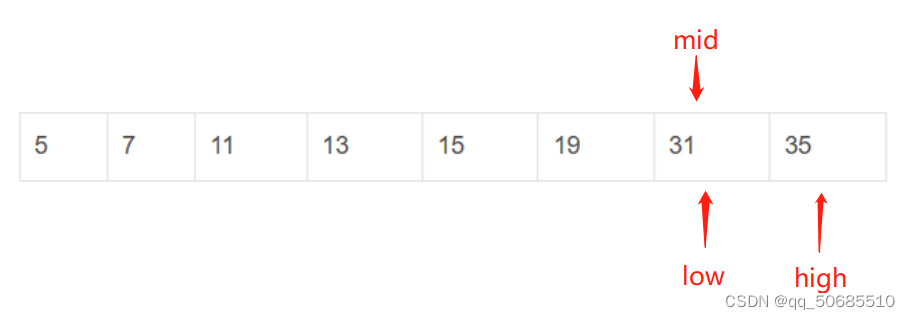
                 第三步：mid元素与31比较。因为19<31，则，不变，。

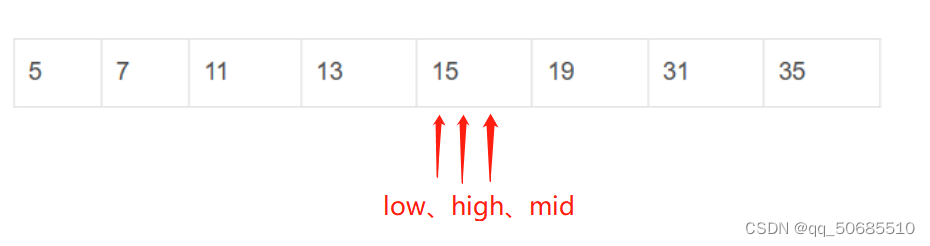
                 第四步：mid元素与31比较。因为31=31，则已经找到，退出循环。

        上述顺序表折半查找14过程如下：

                第一步：设定头指针，尾指针，。

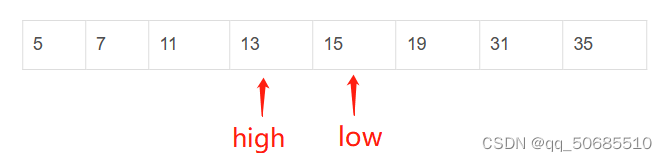
                 第二步：mid元素与14比较。因为13<14，则，不变，。

                第三步：mid元素与14比较。因为19>14，则，不变，。 

                 第四步：mid元素与14比较。因为15>14，则，不变为4,此时high”>，跳出循环，即14不在该数组中。

                 c语言代码如下：

int Binary_search(int *array,int length,int key){ int low = 0,high = length-1,mid; while(low <= high){ //退出循环条件为low>high mid = (low+high)/2; if(array[mid] == key) return mid; //找到 else if(array[mid] > key) high = mid-1; //key在mid左边 else low = mid+1; //key在mid右边 } return -1; //未找到 } 

3.折半查找的描述——判定树

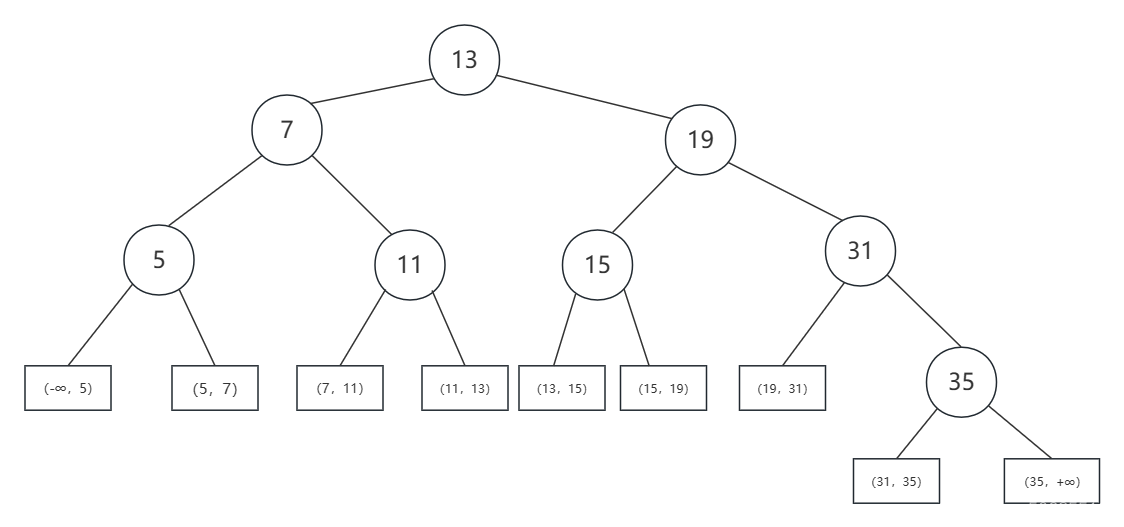
        以上述有序数组为例子构建判定树，如下图所示：

         每个圆形结点就是一个记录，结点中的值为该记录的关键数值；树下面的叶结点是方形的，表示查找不成功的情况。从判定树可以看出，查找成功的查找长度为从根节点到目的结点路径上的结点数，而查找不成功的查找长度为从根节点到对应失败结点的父结点的路径上的结点数；每个结点都大于左边子结点的值，小于右边子结点的值。若有序序列有n个元素，则对应的判定数有n个圆形结点和n+1个方形叶结点，判定树是一颗平衡树。折半查找时间复杂度为。

4.折半查找的递归实现

         折半查找该算法具有明显的规律性，可以用递归算法加以实现，实现逻辑与普通循环逻辑一致，C程序代码如下：

int dgBinary_search(int low,int high,int *array,int key){ if(low > high) return -1; if(array[(low+high)/2] == key) return (low+high)/2; else if(array[(low+high)/2] > key) return dgBinary_search(low,(low+high)/2-1,array,key); else if(array[(low+high)/2] < key) return dgBinary_search((low+high)/2+1,high,array,key); }

        跳出递归的两种情况：Ⅰ找到key，return数组下标 Ⅱ没有找到key，return -1表示没找到。

        其余如果key在mid左边，则函数调用自己将high参数变为mid-1，如果key在mid右边，则函数调用自己将low参数变为mid+1。

5.折半查找的经典例题

     leetcode35题：搜索插入位置      

       给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

        示例 :

        输入: nums = [1,3,5,6], target = 5         输出: 2 

        该题直接套用折半查找算法即可，只需在没找到的情况下判断mid在插入位置左侧还是右侧即可。代码如下：

int searchInsert(int* nums, int numsSize, int target){ int low = 0,mid,high = numsSize - 1; while(low <= high){ mid = (high + low)/2; if(nums[mid] == target) return mid; else if(nums[mid] > target) high = mid-1; else if(nums[mid] < target) low = mid+1; } if(target > nums[mid]) //表明插入位置在mid后 return mid + 1; else return mid; }