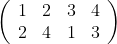大家好,欢迎来到IT知识分享网。
目录
一,映射、变换、置换
1,映射
集合A到集合B可以定义一个映射。
映射根据是否是单射,是否是满射,可以分为非单非满映射、单射非满射、满射非单射、一一映射四种。
2,变换
集合A到自身的映射,叫做变换。
很自然的就有集合A上的单射变换、满射变换和一一变换。
一一映射、一一变换、恒等映射、恒等变换都是一个意思。
3,置换
如果A是有限集合,那么A上的变换叫做置换。
标准记法:
简化记法:
(2 4 1 3)
二,变换群、置换群、对称群(全置换群)
1,变换群
由若干变换为元素,复合作为运算的群,叫做变换群。
2,置换群
由若干置换为元素,复合作为运算的群,叫做置换群。
3,对称群(全置换群)
由n个元素的全部置换所构成的群,称为对称群Sn,也叫全置换群。
根据定义,对称群具备下列属性:
二元运算:复合(composition,该运算具备结合性)
取逆运算:逆置换(inverse permutation)
单位元素:恒等置换(identity permutation)
三,凯莱定理
凯莱定理:凡是元素个数为n的群,都与对称群Sn的某子群同构。
PS:这个定理的证明没怎么研究。
四,换位
换位,是交换第i与第j个元素(i≠j),并保持其余元素不动的置换。
C++中的交换swap和换位意思差不多。
swap操作只要求其参数满足Semiregular这一concept即可,不一定非得是Regular才行。
换位引理:任何一种置换方式,都是若干换位的乘积。
五,置换分解成循环
置换可以分解成若干个循环。
这种分解可以记为()=(1235)(46)
包含一个元素的循环,称为平凡循环。
每个长度为k的非平凡循环,都需要用k+1次赋值操作才能完成。
原地执行任意一种置换方式,需要使用n-u+v次赋值操作,其中n是元素个数,u与v分别是该置换方式中的平凡与非平凡循环个数。
六,交换两个区间
可以用first0与last0来表示第一个区间的左界和右界,并且用first1来表示第二个区间的左界:
我们为了能在数据上面调用swap操作,必须保证I0的值类型与I1的值类型相同。由于concept还未正式融入C++语言,因此我们在代码中,暂时以注释来表达这一要求。
这里演示了一条重要的编程原则:类型分离原则。
如果两份数据有可能是不同的类型,那么就不要假设它们必然是同一个类型。
上面的2个迭代器类型可以不同,所以我们可以用来交换链表的一段和数组的一段。
七,旋转(rotation)
将n个元素根据k值(k≥0)做如下形式的转置:(k mod n,k+1 mod n,…,k+n-2 mod n,k+n-1 mod n)称为n个元素的k次旋转。
旋转的Gries-Mills算法:
如果rotate算法,能够返回参数m在算法执行完毕时所具备的新值,那么会对很多计算场景都有所帮助,因为该值反映了旋转前的首个元素,在旋转后所处的位置。有了这个值,就可以通过rotate(f,rotate(f,m,l),l)来实现恒等置换。
算法的赋值次数是 3(n-gcd(n,k))
Gries-Mills算法每次移动时,都只需前进一个位置,也就是说,该算法可以用于单链表这样的数据结构。
八,利用循环来执行旋转
n个元素的k次旋转,含有gcd(k,n)个循环,因此,只需做n+gcd(k,n)次赋值即可。
借助循环来实现的旋转算法,需执行跨度大于1的跳跃,这意味着它对迭代器的要求比前者高,换句话说,它要求迭代器必须支持随机访问。
首先我们实现单个循环:
template <ForwardIterator I, Transformation F> void rotate_cycle_from(I i, F from) { ValueType<I> tmp = *i; I start = i; for (I j = from(i); j = start; j = from(j)) { *i = *j, i = j; } *i = tmp; }这个rotate_cycle_from函数可以完成迭代器i所在的循环,from是跳跃访问的迭代器,可以把from(i)理解成:计算i位置上的元素来自何处。
利用循环来执行旋转:
九,倒置
倒置(reverse)就是对含有k个元素的列表进行置换,使得第0个与第k-1个元素互换、第1个与第k-2个元素互换,依此类推。
用倒置实现旋转:
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/124958.html