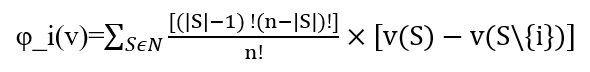Shapley值法介绍及实例计算

大家好，欢迎来到IT知识分享网。

前言

一、 Shapley值法解析

（一）符号定义

（二）Shapley值法的公理

（3）冗员性
      若对于包含成员i的所有子集S都有v(S{i})=v(S)，则φ_i(v)=0。其中S{i}为集合S去掉元素 i 后的集合。
      这说明如果一个成员对于任何他参与的合作联盟都没有贡献，则他不应当从全体合作中获利。
（4）加法性
      若在N上有两个特征函数v, w，则有

（三）Shapley值法

      成员i在参与S联盟时有(|S|-1)!种排序，|S|表示联盟S所包含的成员数，而剩余(n-|S|)个成员的排序有(n-|S|)!种，所有成员i参与的不同的排序组合除以n个成员的随机排序组合就是成员i对于联盟整体所应分得利益得权重，记为 [(|S|-1) !(n-|S|)!]/(n!) 。成员i参与不同联盟S为自身参与联盟创造得 边际贡献 记为 [v(S)-v(S\ {i})] ，那么成员i从总体利益v(N)所分得的利益为：

注：S\ {i}表示从集合S中删除元素 i 后的集合。

二、 实例

      题目：共有三家公司，公司1，2，3单独投资可盈利v(1)=100，v(2)=200，v(3)=300，如果公司1和公司2联合，可获利v(1&2)=500；公司2和公司3联合，可获利v(2&3)=600；公司1和公司3联合，可获利v(1&3)=700；公司1、公司2和公司3联合，可获利v(1&2&3)=1000；那么三个公司一起合作，每个公司应各获利多少？

解析一

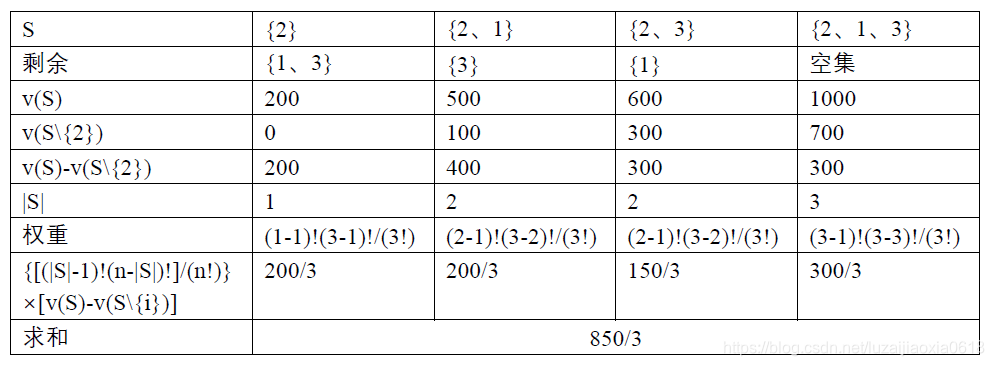
（2）成员2 获利：

      成员2（公司2）的获利为850/3。

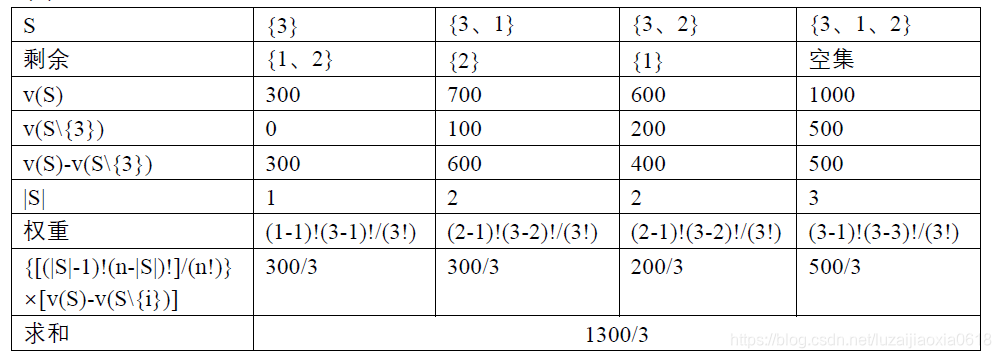
（3）成员3 获利：

      因此成员3（公司3）的获利为1300/3。

（4）三者获利和总为（850/3+850/3+1300/3）=1000，符合题目。

解析二

参考文献

注：这是笔者学习Shapley值法的总结，如有错误敬请包涵，欢迎评论交流~