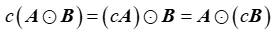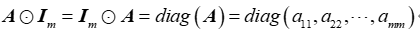哈达玛积（Hadamard）和克罗内克积（Kronecker积）

大家好，欢迎来到IT知识分享网。

1、Hadamard积

考虑两个矩阵之间的直接乘积。

定义： $m\times n$ 矩阵 $\mathbf{A}=\left [ a_{ij} \right ]$ 与 $m\times n$ 矩阵 $\mathbf{B}=\left [ b_{ij} \right ]$ 的Hadamard积记作 $\mathbf{A}\odot \mathbf{B}$ ，它仍然是一个 $m\times n$ 矩阵，定义为

$\mathbf{A}\odot \mathbf{B}=\left [ a_{ij} b_{ij}\right ]$

Hadamard积也称为Schur积或者对应元素乘积。矩阵Hadamard积的一个重要结果是下面的Hadamard积定理。

定理：若 $m\times m$ 矩阵是正定（或半正定）的，则它们的Hadamard积 $\mathbf{A}\odot \mathbf{B}$ 也是正定（或半正定）的。

推论(Fejer定理)：令A是一个 $m\times m$ 矩阵，则A是半正定当且仅当 $\sum_{i=q}^{m}\sum_{j=1}^{m}a_{ij}b_{ij}\geq 0$ 对所有 $m\times m$ 半正定矩阵B成立。

下面两个定理描述了矩阵的Hadamard积与迹之间的关系：

定理：令A,B,C为 $m\times n$ 矩阵，并且 $\mathbf{1}=\left [1,1,\cdots ,1 \right ]^{T}$ 为 $n\times 1$ 求和向量， $\mathbf{D}=diag\left ( d_{1},d_{2},\cdots ,d_{m} \right )$ ，其中， $d_{i}=\sum_{j=1}^{n}a_{ij}$ ，则

定理：令A,B为正方矩阵，并且 $\mathbf{1}=\left [1,1,\cdots ,1 \right ]^{T}$ 为 $n\times 1$ 求和向量，假设M是一个 $n\times n$ 对角矩阵 $\mathbf{M}=diag\left ( \mu _{1},\mu_{2},\cdots ,\mu _{n} \right )$ ，而 $\mathbf{m}=\mathbf{M}\mathbf{1}$ 为 $n\times 1$ 向量，则有

Hadamard积具有以下性质：

(1) 若A,B均为 $m\times n$ 矩阵，则

(2) 任何一个 $m\times n$ 矩阵A与 $m\times n$ 零矩阵 $\mathbf{O}_{m\times n}$ 的Hadamard积等于 $m\times n$ 零矩阵，即 $\mathbf{A}\bigodot\mathbf{O}_{m\times n}=\mathbf{O}_{m\times n}\bigodot \mathbf{A}=\mathbf{O}_{m\times n}$ 。

(3) 若c为常数，则

(4) 矩阵 $\mathbf{A}_{m\times m}=\left [ a_{ij} \right ]$ 与单位矩阵 $\mathbf{I}_{m}$ 的Hadamard积为 $m\times m$ 对角矩阵，即

(5) 若A,B,C,D均为 $m\times n$ 矩阵，则

(6) 若A,C为 $m\times m$ 矩阵，并且B,D为 $n\times n$ 矩阵，则

(7) 若A,B,C为 $m\times n$ 矩阵，则

(8) 若A,B,D为 $m\times m$ 矩阵，则

(9) 若 $m\times m$ 矩阵A,B是正定的(或半正定)的，则它们的Hadamard积 $\mathbf{A}\bigodot \boldsymbol{B}$ 也是正定(或半正定)的。

tip：关于Hadamard积的具体证明可自行查阅张贤达的《矩阵分析与应用》。

2、Kronecker积

Kronecker积是表示矩阵特殊乘积的一种简洁数字符号。一个 $m\times n$ 矩阵A和一个 $p\times q$ 矩阵B的Kronecker积记作 $\mathbf{A}\otimes \mathbf{B}$ ，它是一个 $mp\times nq$ 矩阵。

Kronecker积也称直积（direct product）或者张量积（tensor product）。

定义（右Kronecker积）： $m\times n$ 矩阵A和 $p\times q$ 矩阵B的右Kronecker积 $\mathbf{A}\otimes \mathbf{B}$ 定义为

更具体可以表示为

定义（左Kronecker积）： $m\times n$ 矩阵A和 $p\times q$ 矩阵B的左Kronecker积 $\mathbf{A}\otimes \mathbf{B}$ 定义为

若矩阵 $\mathbf{A}_{m\times n}=\mathbf{a}\mathbf{b}^{T}$ ，则

如下面定理所述，向量化算子这一性质公式可以推广为矩阵乘积的向量化公式。

定理：令 $\mathbf{A}_{m\times p},\mathbf{B}_{p\times q},\mathbf{C}_{q\times n}$ ，则

Kronecker积具有以下性质：

(1) 对于矩阵 $\mathbf{A}_{m\times n}$ 和 $\mathbf{B}_{p\times q}$ ，一般有 $\mathbf{A}\bigotimes \mathbf{B}\neq \mathbf{B}\bigotimes \mathbf{A}$ 。

(2) 任意矩阵与零矩阵的Kronecker积等于零矩阵，即 $\mathbf{A}\bigotimes \mathbf{O}\neq \mathbf{O}\bigotimes \mathbf{A}=\mathbf{O}$

(3) 若 $\alpha$ 和 $\beta$ 为常数，则

(4) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{n\times k},\mathbf{C}_{l\times p},\mathbf{D}_{p\times q}$ ，有

(5) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q},\mathbf{C}_{p\times q}$ ，有

(6) 若矩阵A和B分别有广义逆矩阵 $\mathbf{A}^{\dagger }$ 和 $\mathbf{B}^{\dagger }$ ，则

特别地，若A和B是可逆的正方矩阵，则

(7) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q}$ ，有

(8) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q}$ ，有

(9) 若A是 $m\times m$ 矩阵，B是 $n\times n$ 矩阵，则

(10) 若A是 $m\times m$ 矩阵，B是 $n\times n$ 矩阵，则

$tr\left ( \mathbf{A}\bigotimes \mathbf{B} \right )=tr\left ( \mathbf{A} \right )tr\left ( \mathbf{B} \right )$

(11) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{m\times n},\mathbf{C}_{p\times q},\mathbf{D}_{p\times q}$ ，有

更一般地，有

(12) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{k\times l},\mathbf{C}_{p\times q},\mathbf{D}_{r\times s}$ ，有

(13) 若 $\alpha _{i}$ 是矩阵A与特征值 $\lambda _{i}$ 对应的特征向量， $\beta _{i}$ 是矩阵B与特征值 $\mu _{i}$ 对应的特征向量，则 $\alpha _{i}\bigotimes \beta _{i}$ 是矩阵 $\mathbf{ A}\bigotimes \mathbf{B}$ 与特征值 $\lambda _{i}\mu _{i}$ 对应的特征向量，也是与特征值 $\lambda _{i}+\mu _{i}$ 对应的特征向量。

(14) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q},\mathbf{C}_{k\times l}$ ，有

(15) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q},\mathbf{C}_{n\times r},\mathbf{D}_{q\times s}$ ，有

更一般地，有

和

(16) 对于矩阵 $\mathbf{A}_{m\times n},\mathbf{B}_{p\times q}$ ，有

$exp\left (\mathbf{ A}\bigotimes \mathbf{B} \right )=exp\left ( \mathbf{A }\right )\bigotimes exp\left ( \mathbf{B} \right )$

(17) 作为性质(15)的特例，若 $\mathbf{B}=\mathbf{I}_{p}$ 和 $\mathbf{C}=\mathbf{I}_{q}$ ，则

式中， $\mathbf{I}_{p}\bigotimes \mathbf{D}$ 为块对角矩阵（对右Kronecker积）或稀疏矩阵（对左Kronecker积），而 $\mathbf{A}\bigotimes \mathbf{I}_{q}$ 为稀疏矩阵（对右Kronecker积）或块对角矩阵（对左Kronecker积）。

tip：关于Kronecker积的具体证明可自行查阅张贤达的《矩阵分析与应用》。

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/127567.html

哈达玛积（Hadamard）和克罗内克积（Kronecker积）

1、Hadamard积

2、Kronecker积

相关推荐

发表回复