FSK调制解调

大家好，欢迎来到IT知识分享网。

1.FSK调制解调原理

1.1FSK时域信号

数字频率调制（FM）是利用载波的频率传输信息的一种调制方式，其中最简单的是二进制频移键控（2FSK）。FM分为非连续相位FSK和连续相位FSK（CPFSK），两者的区别在于码元转换时刻的载波相位是否连续。

1.2相关系数与频谱特性

CPFSK信号的功率谱形状直接由调制指数h确定。当h=0.5时，功率谱曲线为单峰；当h=0.715时，功率谱曲线呈现双峰；当h=1时，功率谱曲线的双峰变成了两条线状谱，且每条线状谱所占的功率都是信号功率的1/4，与离散相位2FSK信号的功率谱曲线相同；当h>1时，双峰的距离逐渐增加。

1.3非相干解调

1.3.1相乘微分型AFC环解调法

1.3.2包络检波解调法

1.4相干解调原理

1.4.1最佳FSK相干解调器

1.4.2易于实现的FSK相干解调器

2.FSK的MATLAB仿真

2.1FSK信号产生

ps=1*10^6; %码速率为1MHz N=1000; %数据码元个数 Fs=32*10^6; %采样速率为32MHz fc=6*10^6; %载波频率为6MHz Len=N*Fs/ps; %仿真调制指数为0.5时的FSK信号 m=0.5; %调制指数 freqsep=m*ps; %FSK信号中，两个频率之间的间隔 nsamp=Fs/ps; %每个码元的采样点数 x = randint(N,1,2); % 产生随机数据做为数据码元 ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont'); % 产生连续相位FSK调制信号的正交基带数据 DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据 %将基带FSK信号正交上变频至6MHz中频 t=0:1/Fs:(Len-1)/Fs; f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1); Contfsk=real(ContData.*f0'); DisContfsk=real(DisContData.*f0'); %计算FSK信号的幅频特性 m_ContFsk=20*log10(abs(fft(Contfsk,2048))); m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));; m05_ContFsk=m_ContFsk-max(m_ContFsk); m05_DisFsk=m_DisFsk-max(m_DisFsk); %仿真调制指数为0.715时的FSK信号 m=0.715; %调制指数 freqsep=m*ps; %FSK信号中，两个频率之间的间隔 nsamp=Fs/ps; %每个码元的采样点数 x = randint(N,1,2); % 产生随机数据做为数据码元 ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont'); % 产生连续相位FSK调制信号的正交基带数据 DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据 %将基带FSK信号正交上变频至6MHz中频 t=0:1/Fs:(Len-1)/Fs; f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1); Contfsk=real(ContData.*f0'); DisContfsk=real(DisContData.*f0'); %计算FSK信号的幅频特性 m_ContFsk=20*log10(abs(fft(Contfsk,2048))); m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));; m07_ContFsk=m_ContFsk-max(m_ContFsk); m07_DisFsk=m_DisFsk-max(m_DisFsk); %仿真调制指数为0.715时的FSK信号 m=1; %调制指数 freqsep=m*ps; %FSK信号中，两个频率之间的间隔 nsamp=Fs/ps; %每个码元的采样点数 x = randint(N,1,2); % 产生随机数据做为数据码元 ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont'); % 产生连续相位FSK调制信号的正交基带数据 DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据 %将基带FSK信号正交上变频至6MHz中频 t=0:1/Fs:(Len-1)/Fs; f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1); Contfsk=real(ContData.*f0'); DisContfsk=real(DisContData.*f0'); %计算FSK信号的幅频特性 m_ContFsk=20*log10(abs(fft(Contfsk,2048))); m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));; m1_ContFsk=m_ContFsk-max(m_ContFsk); m1_DisFsk=m_DisFsk-max(m_DisFsk); %仿真调制指数为3.5时的FSK信号 m=3.5; %调制指数 freqsep=m*ps; %FSK信号中，两个频率之间的间隔 nsamp=Fs/ps; %每个码元的采样点数 x = randint(N,1,2); % 产生随机数据做为数据码元 ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont'); % 产生连续相位FSK调制信号的正交基带数据 DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据 %将基带FSK信号正交上变频至6MHz中频 t=0:1/Fs:(Len-1)/Fs; f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1); Contfsk=real(ContData.*f0'); DisContfsk=real(DisContData.*f0'); %计算FSK信号的幅频特性 m_ContFsk=20*log10(abs(fft(Contfsk,2048))); m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));; m35_ContFsk=m_ContFsk-max(m_ContFsk); m35_DisFsk=m_DisFsk-max(m_DisFsk); %绘图 %设置幅频响应的横坐标单位为MHz x_f=1:length(m_ContFsk);x_f=x_f*Fs/length(m_ContFsk)/10^6; %绘制连续相位的时域波形及频谱 figure(1); subplot(421); plot(x_f,m05_ContFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=0.5 CPFSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(422); plot(x_f,m05_DisFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=0.5 FSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(423); plot(x_f,m07_ContFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=0.715 CPFSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(424); plot(x_f,m07_DisFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=0.715 FSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(425); plot(x_f,m1_ContFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=1 CPFSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(426); plot(x_f,m1_DisFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=1 FSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(427); plot(x_f,m35_ContFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=3.5 CPFSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(428); plot(x_f,m35_DisFsk);axis([0 Fs/2/10^6 -80 0]); legend('h=3.5 FSK'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; 

2.2非相干解调FSK

参数要求：解调非连续相位和连续相位的2FSK调制信号；仿真调制度分别为0.5、3.5的2FSK调制信号；基带信号符号速率Rb=1Mbps；载波频率fc=6MHz;采样频率fs=32Rb；

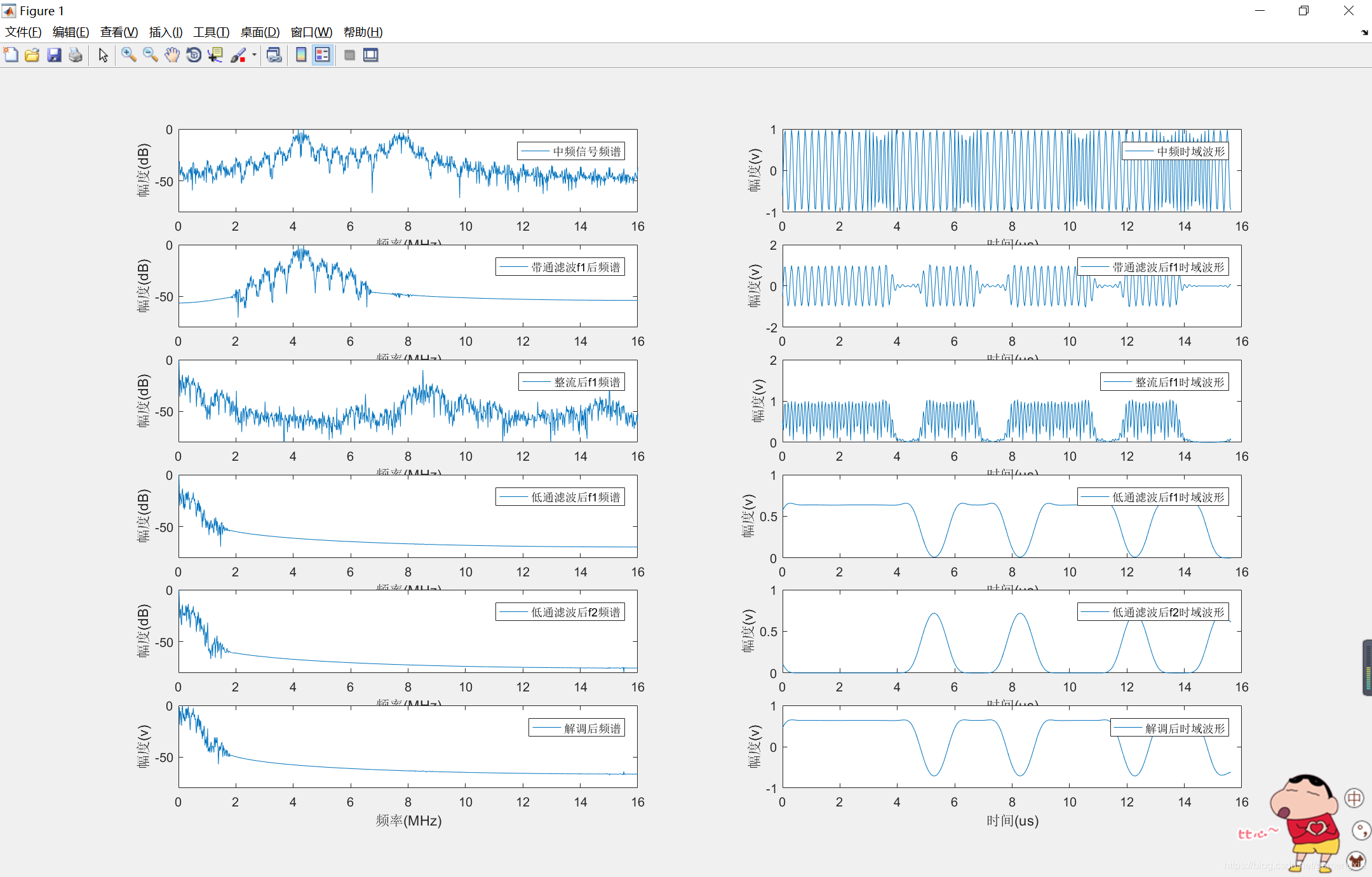
m=3.5; %调制度为3.5 IsCont=1; %CPFSK ps=1*10^6; %码速率为1MHz N=1000; %数据码元个数 Fs=32*10^6; %采样速率为32MHz fc=6*10^6; %载波频率为6MHz Len=N*Fs/ps; %仿真调制指数为3.5时的FSK信号 freqsep=m*ps; %FSK信号中，两个频率之间的间隔 nsamp=Fs/ps; %每个码元的采样点数 x = randint(N,1,2); % 产生随机数据做为数据码元 if IsCont==1 fsk = fskmod(x,2,freqsep,nsamp,Fs,'cont'); % 产生连续相位FSK调制信号的正交基带数据 else fsk = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据 end %将基带FSK信号正交上变频至6MHz中频 t=0:1/Fs:(Len-1)/Fs; f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1); fsk=real(fsk.*f0'); %计算FSK信号的幅频特性 m_fsk=20*log10(abs(fft(fsk,2048))); m0_fsk=m_fsk-max(m_fsk); %对FSK信号进行带通滤波 Wnf1=[(fc-m*ps)*2/Fs fc*2/Fs]; Wnf2=[fc*2/Fs (fc+m*ps)*2/Fs]; b1=fir1(60,Wnf1); b2=fir1(60,Wnf2); bs1_fsk=filter(b1,1,fsk); bs2_fsk=filter(b2,1,fsk); %计算带通滤波后的幅频特性 m_fsk=20*log10(abs(fft(bs1_fsk,2048))); mbs1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(bs2_fsk,2048))); mbs2_fsk=m_fsk-max(m_fsk); %对带通滤波后的数据进行全波整流 abs1_fsk=abs(bs1_fsk); abs2_fsk=abs(bs2_fsk); %计算整流后的幅频特性 m_fsk=20*log10(abs(fft(abs1_fsk,2048))); mabs1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(abs2_fsk,2048))); mabs2_fsk=m_fsk-max(m_fsk); %对整流后的数据进行低通滤波 Lb=fir1(60,ps*2/Fs); Lpf1_fsk=filter(Lb,1,abs1_fsk); Lpf2_fsk=filter(Lb,1,abs2_fsk); %计算低通滤波后的幅频特性 m_fsk=20*log10(abs(fft(Lpf1_fsk,2048))); mLpf1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(Lpf2_fsk,2048))); mLpf2_fsk=m_fsk-max(m_fsk); %对低通滤波后的两路信号相减，形成基带信号波形 Demod_fsk=Lpf1_fsk-Lpf2_fsk; %计算解调后的基带信号幅频特性 m_fsk=20*log10(abs(fft(Demod_fsk,2048))); mDemod_fsk=m_fsk-max(m_fsk); %绘图 %设置幅频响应的横坐标单位为MHz x_f=1:length(m0_fsk);x_f=x_f*Fs/length(m0_fsk)/10^6; %绘制连续相位的时域波形及频谱 figure(1); subplot(621); plot(x_f,m0_fsk);axis([0 Fs/2/10^6 -80 0]); legend('中频信号频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(622); plot([0:1/32:500/32],fsk(100:600)); legend('中频时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(623); plot(x_f,mbs1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('带通滤波f1后频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(624); plot([0:1/32:500/32],bs1_fsk(100:600)); legend('带通滤波后f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(625); plot(x_f,mabs1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('整流后f1频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(626); plot([0:1/32:500/32],abs1_fsk(100:600)); legend('整流后f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(627); plot(x_f,mLpf1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('低通滤波后f1频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(628); plot([0:1/32:500/32],Lpf1_fsk(100:600)); legend('低通滤波后f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(629); plot(x_f,mLpf2_fsk);axis([0 Fs/2/10^6 -80 0]); legend('低通滤波后f2频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(6,2,10); plot([0:1/32:500/32],Lpf2_fsk(100:600)); legend('低通滤波后f2时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(6,2,11); plot(x_f,mDemod_fsk);axis([0 Fs/2/10^6 -80 0]); legend('解调后频谱'); xlabel('频率(MHz)');ylabel('幅度(v)');%grid on; subplot(6,2,12); plot([0:1/32:500/32],Demod_fsk(100:600)); legend('解调后时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; 

2.2相干解调FSK仿真

参数要求：解调非连续相位的2FSK调制信号；仿真调制度分别为0.5、3.5的2FSK调制信号；基带信号符号速率Rb=1Mbps；载波频率fc=6MHz；采样频率fs=32Rb；

m=3.5; %调制度为3.5 ps=1*10^6; %码速率为1MHz N=1000; %数据码元个数 Fs=32*10^6; %采样速率为32MHz fc=6*10^6; %载波频率为6MHz Len=N*Fs/ps; t=0:1/Fs:(Len-1)/Fs; f1=cos(2*pi*(fc-m*ps/2).*t)';%FSK信号中两种码元所代表的频率 f2=cos(2*pi*(fc+m*ps/2).*t)'; %根据式（6-1）产生非连续相位FSK信号 x = randint(N,1,2); % 产生随机数据做为数据码元 dx=rectpulse(x,Fs/ps); % 对随机数据进行Fs/ps倍采样 fsk=dx.*f1+(~dx).*f2; %计算FSK信号的幅频特性 m_fsk=20*log10(abs(fft(fsk,2048))); m0_fsk=m_fsk-max(m_fsk); %对FSK信号进行带通滤波 Wnf1=[(fc-m*ps)*2/Fs fc*2/Fs]; Wnf2=[fc*2/Fs (fc+m*ps)*2/Fs]; b1=fir1(60,Wnf1); b2=fir1(60,Wnf2); bs1_fsk=filter(b1,1,fsk); bs2_fsk=filter(b2,1,fsk); %计算带通滤波后的幅频特性 m_fsk=20*log10(abs(fft(bs1_fsk,2048))); mbs1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(bs2_fsk,2048))); mbs2_fsk=m_fsk-max(m_fsk); %为仿真相干载波，需要对f1、f2也进行带波滤波的延时处理 f1=filter(b1,1,f1); f2=filter(b2,1,f2); %乘以相干载波 cf1_fsk=bs1_fsk.*f1; cf2_fsk=bs2_fsk.*f2; %计算乘以相干载波后的幅频特性 m_fsk=20*log10(abs(fft(cf1_fsk,2048))); mcf1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(cf2_fsk,2048))); mcf2_fsk=m_fsk-max(m_fsk); %对乘法运算后的数据进行低通滤波 Lb=fir1(60,ps*2/Fs); Lpf1_fsk=filter(Lb,1,cf1_fsk); Lpf2_fsk=filter(Lb,1,cf2_fsk); %计算低通滤波后的幅频特性 m_fsk=20*log10(abs(fft(Lpf1_fsk,2048))); mLpf1_fsk=m_fsk-max(m_fsk); m_fsk=20*log10(abs(fft(Lpf2_fsk,2048))); mLpf2_fsk=m_fsk-max(m_fsk); %对低通滤波后的两路信号相减，形成基带信号波形 Demod_fsk=Lpf1_fsk-Lpf2_fsk; %计算解调后的基带信号幅频特性 m_fsk=20*log10(abs(fft(Demod_fsk,2048))); mDemod_fsk=m_fsk-max(m_fsk); %绘图 %设置幅频响应的横坐标单位为MHz x_f=1:length(m0_fsk);x_f=x_f*Fs/length(m0_fsk)/10^6; %绘制连续相位的时域波形及频谱 figure(1); subplot(621); plot(x_f,m0_fsk);axis([0 Fs/2/10^6 -80 0]); legend('中频信号频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(622); plot([0:1/32:500/32],fsk(100:600)); legend('中频时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(623); plot(x_f,mbs1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('带通滤波f1后频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(624); plot([0:1/32:500/32],bs1_fsk(100:600)); legend('带通滤波后f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(625); plot(x_f,mcf1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('乘以相干载波f1频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(626); plot([0:1/32:500/32],cf1_fsk(100:600)); legend('乘以相干载波f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(627); plot(x_f,mLpf1_fsk);axis([0 Fs/2/10^6 -80 0]); legend('低通滤波后f1频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(628); plot([0:1/32:500/32],Lpf1_fsk(100:600)); legend('低通滤波后f1时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(629); plot(x_f,mLpf2_fsk);axis([0 Fs/2/10^6 -80 0]); legend('低通滤波后f2频谱'); xlabel('频率(MHz)');ylabel('幅度(dB)');%grid on; subplot(6,2,10); plot([0:1/32:500/32],Lpf2_fsk(100:600)); legend('低通滤波后f2时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on; subplot(6,2,11); plot(x_f,mDemod_fsk);axis([0 Fs/2/10^6 -80 0]); legend('解调后频谱'); xlabel('频率(MHz)');ylabel('幅度(v)');%grid on; subplot(6,2,12); plot([0:1/32:500/32],Demod_fsk(100:600)); legend('解调后时域波形'); xlabel('时间(us)');ylabel('幅度(v)');%grid on;