大家好,欢迎来到IT知识分享网。
一、线性规划求解
在上一篇博客 【运筹学】线性规划数学模型 ( 求解基矩阵示例 | 矩阵的可逆性 | 线性规划表示为 基矩阵 基向量 非基矩阵 非基向量 形式 ) 中 , 将线性规划的等式表示为以下形式 :
B X B + N X N = b BX_B + NX_N = b BXB+NXN=b
写成上述形式之后 , 就可以表示出上述等式的解 , 如果上述等式解满足线性规划约束变量的要求 , 即所有的变量都大于等于 0 , 那么该解就是线性规划的解 ;
上述式子中 , X N X_N XN 非基变量 , 是可以随意取值的变量 ;
只要非基变量 X N X_N XN 取定一组解 , 基变量 X B X_B XB 就可以被唯一确定 ;
( X B X N ) \begin{pmatrix} X_B \\ X_N \\ \end{pmatrix} (XBXN) 就是 方程组完整的解 ;
二、根据非基变量的解得到基变量解
如何根据非基变量 X N X_N XN 的解 , 确定基变量 X B X_B XB 的解 ?
基矩阵 B B B 是可逆的 , 那么 B B B 的逆矩阵 B − 1 B^{-1} B−1 是存在的 , 上述方程 B X B + N X N = b BX_B + NX_N = b BXB+NXN=b 左右两端 , 都乘以 B − 1 B^{-1} B−1 , 如下计算 :
B X B + N X N = b ( B X B + N X N ) × B − 1 = B − 1 b I × X B + B − 1 N X N = B − 1 b X B = B − 1 b − B − 1 N X N \begin{array}{lcl} BX_B + NX_N &=& b\\\\ ( BX_B + NX_N ) \times B^{-1} &=& B^{-1}b \\\\ I \times X_B + B^{-1}NX_N &=& B^{-1}b\\\\ X_B & = & B^{-1}b – B^{-1}NX_N \end{array} BXB+NXN(BXB+NXN)×B−1I×XB+B−1NXNXB====bB−1bB−1bB−1b−B−1NXN
其中 I I I 是单位阵 , 单位阵乘以矩阵 X B X_B XB 其结果还是 X B X_B XB ;
关于单位阵 , 参考 单位矩阵 – 百度百科
上述式子最终得到 X B = B − 1 b − B − 1 N X N X_B = B^{-1}b – B^{-1}NX_N XB=B−1b−B−1NXN , 此时 如果非基变量的值 X N X_N XN 已经解出来 , 那么 基变量 X B X_B XB 可以通过上述表达式表示出来 ;
三、基解
给定一个基矩阵 B B B , 约束方程可以转化成 X B = B − 1 b − B − 1 N X N X_B = B^{-1}b – B^{-1}NX_N XB=B−1b−B−1NXN 形式 , 只要给定一组 X N X_N XN 的解 , 就可以 得到一组 X B X_B XB 的解 ;
非基变量 O O O 解 : 找到 X N X_N XN 的一组最简单的解 , 这里随意找一组 X N X_N XN 的解都可以 , 最简单的一组解就是 X N X_N XN 的所有值都是 0 0 0 , 即让所有的非基变量等于 0 0 0 , 此时 X N X_N XN 为零矩阵 , 使用 O O O 表示 ;
对应基变量的解 : 将所有的非基变量等于 0 0 0 , 即 X N = O X_N = O XN=O 的条件代入 X B = B − 1 b − B − 1 N X N X_B = B^{-1}b – B^{-1}NX_N XB=B−1b−B−1NXN 中 , 有 :
X B = B − 1 b X_B = B^{-1}b XB=B−1b
此时线性规划的解为 : ( B − 1 b O ) \begin{pmatrix} B^{-1}b \\ O \\ \end{pmatrix} (B−1bO) , 其中 O O O 是零矩阵 ; 该解就是线性规划的基解 ;
基矩阵 B B B -> 非基变量解 O O O -> 基变量解 B − 1 b B^{-1}b B−1b : 基解最根本是先确定基矩阵 B B B , 确定 基矩阵 B B B 之后 , 就可以将变量分为基变量 和 非基变量 , 此时将非基变量取值为零矩阵 O O O , 得到基变量的解 B − 1 b B^{-1}b B−1b ;
基解 X B X_B XB 是由基矩阵 B B B 唯一确定的 ; 只要给定基矩阵 , 就可以唯一确定基解 ;
基解个数 : 一个线性规划中的基解个数 , 就是基矩阵可数 , 就是可逆矩阵个数 ;
通常情况下的基解个数 : 系数矩阵 A A A , 是 m × n m \times n m×n 维的矩阵 , m m m 行等式 , n n n 个变量 , 其任意 m m m 列向量 , 组成的 m m m 阶方阵 , 都是可逆矩阵 , 其有 C ( n , m ) C(n,m) C(n,m) 个基矩阵 , 也有 C ( n , m ) C(n,m) C(n,m) 组基解 ;
基解定义 : 确定一个 m × n m \times n m×n 阶系数矩阵的基矩阵 B B B , 令非基变量 X N X_N XN 等于 0 0 0 , 有约束条件 X B = B − 1 b − B − 1 N X N X_B = B^{-1}b – B^{-1}NX_N XB=B−1b−B−1NXN 可以解出其基变量 X B X_B XB , 这组 ( B − 1 b O ) \begin{pmatrix} B^{-1}b \\ O \\ \end{pmatrix} (B−1bO) 解 , 称为基解 ; 基解中的变量取非 0 0 0 值的个数 , 不超过等式个数 m m m , 基解总数不超过 C ( n , m ) C(n,m) C(n,m) ;
四、基可行解
完整的线性规划标准形式如下 :
m a x Z = ∑ j = 1 n c j x j s . t { ∑ j = 1 n a i j x j = b i i = 1 , 2 , ⋯ , m x j ≥ 0 j = 1 , 2 , ⋯ , n \begin{array}{lcl}max Z = \sum_{j = 1}^{n} c_j x_j\\\\ s.t \begin{cases} \sum_{j = 1}^{n} a_{ij} x_j = b_i & i = 1,2,\cdots,m \\ \\ x_j \geq 0 & j= 1, 2,\cdots,n \end{cases}\end{array} maxZ=∑j=1ncjxjs.t⎩⎪⎨⎪⎧∑j=1naijxj=bixj≥0i=1,2,⋯,mj=1,2,⋯,n
上述的基解 , 只是根据 ∑ j = 1 n a i j x j = b i ( i = 1 , 2 , ⋯ , m ) \sum_{j = 1}^{n} a_{ij} x_j = b_i \quad ( i = 1,2,\cdots,m) ∑j=1naijxj=bi(i=1,2,⋯,m) 约束条件等式解出的 ;
还需要满足 x j ≥ 0 ( j = 1 , 2 , ⋯ , n ) x_j \geq 0 \quad ( j= 1, 2,\cdots,n) xj≥0(j=1,2,⋯,n) 条件 ;
基可行解定义 : 满足线性规划中的 x j ≥ 0 ( j = 1 , 2 , ⋯ , n ) x_j \geq 0 \quad ( j= 1, 2,\cdots,n) xj≥0(j=1,2,⋯,n) 约束条件的 基解 , 称为 基可行解 ;
给定线性规划系数矩阵 m × n m \times n m×n 阶 :
- 其可行解个数是无限的 , 因为其非基变量 X N X_N XN 可以有无限种取值 , 对应的基变量 X B X_B XB 也有无限种取值 ;
- 其基解个数是有限的 , 因为非基变量只能取 O O O 零矩阵 , 对应的基变量也是有限的 , 不超过 C n m C_n^m Cnm 个 ;
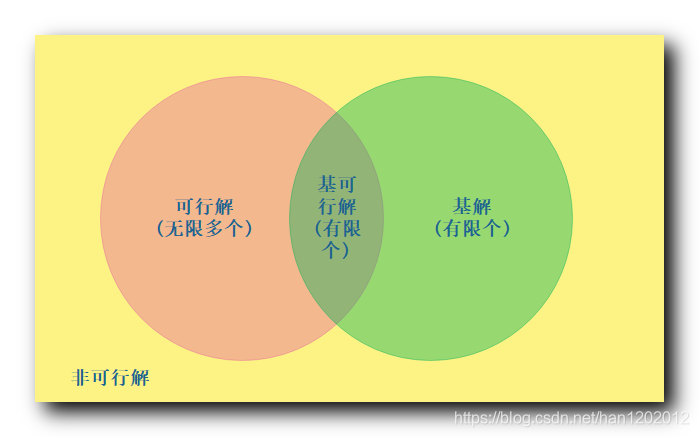
可行解有无穷多个 , 基解是有限个 , 如果一个解既是基解 , 又是可行解 , 那么称该解是基可行解 ;
基解个数是有限的 , 基可行解 是 基解 与 可行解 的交集 , 基可行解的个数必然也是有限的 ;
迭代思想 : 在解里面找到一个解 , 看该解是否是最优的 , 如果不是 , 就迭代到下一个解 , 继续重复查看该解是否是最优 ; 如果迭代的集合是有限的 , 其肯定要比无限的集合简单很多 ;
因此线性规划中 , 在有限个基可行解中 , 迭代查找最优解 , 将搜索范围从无限个可行解 , 变成了有限个基可行解 ;
五、可行基
可行基 : 基可行解 对应的 基矩阵 B B B , 就是 可行基 ;
使用 X B = B − 1 b − B − 1 N X N X_B = B^{-1}b – B^{-1}NX_N XB=B−1b−B−1NXN , 代入 X N = O X_N = O XN=O , 解出其基变量 X B X_B XB , 这组 ( B − 1 b O ) \begin{pmatrix} B^{-1}b \\ O \\ \end{pmatrix} (B−1bO) 基解 , X N X_N XN 中的非基变量解肯定是大于等于 0 0 0 的 , 如果 B − 1 b B^{-1}b B−1b 中有负分量 , 那么该解不是基可行解 , 对应的基矩阵 X B X_B XB 不是可行基 ;
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/127944.html