动态规划——最长上升子序列模型

大家好，欢迎来到IT知识分享网。

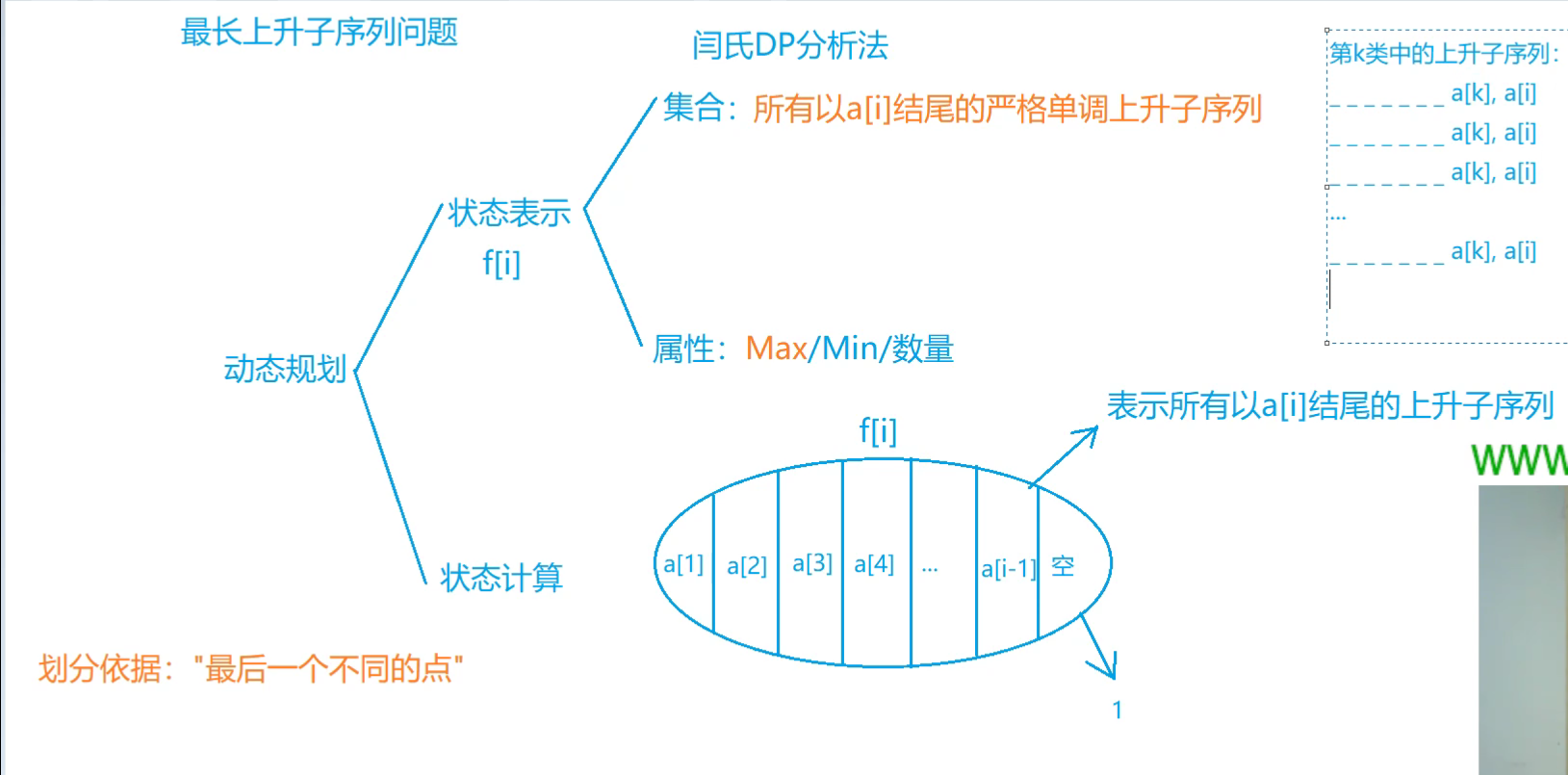
母题1：最长上升子序列

$$状态表示f[i]：\{\begin{array}{l}集合：所有以第i个数结尾的上升子序列\\ 属性：子序列长度的\mathrm{Max}\end{array}$$

状态计算：看第 $i-1$ 个数选的是原序列的第 $1,2,\dots$ 个数，在a[j] < a[i]时，有f[i] = max(f[i], f[j] + 1)，$j=1,2,3\dots i-1$

边界：若没有 $i-1$（没有比第 $i$ 个数小的）则f[i] = 1 （以自己为结尾的子序列）

#include <bits/stdc++.h> using namespace std; const int N = 1010; int a[N], f[N], n; int main() { 
    cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) { 
    f[i] = 1;//长度至少为1 for (int j = 1; j < i; j++) if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1); } //现在f[i]表示以第i个数结尾的最长上升子序列长度，再对所有f[i]取一遍max int res = 0; for (int i = 1; i <= n; i++) res = max(res, f[i]); cout << res; return 0; } 

另外一种写法：

#include <bits/stdc++.h> using namespace std; const int N = 1010; int a[N], f[N], n, res; int main() { 
    cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) { 
    f[i] = 1; for (int j = 1; j < i; j++) if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1); res = max(res, f[i]); } cout << res; return 0; } 

若要存储最长的上升子序列并将其输出，可记录状态的转移：

#include <bits/stdc++.h> using namespace std; const int N = 1010; int a[N], f[N], g[N], n, res; int main() { 
    cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) { 
    f[i] = 1; g[i] = 0;//g[]记录状态是从哪转移的，初始时记为0 for (int j = 1; j < i; j++) { 
    if (a[j] < a[i]) { 
    if (f[i] < f[j] + 1) { 
    f[i] = f[j] + 1; g[i] = j;//表示第i个元素是从a[j]转移来的 } } } } int k = 1; for (int i = 1; i <= n; i++) { 
    if (f[k] < f[i]) k = i;//求出f[]中的最大值 } res = f[k]; cout << res << "\n";//f[k]就是最长上升子序列的长度 while (k) { 
    cout << a[k] << " "; k = g[k]; }//这样会逆着输出最长上升的子序列，如果要倒序的话再逆序一下即可 return 0; } 

以上代码会在输入为

7 3 1 2 1 8 5 6 

的情况下输出

4 6 5 2 1 

母题2：最长上升子序列 II

本题的数据范围是 $10^5$，如仍使用 $dp$ 会导致 $\mathsf{TLE}$，因此需要优化。

贪心 + 二分

#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; int a[N], n; int main() { 
    cin >> n; for (int i = 0; i < n; i++) cin >> a[i]; vector<int> v; v.push_back(a[0]); for (int i = 1; i < n; i++) { 
    if (a[i] > v.back()) v.push_back(a[i]);//如果该元素大于栈顶元素,将该元素入栈 else *lower_bound(v.begin(), v.end(), a[i]) = a[i];//替换掉第一个大于或者等于这个数字的那个数 } cout << v.size(); return 0; } 

注意得用lower_bound而非upper_bound。数列严格递增，假如是1 2 3，再加上两个1，upper_bound会更改成1 1 1，只能保证数列单调不减。

栈中序列虽然递增，但是每个元素在原串中对应的位置其实可能是乱的，那为什么这个栈还能用于计算最长子序列长度？
实际上这个栈并不用于记录最终的最长子序列，而是【以v[i]结尾的子串长度最长为i】或者说【长度为i的递增子串中，末尾元素最小的是v[i]】。理解了这个问题以后就知道为什么新进来的元素要不就在末尾增加，要不就替代第一个大于等于它元素的位置。
这里的【替换】就蕴含了一个贪心的思想，对于同样长度的子串，我当然希望它的末端越小越好，这样以后我也有更多机会拓展。

母题3：最长公共子序列

$$状态表示f[i,j]：\{\begin{array}{l}集合：所有在第一个序列的前i个字母中出现，且在第二个序列的前j个字母中出现的子序列\\ 属性：子序列长度的\mathrm{Max}\end{array}$$

状态计算：依据a[i]和b[j]是否在公共子序列中，共有4种情况（4个子集）：
①$00$：a[i]和b[j]都不在
即在第一个序列的前 $i-1$ 个字母中出现，且在第二个序列的前 $j-1$ 个字母中出现的子序列 $⟹$ f[i-1][j-1]

②$01$：a[i]不在，b[j]在
值得注意的是，该子集 $\in$ f[i-1][j]，而非等价。f[i-1][j]表示在第一个序列的前 $i-1$ 个字母中出现，且在第二个序列的前 $j$ 个字母中出现的子序列，其中未必一定有 b[j]，所以其还包含了 $00$ 这一子集，即f[i-1][j-1] $\in$ f[i-1][j]。但就本题而言，属性是$\mathrm{Max}$，集合划分只需“不漏”即可，允许各子集之间有重复，因为并集不改变最大值

③$10$：a[i]在，b[j]不在
与上面的分析类似，该子集 $\in$ f[i][j-1]，f[i-1][j-1] $\in$ f[i][j-1]。

④$11$：a[i]和b[j]都在
$⟹$ f[i-1][j-1] + 1
值得注意的是，这种情况仅在a[i] == b[j]时才存在。

由于f[i-1][j-1]已经包含在f[i-1][j]和f[i][j-1]中，我们最后只需将f[i-1][j]，f[i][j-1]，f[i-1][j-1]+1 三者取 $\mathrm{Max}$ 即可。

#include <bits/stdc++.h> using namespace std; const int N = 1010; int f[N][N], n, m; char a[N], b[N]; int main() { 
    cin >> n >> m; cin >> a + 1 >> b + 1;//由于涉及到i-1和j-1，下标一律从1开始 for (int i = 1; i <= n; i++) { 
    for (int j = 1; j <= m; j++) { 
    f[i][j] = max(f[i - 1][j], f[i][j - 1]); if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1); } } cout << f[n][m]; return 0; } 

母题4：最长公共子序列 II

本题数据范围为 $10^5$ 会卡掉 $O(n^2)$ 的算法，因此上一题的算法需要再优化。

注意到两个序列都是 $1$ 到 $n$ 的全排列，那么两个序列元素互异且相同，也就是说只是位置不同罢了，那么我们可以通过一个 $\mathrm{map}$ 数组将 $A$ 序列的数字在 $B$ 序列中的位置表示出来。

示例：

A:3 2 1 4 5 B:1 2 3 4 5 

我们不妨给它们重新标个号：把 $3$ 标成 $a$, 把 $2$ 标成 $b$，把 $1$ 标成 $c$ ……于是变成：

A: a b c d e B: c b a d e 

这样标号之后，$\mathrm{LCS}$ 长度显然不会改变。但是出现了一个性质：

两个序列的子序列，一定是 $A$ 的子序列。而 $A$ 本身就是单调递增的。
因此这个子序列是单调递增的。

换句话说，只要这个子序列在 $B$ 中单调递增，它就是 $A$ 的子序列。

哪个最长呢？当然是 $B$ 的 $\mathrm{LIS}$ 最长。

自此完成转化。

#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; int a[N], b[N], n, g[N]; map<int, int> mp; int main() { 
    scanf("%d", &n); for (int i = 1; i <= n; i++) { 
    scanf("%d", &a[i]); mp[a[i]] = i; } for (int i = 1; i <= n; i++) { 
    scanf("%d", &b[i]); b[i] = mp[b[i]]; } g[1] = b[1]; int k = 1; for (int i = 2; i <= n; i++) { 
    if (g[k] < b[i]) g[++k] = b[i]; else *lower_bound(g + 1, g + k + 1, b[i]) = b[i]; } printf("%d", k); } 

子题1：怪盗基德的滑翔翼

本题对于每一个数组元素a[i]，计算以其为结尾的最长上升子序列和以其为开始的最长下降子序列长度之和即为所求。所以只需先从前到后再从后到前计算两次最长上升子序列即可。

#include <cstdio> #include <algorithm> const int N = 110; int a[N], f[N]; int main() { 
    int K; scanf("%d", &K); while (K--) { 
    int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); int res = 0; for (int i = 1; i <= n; i++) { 
    f[i] = 1; for (int j = 1; j < i; j++) { 
    if (a[i] > a[j]) f[i] = std::max(f[i], f[j] + 1); } res = std::max(res, f[i]); } for (int i = n; i >= 1; i--) { 
    f[i] = 1; for (int j = n; j > i; j--) { 
    if (a[i] > a[j]) f[i] = std::max(f[i], f[j] + 1); } res = std::max(res, f[i]); } printf("%d\n", res); } return 0; } 

子题2：登山

1、按照编号的递增顺序来浏览 $⟹$ 必须是子序列
2、相邻两个结点不能相同 $⟹$ 严格单调
3、一旦开始下降就不能上升了 $⟹$ 登山队员 的行动曲线为一条折线：先向上再向下。

本题相较于上一题的区别是，上一题是对于每一个数组元素，可以向左也可以向右，将二者取 $\max$；而本题是强制必须既向左又向右，取和为折线的长度，最后将所有折线的长度取 $\max$。

本题如果枚举每一个数组元素再计算以其为结尾和起点的最长上升/下降子序列长度的话时间复杂度为 $O(n^3)$ 会超时，因此考虑先预处理出每个数组元素对应的折线长度，最后再枚举数组元素取 $\max$，这样的时间复杂度为 $O(n^2)$。

#include <cstdio> #include <algorithm> const int N = 1010; int a[N], f[N], g[N];//f[i]记录以a[i]为结尾的上升子序列的最大长度，g[i]记录以a[i]为起点的下降子序列的最大长度。 int main() { 
    int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); for (int i = 1; i <= n; i++) { 
    f[i] = 1; for (int j = 1; j < i; j++) { 
    if (a[i] > a[j]) f[i] = std::max(f[i], f[j] + 1); } } for (int i = n; i >= 1; i--) { 
    g[i] = 1; for (int j = n; j > i; j--) { 
    if (a[i] > a[j]) g[i] = std::max(g[i], g[j] + 1); } } int res = 0; for (int i = 1; i <= n; i++) res = std::max(res, f[i] + g[i] - 1);//f[i]和g[i]所记录的序列长度均包含了a[i]这个元素（长度为1），因此要减去。 printf("%d", res); return 0; } 

子题3：合唱队形

和上一题登山简直一模一样（只需把输出改成n - res即可）

#include <cstdio> #include <algorithm> const int N = 110; int a[N], f[N], g[N]; int main() { 
    int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); for (int i = 1; i <= n; i++) { 
    f[i] = 1; for (int j = 1; j < i; j++) { 
    if (a[i] > a[j]) f[i] = std::max(f[i], f[j] + 1); } } for (int i = n; i >= 1; i--) { 
    g[i] = 1; for (int j = n; j > i; j--) { 
    if (a[i] > a[j]) g[i] = std::max(g[i], g[j] + 1); } } int res = 0; for (int i = 1; i <= n; i++) res = std::max(res, f[i] + g[i] - 1); printf("%d", n - res); return 0; } 

子题4：友好城市

首先可以想到用 $\mathrm{pair}$ 存城市的坐标信息。我们可以对 $\mathrm{pair}$ 的任意一个关键字排序，由于要求桥之间不能相交，则另一个关键字也必须有序，即如果出现逆序则必相交。则一个合法的建桥方式对应一个上升的子序列。目标转化为求解最长上升子序列的长度。

#include <bits/stdc++.h> const int N = 5010; std::pair<int, int> q[N]; int f[N]; int main() { 
    int n; scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%d%d", &q[i].first, &q[i].second); std::sort(q, q + n); int res = 0; for (int i = 0; i < n; i++) { 
    f[i] = 1; for (int j = 0; j < i; j++) { 
    if (q[i].second > q[j].second) f[i] = std::max(f[i], f[j] + 1); } res = std::max(res, f[i]); } printf("%d", res); return 0; } 

子题5：最大上升子序列和

和最长上升子序列很相似，只需稍微更改一下状态转移方程即可。

#include <bits/stdc++.h> const int N = 1010; int a[N], f[N]; int main() { 
    int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); int res = 0; for (int i = 1; i <= n; i++) { 
    f[i] = a[i]; for (int j = 1; j < i; j++) { 
    if (a[j] < a[i]) f[i] = std::max(f[i], f[j] + a[i]); } res = std::max(res, f[i]); } printf("%d", res); return 0; } 

子题6：导弹拦截

题目简化：

给定一个数列 $a$，
1、求解其最长不上升子序列长度
2、最少能被划分成多少个不上升子序列。

思路讲解：

• 一、为什么要求最长不上升子序列

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

• 二、为什么要求最长上升子序列
  Dilworth定理
  

对偏序集 $<A,⩽>$，设 $A$ 中最长链的长度为 $n$，则将 $A$ 中元素分成不相交的反链，反链长度至少是 $n$。

名词解释：

偏序关系：对于集合 $A$ 上的二元关系 $R$，若 $R$ 具有自反性，反对称性，传递性，那么 $R$ 称为 $A$ 的偏序关系，一般记作 $⩽$（注意这里的 $⩽$ 不必是指一般算数意义上的“小于等于”。）。

偏序集：若在集合 $A$ 上给定一个偏序关系 $⩽$，则称集合 $A$ 按偏序关系 $⩽$ 构成一个偏序集合，集合 $A$ 和偏序 $R$ 一起称为偏序集，记作 $<A,⩽>$。

反链：对于偏序集合 $A$，在 $A$ 的一个子集中，如果每两个元素都是无关的，则称这个子集为反链。

综上可简化为：最少的不上升子序列的个数就是最长上升子序列的长度。

代码实现：
若数据范围在 $10^3\sim 10^4$，可以直接 $dp$，代码如下：

#include <cstdio> #include <algorithm> const int N = 1010; int a[N], f[N], g[N], n, ans1, ans2; int main() { 
    while (scanf("%d", &a[n]) != EOF) n++; for (int i = 0; i < n; i++) { 
    f[i] = 1; g[i] = 1; for (int j = 0; j < i; j++) { 
    if (a[j] >= a[i]) f[i] = std::max(f[i], f[j] + 1); else g[i] = std::max(g[i], g[j] + 1); } ans1 = std::max(ans1, f[i]); ans2 = std::max(ans2, g[i]); } printf("%d\n%d", ans1, ans2); return 0; } 

但本题的数据范围为 $10^5$ 级别，$n^2$ 的算法显然会 $\mathsf{TLE}$。

考虑二分优化。
令数组 $f$ 存储最长不上升子序列，$r_1$ 代表 $f$ 的结尾位置，也即最长不上升子序列的长度。
同理数组 $g$ 存储最长上升子序列，$r_2$ 代表 $g$ 的结尾位置，也即最长上升子序列的长度。

考虑原数组的每个数，若 $a_i⩽f_{r1}$，就把 $a_i$ 直接加入到 $f$ 数组，否则在 $f$ 中找到第一个小于 $a_i$ 的数，用 $a_i$ 替代它。

类似的，考虑原数组的每个数，若 $a_i>g_{r2}$，就把 $a_i$ 直接加入到 $g$ 数组，否则在 $g$ 中找到第一个大于等于 $a_i$ 的数，用 $a_i$ 替代它。

#include <iostream> #include <algorithm> const int N = ; int a[N], f[N], g[N]; int r1, r2, n, x; int main() { 
    while (scanf("%d", &x) != EOF) a[++n] = x; f[1] = g[1] = a[1]; r1 = r2 = 1; for (int i = 2; i <= n; i++) { 
    if (f[r1] >= a[i]) f[++r1] = a[i]; else *std::upper_bound(f + 1, f + r1 + 1, a[i], std::greater<int>()) = a[i]; if (g[r2] < a[i]) g[++r2] = a[i]; else *std::lower_bound(g + 1, g + r2 + 1, a[i]) = a[i]; } printf("%d\n%d", r1, r2); return 0; } 

还可以写作如下的形式（贪心）：

#include <bits/stdc++.h> const int N = ; int a[N], f[N], g[N]; int r1, r2, n; int main() { 
    while (std::cin >> a[n]) n++; for (int i = 0; i < n; i++) { 
    int k = 0; while (k < r1 && g[k] >= a[i]) k++; g[k] = a[i]; if (k >= r1) r1 ++; } for (int i = 0; i < n; i++) { 
    int k = 0; while (k < r2 && g[k] < a[i]) k++; g[k] = a[i]; if (k >= r2) r2 ++; } std::cout << r1 << "\n" << r2; return 0; } 

子题7：导弹防御系统

本题的搜索顺序分为两个阶段：
① 从前往后枚举每颗导弹属于某个上升子序列，还是下降子序列
② 如果属于上升子序列，则枚举属于哪个上升子序列（包括新开一个上升子序列）；如果属于下降子序列，可以类似处理。

分别记录当前每个上升子序列的末尾数 $\mathrm{up}[]$，和下降子序列的末尾数 $\mathrm{down}[]$。这样在枚举时可以快速判断当前数是否可以接在某个序列的后面。

注意这里的记录方式和上一题稍有不同：
① 这里是记录每个子序列末尾的数；
② 上一题是记录每种长度的子序列的末尾最小值。

由于 $\mathrm{dfs}$ 搜索成本很高，考虑剪枝。
假设现在要把一个数放入一个上升序列，那么一定是所有能放入的上升序列中，最后一个元素最大的那一个（贪心）。

对于上升子序列而言，我们将当前数接在最大的数后面，一定不会比接在其他数列后面更差。
这是因为处理完当前数后，一定出现一个以当前数结尾的子序列，这是固定不变的，那么此时其他子序列的末尾数越小越好。

注意到按照这种贪心思路，$\mathrm{up}[]$ 数组和 $\mathrm{down}[]$ 数组一定是单调的，因此在遍历时找到第一个满足的序列后就可以直接 break 了。

这里比较容易混淆，在此强调一下：up数组表示所有严格上升子序列的结尾，它本身随下标是非严格单调下降的；
down数组表示所有严格下降子序列的结尾，它本身随下标是非严格单调上升的。

最后还需要考虑如何求最小值。因为 $\mathrm{DFS}$ 和 $\mathrm{BFS}$ 不同，第一次搜索到的节点，不一定是步数最短的节点，所以需要进行额外处理。
一般有两种处理方式：

① 记录全局最小值，不断更新。

#include <bits/stdc++.h> const int N = 55; int up[N], down[N];//up[]和down[]分别表示所有上升子序列的结尾和所有下降子序列的结尾 int n, a[N]; int ans;//全局最小值 void dfs(int u, int su, int sd) { 
   //u为当前枚举到的数，su为当前上升子序列个数，sd为当前下降子序列个数 if (su + sd >= ans) return; if (u == n) { 
    ans = su + sd; return; } //情况1：将当前数放到上升子序列中 int k = 0; while (k < su && up[k] >= a[u]) k++; int t = up[k];//备份（dfs回溯需恢复现场） up[k] = a[u]; if (k < su) dfs(u + 1, su, sd);//未开辟新的上升子序列 else dfs(u + 1, su + 1, sd);//开辟了新的上升子序列 up[k] = t;//恢复现场 //情况2：将当前数放到下降子序列中 k = 0; while (k < sd && down[k] <= a[u]) k++; t = down[k]; down[k] = a[u]; if (k < sd) dfs(u + 1, su, sd);//未开辟新的下降子序列 else dfs(u + 1, su, sd + 1);//开辟了新的下降子序列 down[k] = t; } int main() { 
    while (std::cin >> n, n) { 
    for (int i = 0; i < n; i++) std::cin >> a[i]; ans = n;//每次暴搜之前将ans设为最大值（最坏情况下每个数单独一个序列） dfs(0, 0, 0); std::cout << ans << "\n"; } return 0; } 

② 迭代加深。一般平均答案深度较低时可以采用这种方式。

#include <bits/stdc++.h> const int N = 60; int n; int h[N]; int up[N], down[N]; bool dfs(int depth, int u, int su, int sd) { 
    // 如果上升序列个数 + 下降序列个数 > 总个数是上限，则回溯 if (su + sd > depth) return false; if (u == n) return true; // 枚举放到上升子序列中的情况 bool flag = false; for (int i = 1; i <= su; i++) if (up[i] < h[u]) { 
    int t = up[i]; up[i] = h[u]; if (dfs(depth, u + 1, su, sd)) return true; up[i] = t; flag = true; break; // 注意由上述证明的贪心原理，只要找到第一个可以放的序列，就可以结束循环了 } if (!flag) // 如果不能放到任意一个序列后面，则单开一个新的序列 { 
    up[su + 1] = h[u]; if (dfs(depth, u + 1, su + 1, sd)) return true; } // 枚举放到下降子序列中的情况 flag = false; for (int i = 1; i <= sd; i++) if (down[i] > h[u]) { 
    int t = down[i]; down[i] = h[u]; if (dfs(depth, u + 1, su, sd)) return true; down[i] = t; flag = true; break; // 注意由上述证明的贪心原理，只要找到第一个可以放的序列，就可以结束循环了 } if (!flag) // 如果不能放到任意一个序列后面，则单开一个新的序列 { 
    down[sd + 1] = h[u]; if (dfs(depth, u + 1, su, sd + 1)) return true; } return false; } int main() { 
    while (std::cin >> n, n) { 
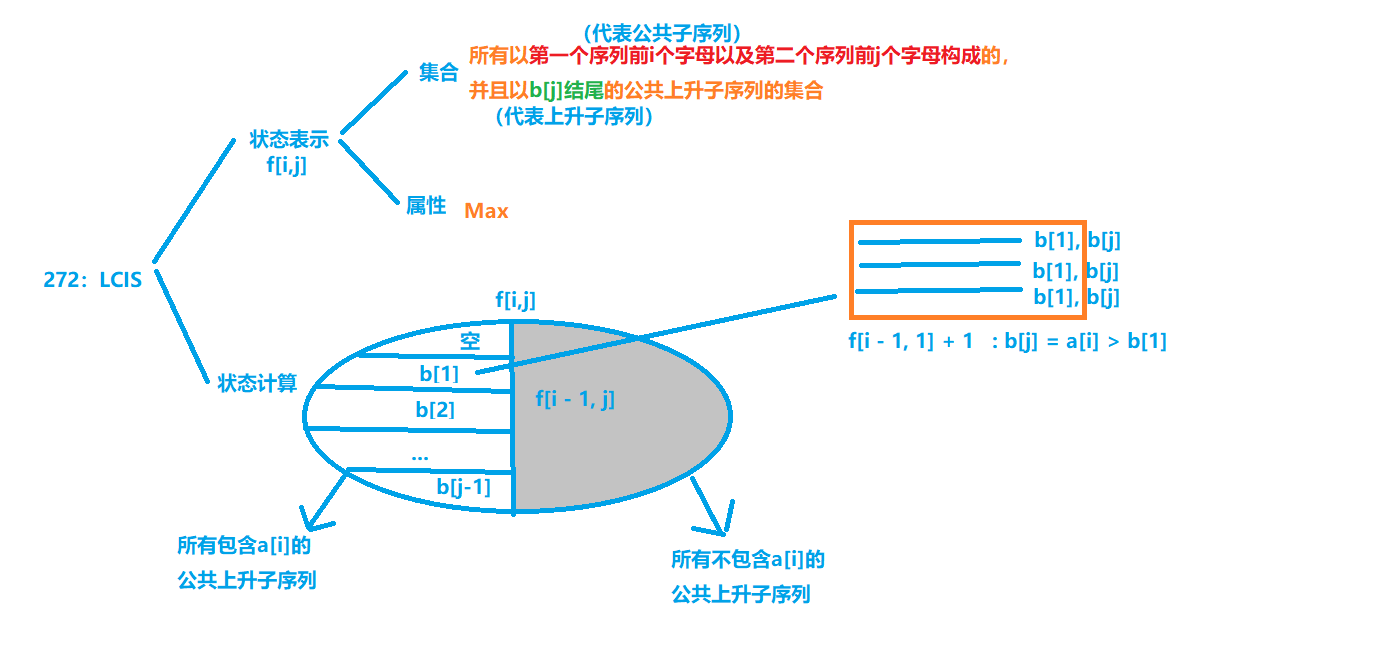
    for (int i = 0; i < n; i ++ ) std::cin >> h[i]; int depth = 0; while (!dfs(depth, 0, 0, 0)) depth++ ; // 迭代加深搜索 std::cout << depth << "\n"; } return 0; } 

子题8：最长公共上升子序列

依据公共子序列中是否包含a[i]，将f[i][j]划分为两个不重不漏的子集：

• 不包含a[i]的子集：最大值为f[i-1][j]
• 包含a[i]的子集：将该子集继续划分，依据是子序列的倒数第二个元素在b[]中是哪个数：
  • 子序列只包含b[j]一个数，长度为 $1$
  • 子序列的倒数第二个数是b[1]的集合，最大长度为f[i-1][1] + 1
  • …
  • 子序列的倒数第二个数是b[j-1]的集合，最大长度为f[i-1][j-1] + 1

如果直接按照上述思路实现，需要三重循环：

for (int i = 1; i <= n; i ++ ) { 
    for (int j = 1; j <= n; j ++ ) { 
    f[i][j] = f[i - 1][j]; if (a[i] == b[j]) { 
    int maxv = 1;//由于a[i] = b[j]，长度至少为1 for (int k = 1; k < j; k ++ ) if (a[i] > b[k]) maxv = max(maxv, f[i - 1][k] + 1); f[i][j] = max(f[i][j], maxv); } } } 

每次循环求得的maxv其实就是满足a[i] > b[k]的f[i-1][k] + 1的前缀最大值，且用到的状态都是第 $i-1$ 阶段的，因此无需再加一重循环，可以直接用一个变量在 $j$ 的循环中同步计算，存储上一个阶段的能够接在a[i]前面的最大的状态值。

最终代码：

#include <cstdio> #include <algorithm> const int N = 3010; int n; int a[N], b[N], f[N][N]; int main() { 
    scanf("%d", &n); for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]); for (int i = 1; i <= n; i ++ ) { 
    int maxv = 1; for (int j = 1; j <= n; j ++ ) { 
    f[i][j] = f[i - 1][j]; if (a[i] == b[j]) f[i][j] = std::max(f[i][j], maxv); if (a[i] > b[j]) maxv = std::max(maxv, f[i - 1][j] + 1); } } int res = 0; for (int i = 1; i <= n; i ++ ) res = std::max(res, f[n][i]); printf("%d\n", res); return 0; }