​光谱优化器（LSO），原理公式详解，附matlab代码

光谱优化器（Light Spectrum Optimizer，LSO)是一种元启发算法，是基于光谱分析的优化算法，它模拟了光谱分析中的频谱分布和峰值搜索过程。该算法通过自适应地调整搜索空间的分辨率和搜索速度，以快速而准确地找到最优解，具有收敛速度快、求解精度高等特点，是一种不错的优化算法。该成果于2022年发表在知名SCI期刊Mathematics上，目前在谷歌学术上被引25次。

LSO算法是一种基于光谱分析的智能优化算法，灵感来自于通过时产生的闪烁彩虹现象，通过模拟光谱分布和峰值搜索过程来寻找最优解。根据笛卡尔定律，当光线从一种材料传播到另一种具有不同折射率的材料时，就会发生折射。这导致白色阳光被分散成七种光谱颜色：红色、橙色、黄色、绿色、蓝色、靛蓝色和紫色，如图所示。

1、算法原理

（1）初始化

LSO的搜索过程从白光初始种群的随机初始化开始，数学表达式为：

其中为初始解，为在[0,1]之间生成的长度等于给定问题维数(d)的均匀随机数向量，lb和ub分别为搜索空间的上界和下界。然后，对生成的初始解决方案进行评估，以确定全局和个人的最佳解决方案。

（2）彩虹光谱的方向

初始化后，内折射法向量、内反射法向量、外折射法向量计算如下:

其中是在迭代时从当前种群中随机选择的解，是在迭代t时的当前解，是迄今为止所找到的全局最佳解，norm(.)表示一个向量的归一化值，根据下面的公式计算:

其中d表示优化问题中的维数。→x是对范数函数进行归一化的输入向量。是输入向量中的JTH维数。对于入射光线，计算如下:

其中是入射光线，是当前总体解

，的平均值， N是种群大小。然后计算内外折射和反射光的矢量为:

其中是在[0,1]之间随机生成的均匀随机数。

（3）产生新的彩色射线

这个阶段有助于将光线分散到迄今为止最佳的解决方案、当前解决方案和从当前人群中随机选择的解决方案，以改进其开发操作符。一开始，算法会将光线分散到当前的解决方案周围，利用它周围的区域来达到更好的结果。然而，这可能会降低的收敛速度，因此，应用附加的步长与预先定义的概率β积分，移动当前的解决方案到目前为止最好的解决方案的方向，以克服这一问题。当前解周围散射的数学模型如下：

其中，是迄今为止最好的解，而和是从当前总体中随机选择的两个解。RV3包括以0和1的间隔随机选择的数字。RVn4是包括在0和1之间随机生成的数的向量。第二散射阶段基于根据以下公式在基于迄今为止的最佳解决方案和当前解决方案的新位置中生成射线：

其中是在0和1的间隔处随机生成的数值。π表示圆的周长与直径之比。第一散射相位和第二散射相位之间的交换基于预定义的概率Pe来实现，如以下公式所示：

其中R是在0和1之间随机生成的数。最后的散射阶段基于根据以下公式根据从总体和当前解决方案中随机选择的解决方案生成新解决方案：

其中RV 5是平均值等于零且标准偏差等于一的正态分布随机数的标量值，并且-U是包括随机值0和1的向量。|…|是绝对值符号，它将负值转换为正值，并返回传递的正数。如果第i条光线的概率适应度值小于R1，则优选地在与迄今为止最佳解相同的方向上散射该光线。我们提出的算法建议这一假设，以最大限度地提高其性能时，处理任何优化问题，需要一个高利用运营商，以加快收敛速度和保存计算成本。

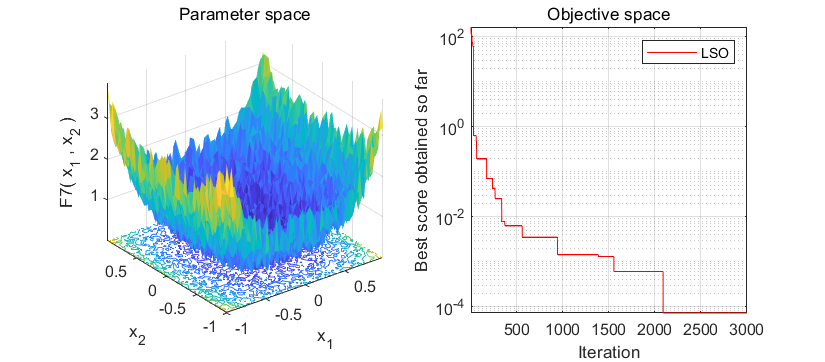
2、结果展示

3、MATLAB核心代码

function [GBest_fitness,GBestRayColor,Conv_curve]=LSO(NoF_LightRays,Max_iter,ub,lb,dim,fobj) %% INITIALIZATION STEP % red=1.3318; violet=1.3435;    % From assumption (2) Conv_curve=zeros(1,Max_iter); % Convergence curve it=1; % Loop counter %% LSO's parameters Ps=0.05; %% Probaility of first and second scattering stages Pe=0.6;  %% Contolling parameter to exchange between the first and second scattering  Ph=0.4;  %% Pobability of Hybridization between two various search boundary methods  B=0.05;  %% Exploitation probability in the first scattering stage % Generate initial population of White Rays for i=1:NoF_LightRays   LightRays(i,:)=lb+(ub-lb).*rand(1,dim);    % Calculate objective function for each search agent   fitness(i)=fobj(LightRays(i,:)); end% initialize Global & Personal best solution [GBest_fitness,index]=min(fitness); GBestRayColor=LightRays(index,:);     NewWLightRays=LightRays; %% Main loop while it<=Max_iter     for i=1:NoF_LightRays        % COLORFUL DISPERSION OF LIGHT RAYS         nA=LightRays(randi(NoF_LightRays),:);                 nB= LightRays(i,:);          nC=GBestRayColor;          xbar=(sum(LightRays)/NoF_LightRays);         norm_nA=nA/norm(nA);   % the normal vector of inner refraction  "equation (6)"         norm_nB=nB/norm(nB);   % the normal vector of inner reflection  "equation (7)"         norm_nC=nC/norm(nC);   % the normal vector of outer refraction  "equation (8)"                Incid_norm=xbar/norm(xbar); % the normal vector of the incident light ray  "equation (11)"         k=red+rand.*(violet-red);      % % Random Refractive Index "equation (15)"         p=rand;          q=rand;          L1=(1./k).*(Incid_norm-(norm_nA.*dot(norm_nA,Incid_norm)))-(norm_nA.*(abs((1-(1./k.^2)+((1./k.^2).*dot(norm_nA,Incid_norm).^2)))).^(1/2)); % "equaton (12)"         L2=L1-((2.*norm_nB).*dot(L1,norm_nB)); % "equation (13)"          L3=k.*(L2-(norm_nC.*dot(norm_nC,L2)))+norm_nC.*(abs(1-(k.^2)+(k.^2).*((dot(norm_nC,L2)).^2))).^(1/2); % "equation (14)"          a=rand*(1-it/Max_iter) ;    % "equation (20)"                  ginv = gammaincinv(a,1); % compute the new ginv value         GI=a*(1/rand)*ginv;   %"equation (19)"         Epsln=a.*randn(1,dim);  %  "equation (18)"          if p<=q             NewWLightRays(i,:)=LightRays(i,:)+GI.*Epsln.*rand(1,dim).*(L1-L3).*(LightRays(randi(NoF_LightRays),:)-LightRays(randi(NoF_LightRays),:));   % "equation (17)"           else             NewWLightRays(i,:)=(LightRays(i,:))+GI.*Epsln.*rand(1,dim).*(L2-L3).*(LightRays(randi(NoF_LightRays),:)-LightRays(randi(NoF_LightRays),:));   % "equation (18)"         end         % % % check bound limitation           if rand<Ph             U=NewWLightRays(i,:)>ub;             L=NewWLightRays(i,:)<lb;             NewWLightRays(i,:)=(NewWLightRays(i,:).*(~(U+L)))+ub.*U+lb.*L;         else             for j=1:size(LightRays,2)                if  NewWLightRays(i,j)>ub(j)                    NewWLightRays(i,j)=lb(j)+rand*(ub(j)-lb(j));                elseif  NewWLightRays(i,j)<lb(j)                    NewWLightRays(i,j)=lb(j)+rand*(ub(j)-lb(j));                end             end          end          % Calculate objective function for each search agent          Fnew=fobj(NewWLightRays(i,:));         % If fitness improves (better solutions found), update then         if (Fnew<=fitness(i))              LightRays(i,:)=NewWLightRays(i,:);              fitness(i)=Fnew;         end      %% update Global best solution         if  Fnew<=GBest_fitness             GBestRayColor=NewWLightRays(i,:);    % Update Global best solution             GBest_fitness=Fnew;         end         [in1]=sort(fitness);         Conv_curve(it)=GBest_fitness;         it=it+1;         if (it>Max_iter)            break;         end % % %         Scattering stages         F=abs((fitness(i)-GBest_fitness)/(GBest_fitness-(in1(NoF_LightRays)))); %  "equation (25)"          if F<rand || rand<Ps             if rand<Pe                   NewWLightRays(i,:)=(LightRays(i,:))+(rand)*(LightRays(randi(NoF_LightRays),:)-LightRays(randi(NoF_LightRays),:))+(rand<B).*rand(1,dim).*((GBestRayColor - LightRays(i,:))); %  "equation (21)"              else                             NewWLightRays(i,:)=(((2*cos(rand*180)).*(GBestRayColor.*LightRays(i,:))));   % "equation (22)"             end         else             U=(rand(1,dim)>rand(1,dim));             NewWLightRays(i,:)= U.*(LightRays(randi(NoF_LightRays),:)+abs(randn).*(LightRays(randi(NoF_LightRays),:)-LightRays(randi(NoF_LightRays),:)))+(1-U).*LightRays(i,:);  % "equation (24)"         end          % % % check bound limitation           if rand<Ph                U=NewWLightRays(i,:)>ub;                L=NewWLightRays(i,:)<lb;                NewWLightRays(i,:)=(NewWLightRays(i,:).*(~(U+L)))+ub.*U+lb.*L;         else             for j=1:size(LightRays,2)             if  NewWLightRays(i,j)>ub(j)                 NewWLightRays(i,j)=lb(j)+rand*(ub(j)-lb(j));             elseif  NewWLightRays(i,j)<lb(j)                 NewWLightRays(i,j)=lb(j)+rand*(ub(j)-lb(j));             end             end          end      % Calculate objective function for each search agent      Fnew=fobj(NewWLightRays(i,:));      % If fitness improves (better solutions found), update then      if (Fnew<=fitness(i)),           LightRays(i,:)=NewWLightRays(i,:);           fitness(i)=Fnew;       end      %% update Global best solution       if  Fnew<=GBest_fitness           GBestRayColor=NewWLightRays(i,:);    % Update Global best solution           GBest_fitness=Fnew;       end       Conv_curve(it)=GBest_fitness;       it=it+1;       if (it>Max_iter)         break;       end     end  %% end i  end %% End the optimization process end

参考文献

[1] Abdel-Basset M, Mohamed R, Sallam K M, et al. Light spectrum optimizer: a novel physics-inspired metaheuristic optimization algorithm[J]. Mathematics, 2022, 10(19): 3466.

完整代码获取方式：后台回复关键字：

TGDM199