阶跃函数（阶跃信号）

大家好，欢迎来到IT知识分享网。

阶跃函数

阶跃函数可以表示为

$f(t)=\left\{\begin{matrix} 0,\; \; \; \; t<0\\ R,\; \; \; \; t\geq 0 \end{matrix}\right.$

更一般的形式，称为“延时的阶跃函数”：

$f(t-t_{0})=\left\{\begin{matrix} 0,\; \; \; \; t<t_{0}\\ R,\; \; \; \; t\geq t_{0} \end{matrix}\right.$

单位阶跃函数

单位阶跃函数用符号 $\varepsilon (t)$ 表示，有的地方也用 1(t) 、或 u(t) 表示：

$1(t)=u(t)=\varepsilon (t)=\left\{\begin{matrix} 0,\; \; \; \; t<0\\ 1,\; \; \; \; t\geq 0 \end{matrix}\right.$

在跳变点 t=0 处，函数值未定义，或在 t=0 处规定函数值 $u(0)=\frac{1}{2}$ 。

单位阶跃函数的波形为

单位阶跃函数的物理背景是，在 t=0 时刻对某一电路接入单位电源（可以是直流电压源或直流电流源），并且无限持续下去。

容易证明，单位斜变函数的导数等于单位阶跃函数。

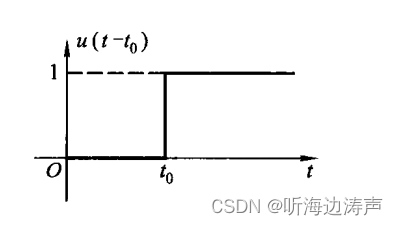
延时的单位阶跃函数

更一般的形式，称为“延时的单位阶跃函数”：

$1(t-t_{0})=u(t-t_{0})=\varepsilon (t-t_{0})=\left\{\begin{matrix} 0,\; \; \; \; t<t_{0}\\ 1,\; \; \; \; t\geq t_{0} \end{matrix}\right.$

波形为

用阶跃信号表示其它信号的接入特性

阶跃信号鲜明地表现出信号的单边特性，即信号在某接入时刻 $t_{0}$ 以前的幅度为零。利用阶跃信号这一特性，可以方便地以数学方式描述各种信号的接入特性。

例如： $f_{1}(t)=(\sin t)u(t)$ 的波形为

$f_{2}(t)=e^{-t}[u(t)-u(t-t_{0})]$ 的波形为

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/129383.html

阶跃函数（阶跃信号）

阶跃函数

单位阶跃函数

延时的单位阶跃函数

用阶跃信号表示其它信号的接入特性

相关推荐

发表回复